Multi-Robot Adversarial Patrolling: Facing a Full-Knowledge Opponent
Paper and Code
Jan 16, 2014
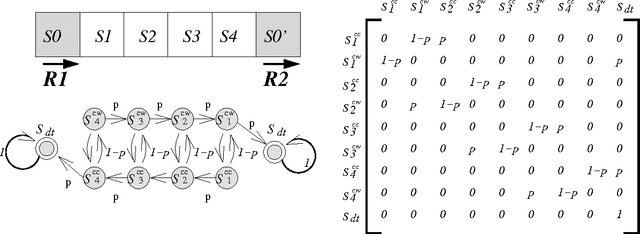
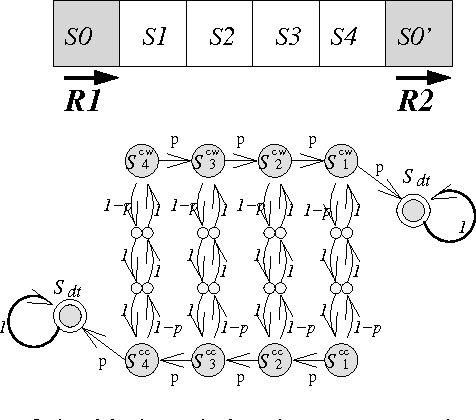
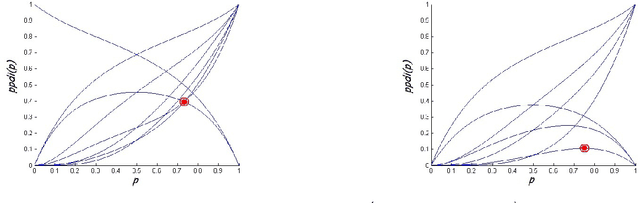
The problem of adversarial multi-robot patrol has gained interest in recent years, mainly due to its immediate relevance to various security applications. In this problem, robots are required to repeatedly visit a target area in a way that maximizes their chances of detecting an adversary trying to penetrate through the patrol path. When facing a strong adversary that knows the patrol strategy of the robots, if the robots use a deterministic patrol algorithm, then in many cases it is easy for the adversary to penetrate undetected (in fact, in some of those cases the adversary can guarantee penetration). Therefore this paper presents a non-deterministic patrol framework for the robots. Assuming that the strong adversary will take advantage of its knowledge and try to penetrate through the patrols weakest spot, hence an optimal algorithm is one that maximizes the chances of detection in that point. We therefore present a polynomial-time algorithm for determining an optimal patrol under the Markovian strategy assumption for the robots, such that the probability of detecting the adversary in the patrols weakest spot is maximized. We build upon this framework and describe an optimal patrol strategy for several robotic models based on their movement abilities (directed or undirected) and sensing abilities (perfect or imperfect), and in different environment models - either patrol around a perimeter (closed polygon) or an open fence (open polyline).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge