Uncertainty with UAV Search of Multiple Goal-oriented Targets

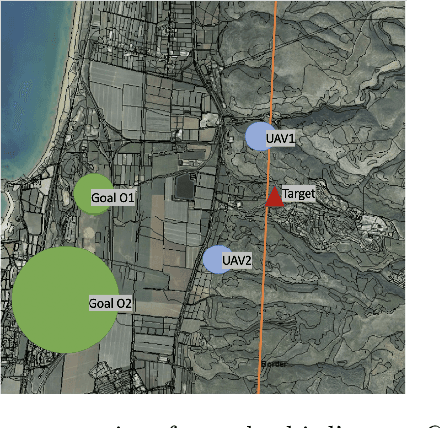
This paper considers the complex problem of a team of UAVs searching targets under uncertainty. The goal of the UAV team is to find all of the moving targets as quickly as possible before they arrive at their selected goal. The uncertainty considered is threefold: First, the UAVs do not know the targets' locations and destinations. Second, the sensing capabilities of the UAVs are not perfect. Third, the targets' movement model is unknown. We suggest a real-time algorithmic framework for the UAVs, combining entropy and stochastic-temporal belief, that aims at optimizing the probability of a quick and successful detection of all of the targets. We have empirically evaluated the algorithmic framework, and have shown its efficiency and significant performance improvement compared to other solutions. Furthermore, we have evaluated our framework using Peer Designed Agents (PDAs), which are computer agents that simulate targets and show that our algorithmic framework outperforms other solutions in this scenario.

Explicit Gradient Learning

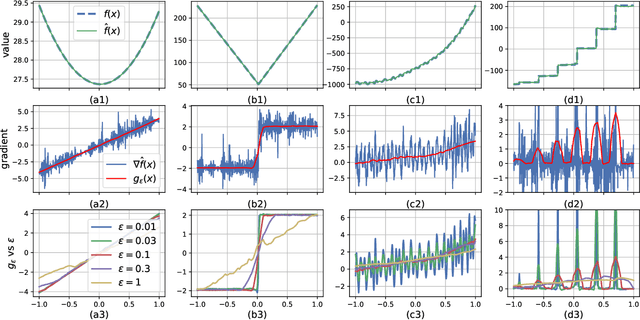
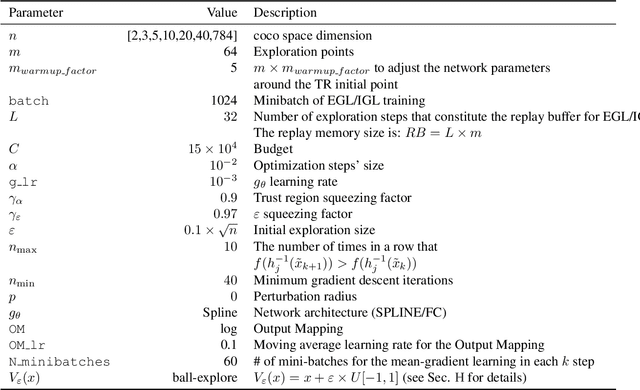
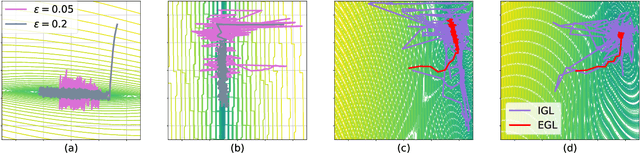
Black-Box Optimization (BBO) methods can find optimal policies for systems that interact with complex environments with no analytical representation. As such, they are of interest in many Artificial Intelligence (AI) domains. Yet classical BBO methods fall short in high-dimensional non-convex problems. They are thus often overlooked in real-world AI tasks. Here we present a BBO method, termed Explicit Gradient Learning (EGL), that is designed to optimize high-dimensional ill-behaved functions. We derive EGL by finding weak-spots in methods that fit the objective function with a parametric Neural Network (NN) model and obtain the gradient signal by calculating the parametric gradient. Instead of fitting the function, EGL trains a NN to estimate the objective gradient directly. We prove the convergence of EGL in convex optimization and its robustness in the optimization of integrable functions. We evaluate EGL and achieve state-of-the-art results in two challenging problems: (1) the COCO test suite against an assortment of standard BBO methods; and (2) in a high-dimensional non-convex image generation task.

Multi-Robot Adversarial Patrolling: Facing a Full-Knowledge Opponent

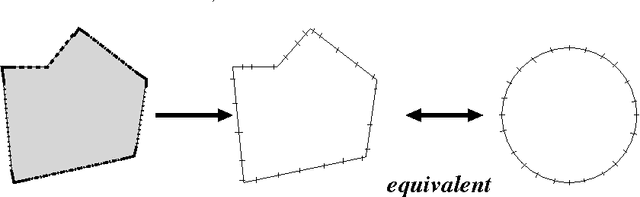
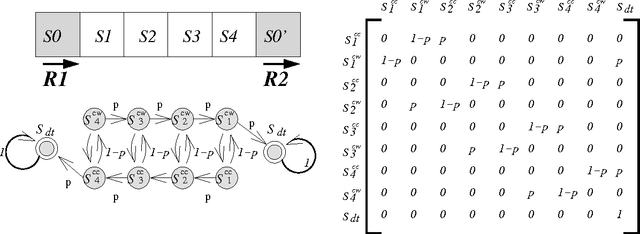
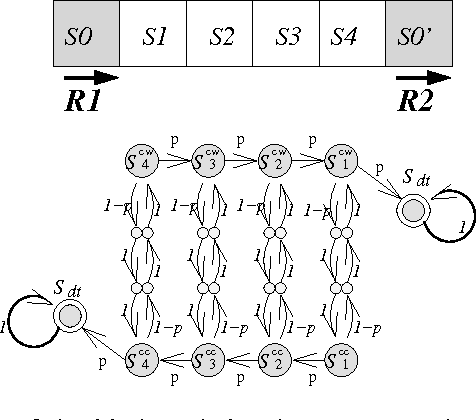
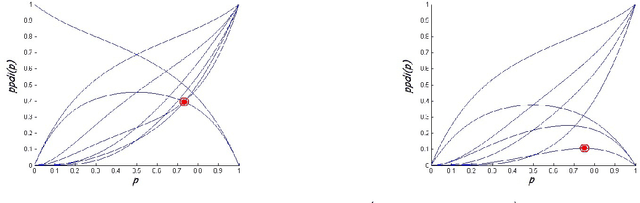
The problem of adversarial multi-robot patrol has gained interest in recent years, mainly due to its immediate relevance to various security applications. In this problem, robots are required to repeatedly visit a target area in a way that maximizes their chances of detecting an adversary trying to penetrate through the patrol path. When facing a strong adversary that knows the patrol strategy of the robots, if the robots use a deterministic patrol algorithm, then in many cases it is easy for the adversary to penetrate undetected (in fact, in some of those cases the adversary can guarantee penetration). Therefore this paper presents a non-deterministic patrol framework for the robots. Assuming that the strong adversary will take advantage of its knowledge and try to penetrate through the patrols weakest spot, hence an optimal algorithm is one that maximizes the chances of detection in that point. We therefore present a polynomial-time algorithm for determining an optimal patrol under the Markovian strategy assumption for the robots, such that the probability of detecting the adversary in the patrols weakest spot is maximized. We build upon this framework and describe an optimal patrol strategy for several robotic models based on their movement abilities (directed or undirected) and sensing abilities (perfect or imperfect), and in different environment models - either patrol around a perimeter (closed polygon) or an open fence (open polyline).