Yoram Louzoun
Optimistic Gradient Learning with Hessian Corrections for High-Dimensional Black-Box Optimization
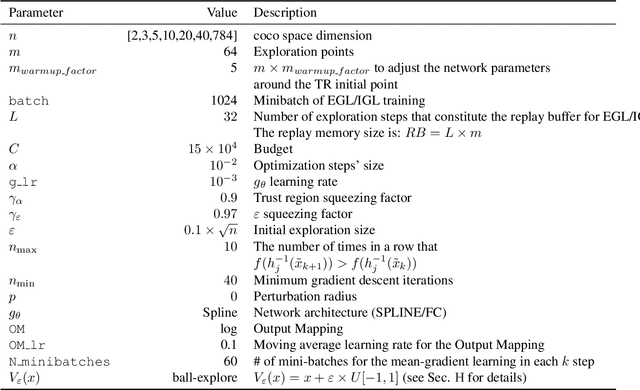
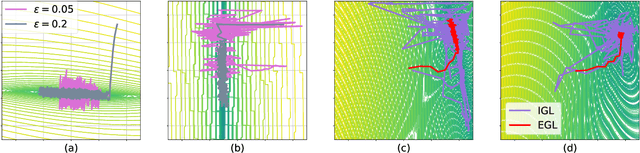
Feb 07, 2025Abstract:Black-box algorithms are designed to optimize functions without relying on their underlying analytical structure or gradient information, making them essential when gradients are inaccessible or difficult to compute. Traditional methods for solving black-box optimization (BBO) problems predominantly rely on non-parametric models and struggle to scale to large input spaces. Conversely, parametric methods that model the function with neural estimators and obtain gradient signals via backpropagation may suffer from significant gradient errors. A recent alternative, Explicit Gradient Learning (EGL), which directly learns the gradient using a first-order Taylor approximation, has demonstrated superior performance over both parametric and non-parametric methods. In this work, we propose two novel gradient learning variants to address the robustness challenges posed by high-dimensional, complex, and highly non-linear problems. Optimistic Gradient Learning (OGL) introduces a bias toward lower regions in the function landscape, while Higher-order Gradient Learning (HGL) incorporates second-order Taylor corrections to improve gradient accuracy. We combine these approaches into the unified OHGL algorithm, achieving state-of-the-art (SOTA) performance on the synthetic COCO suite. Additionally, we demonstrate OHGLs applicability to high-dimensional real-world machine learning (ML) tasks such as adversarial training and code generation. Our results highlight OHGLs ability to generate stronger candidates, offering a valuable tool for ML researchers and practitioners tackling high-dimensional, non-linear optimization challenges
Data-driven Coreference-based Ontology Building
Oct 22, 2024Abstract:While coreference resolution is traditionally used as a component in individual document understanding, in this work we take a more global view and explore what can we learn about a domain from the set of all document-level coreference relations that are present in a large corpus. We derive coreference chains from a corpus of 30 million biomedical abstracts and construct a graph based on the string phrases within these chains, establishing connections between phrases if they co-occur within the same coreference chain. We then use the graph structure and the betweeness centrality measure to distinguish between edges denoting hierarchy, identity and noise, assign directionality to edges denoting hierarchy, and split nodes (strings) that correspond to multiple distinct concepts. The result is a rich, data-driven ontology over concepts in the biomedical domain, parts of which overlaps significantly with human-authored ontologies. We release the coreference chains and resulting ontology under a creative-commons license, along with the code.
Planted Dense Subgraphs in Dense Random Graphs Can Be Recovered using Graph-based Machine Learning
Jan 05, 2022



Abstract:Multiple methods of finding the vertices belonging to a planted dense subgraph in a random dense $G(n, p)$ graph have been proposed, with an emphasis on planted cliques. Such methods can identify the planted subgraph in polynomial time, but are all limited to several subgraph structures. Here, we present PYGON, a graph neural network-based algorithm, which is insensitive to the structure of the planted subgraph. This is the first algorithm that uses advanced learning tools for recovering dense subgraphs. We show that PYGON can recover cliques of sizes $\Theta\left(\sqrt{n}\right)$, where $n$ is the size of the background graph, comparable with the state of the art. We also show that the same algorithm can recover multiple other planted subgraphs of size $\Theta\left(\sqrt{n}\right)$, in both directed and undirected graphs. We suggest a conjecture that no polynomial time PAC-learning algorithm can detect planted dense subgraphs with size smaller than $O\left(\sqrt{n}\right)$, even if in principle one could find dense subgraphs of logarithmic size.
Quadratic GCN for Graph Classification
Apr 14, 2021



Abstract:Graph Convolutional Networks (GCNs) have been extensively used to classify vertices in graphs and have been shown to outperform other vertex classification methods. GCNs have been extended to graph classification tasks (GCT). In GCT, graphs with different numbers of edges and vertices belong to different classes, and one attempts to predict the graph class. GCN based GCT have mostly used pooling and attention-based models. The accuracy of existing GCT methods is still limited. We here propose a novel solution combining GCN, methods from knowledge graphs, and a new self-regularized activation function to significantly improve the accuracy of the GCN based GCT. We present quadratic GCN (QGCN) - A GCN formalism with a quadratic layer. Such a layer produces an output with fixed dimensions, independent of the graph vertex number. We applied this method to a wide range of graph classification problems, and show that when using a self regularized activation function, QGCN outperforms the state of the art methods for all graph classification tasks tested with or without external input on each graph. The code for QGCN is available at: https://github.com/Unknown-Data/QGCN .
Explicit Gradient Learning
Jun 09, 2020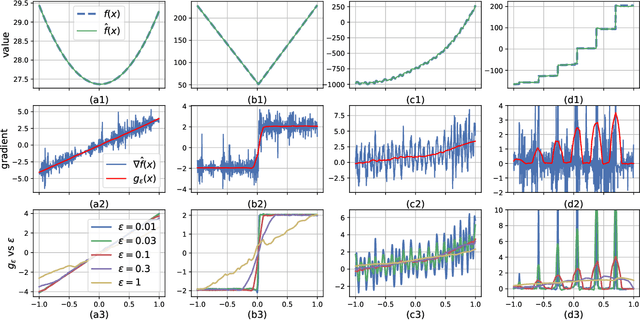

Abstract:Black-Box Optimization (BBO) methods can find optimal policies for systems that interact with complex environments with no analytical representation. As such, they are of interest in many Artificial Intelligence (AI) domains. Yet classical BBO methods fall short in high-dimensional non-convex problems. They are thus often overlooked in real-world AI tasks. Here we present a BBO method, termed Explicit Gradient Learning (EGL), that is designed to optimize high-dimensional ill-behaved functions. We derive EGL by finding weak-spots in methods that fit the objective function with a parametric Neural Network (NN) model and obtain the gradient signal by calculating the parametric gradient. Instead of fitting the function, EGL trains a NN to estimate the objective gradient directly. We prove the convergence of EGL in convex optimization and its robustness in the optimization of integrable functions. We evaluate EGL and achieve state-of-the-art results in two challenging problems: (1) the COCO test suite against an assortment of standard BBO methods; and (2) in a high-dimensional non-convex image generation task.
Topological based classification using graph convolutional networks
Oct 26, 2019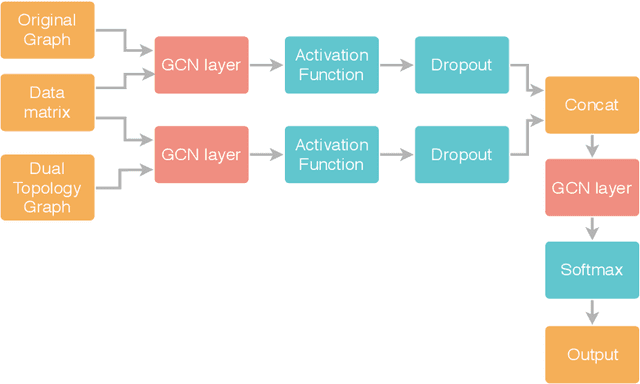
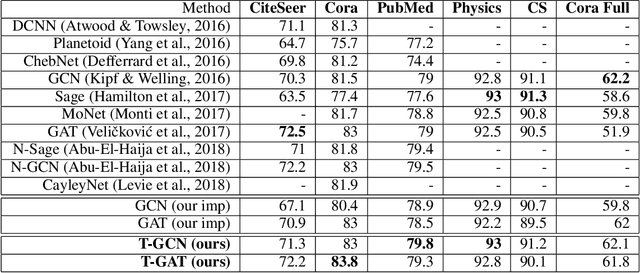
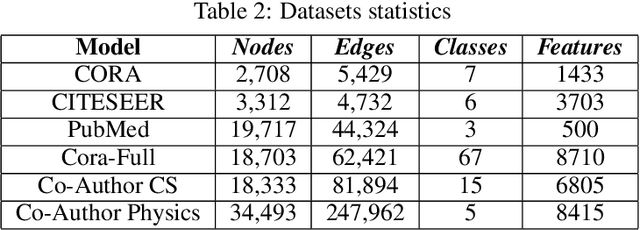
Abstract:In colored graphs, node classes are often associated with either their neighbors class or with information not incorporated in the graph associated with each node. We here propose that node classes are also associated with topological features of the nodes. We use this association to improve Graph machine learning in general and specifically, Graph Convolutional Networks (GCN). First, we show that even in the absence of any external information on nodes, a good accuracy can be obtained on the prediction of the node class using either topological features, or using the neighbors class as an input to a GCN. This accuracy is slightly less than the one that can be obtained using content based GCN. Secondly, we show that explicitly adding the topology as an input to the GCN does not improve the accuracy when combined with external information on nodes. However, adding an additional adjacency matrix with edges between distant nodes with similar topology to the GCN does significantly improve its accuracy, leading to results better than all state of the art methods in multiple datasets.
Regional based query in graph active learning
Jun 20, 2019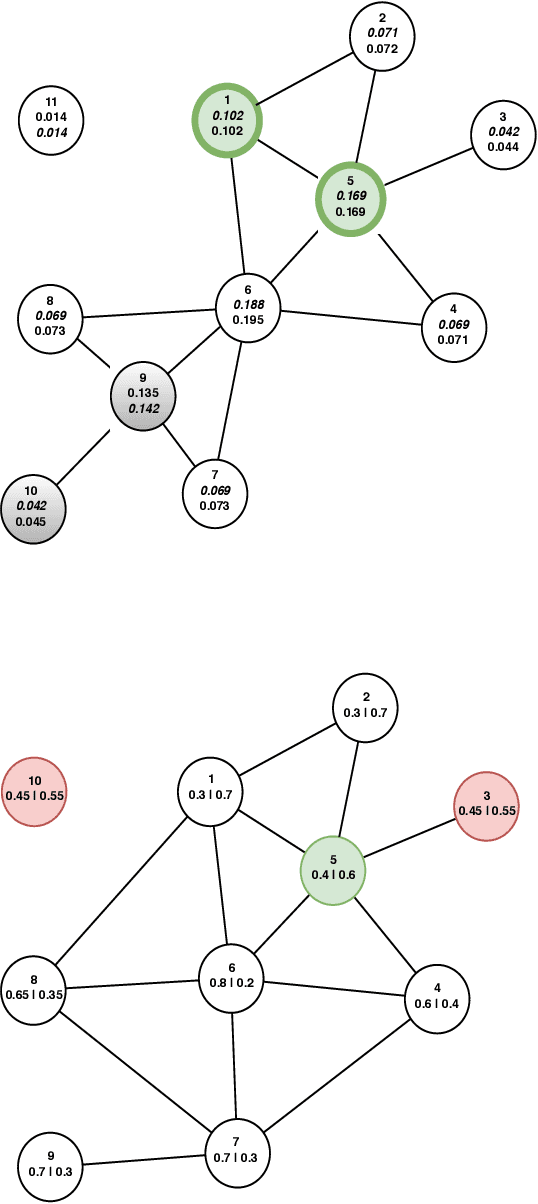
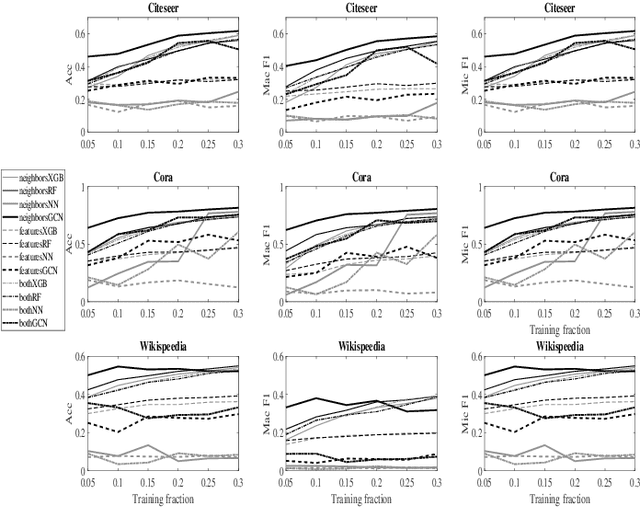
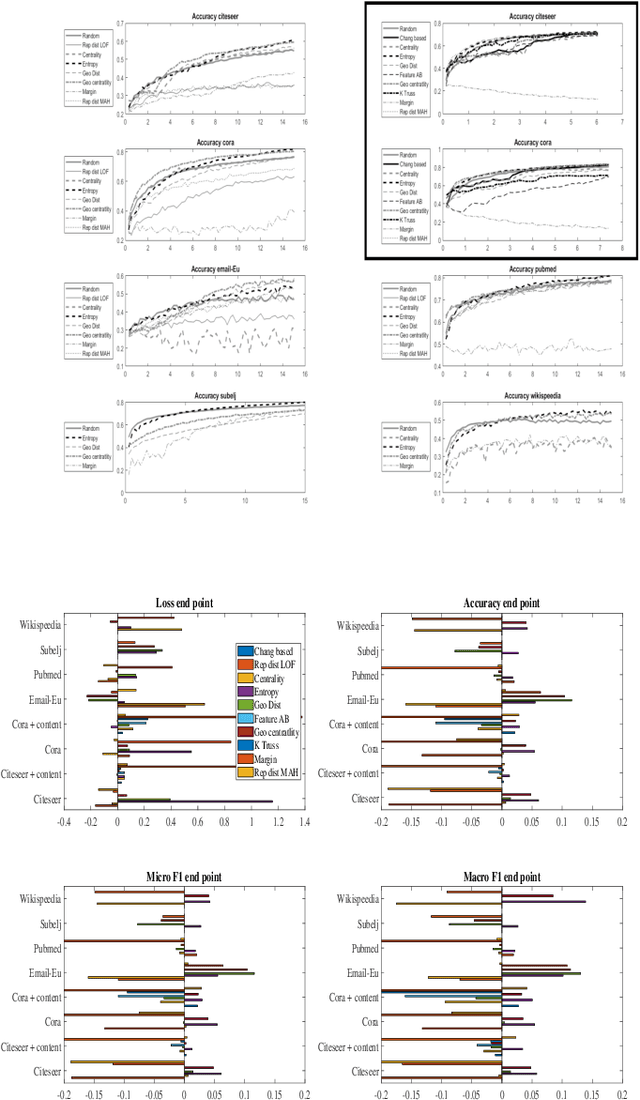
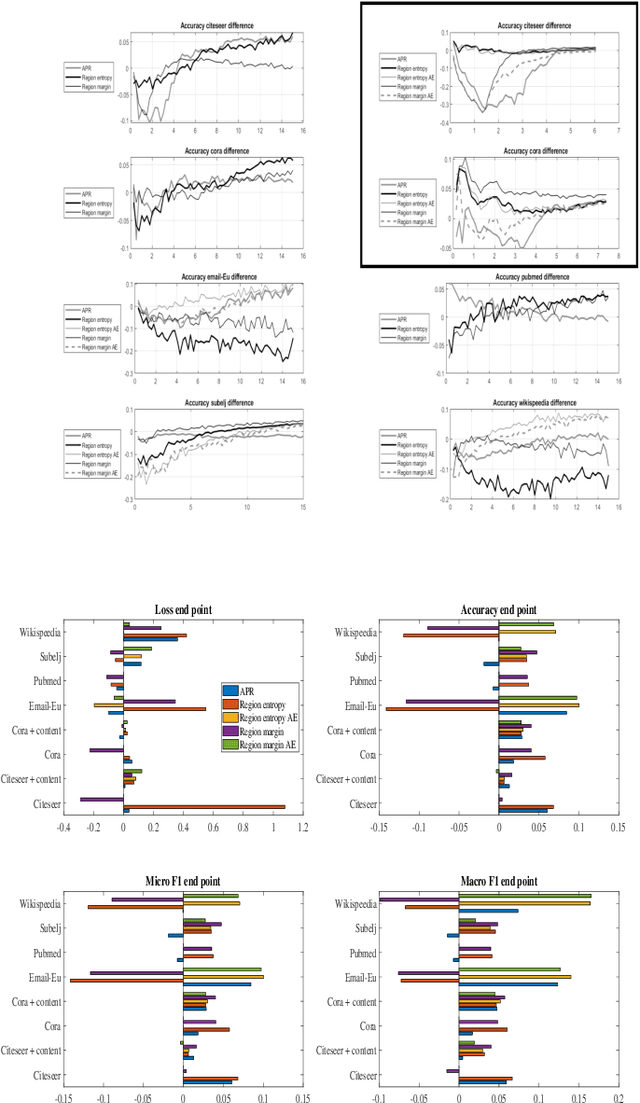
Abstract:Graph convolution networks (GCN) have emerged as the leading method to classify node classes in networks, and have reached the highest accuracy in multiple node classification tasks. In the absence of available tagged samples, active learning methods have been developed to obtain the highest accuracy using the minimal number of queries to an oracle. The current best active learning methods use the sample class uncertainty as selection criteria. However, in graph based classification, the class of each node is often related to the class of its neighbors. As such, the uncertainty in the class of a node's neighbor may be a more appropriate selection criterion. We here propose two such criteria, one extending the classical uncertainty measure, and the other extending the page-rank algorithm. We show that the latter is optimal when the fraction of tagged nodes is low, and when this fraction grows to one over the average degree, the regional uncertainty performs better than all existing methods. While we have tested this methods on graphs, such methods can be extended to any classification problem, where a distance metrics can be defined between the input samples. All the code used can be accessed at : https://github.com/louzounlab/graph-al All the datasets used can be accessed at : https://github.com/louzounlab/DataSets
Topological based classification of paper domains using graph convolutional networks
Apr 10, 2019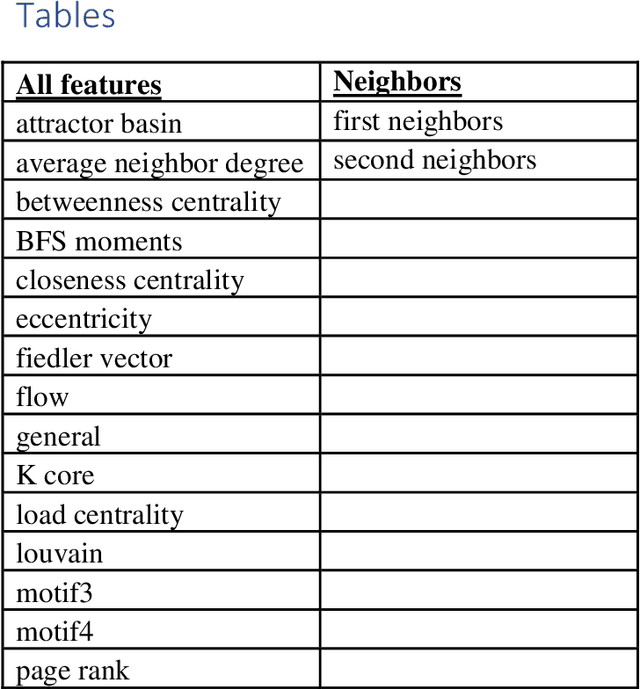
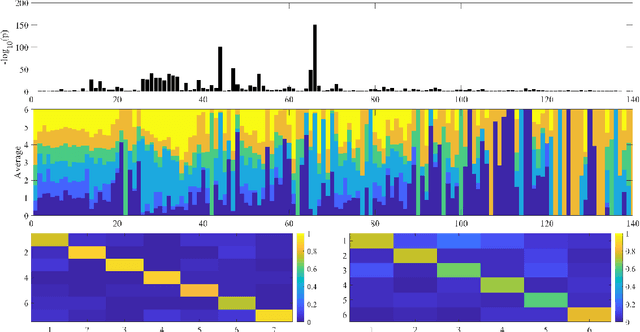
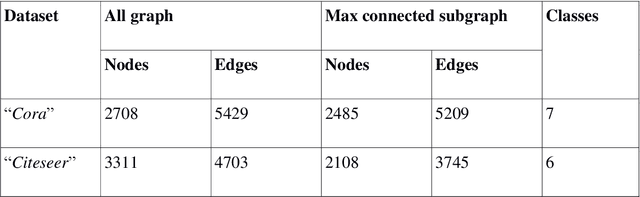
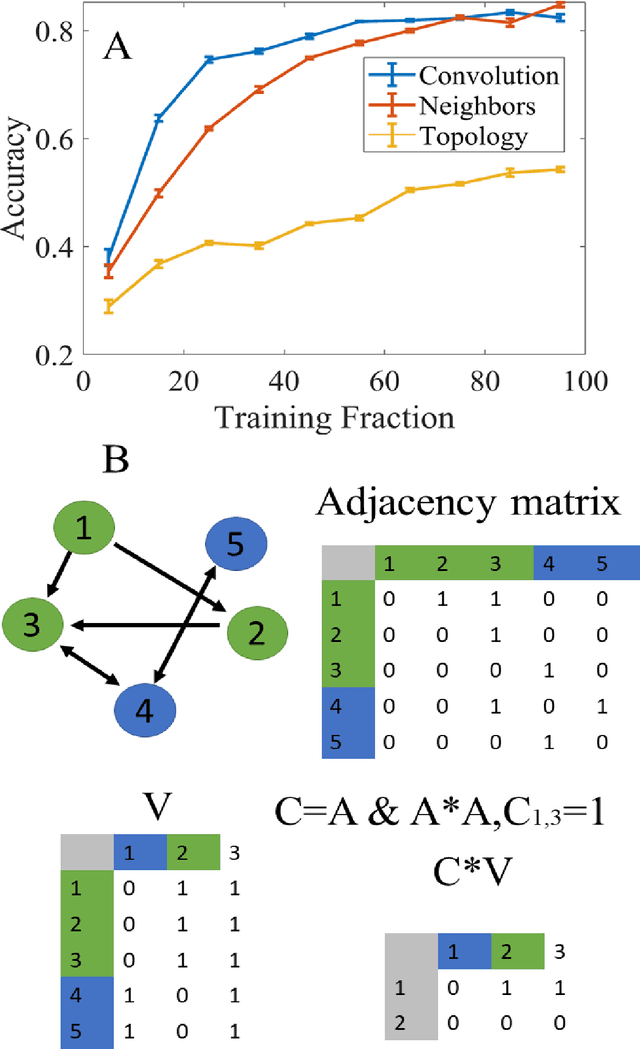
Abstract:The main approaches for node classification in graphs are information propagation and the association of the class of the node with external information. State of the art methods merge these approaches through Graph Convolutional Networks. We here use the association of topological features of the nodes with their class to predict this class. Moreover, combining topological information with information propagation improves classification accuracy on the standard CiteSeer and Cora paper classification task. Topological features and information propagation produce results almost as good as text-based classification, without no textual or content information. We propose to represent the topology and information propagation through a GCN with the neighboring training node classification as an input and the current node classification as output. Such a formalism outperforms state of the art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge