Topological based classification using graph convolutional networks

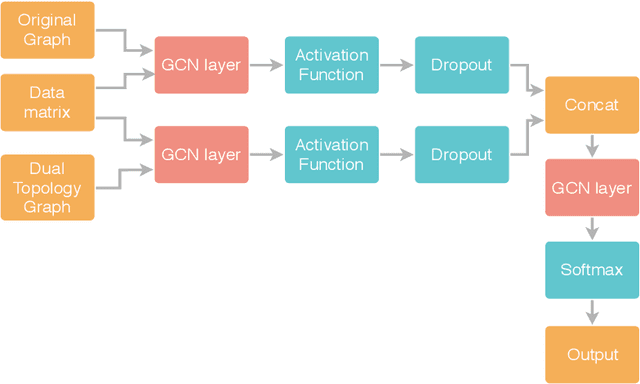
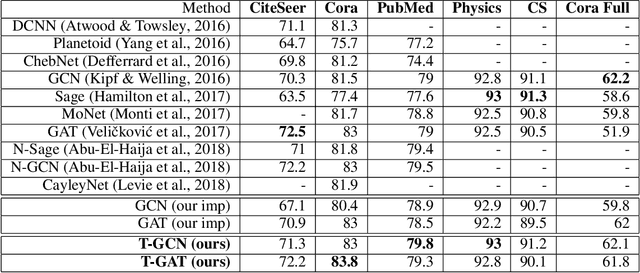
In colored graphs, node classes are often associated with either their neighbors class or with information not incorporated in the graph associated with each node. We here propose that node classes are also associated with topological features of the nodes. We use this association to improve Graph machine learning in general and specifically, Graph Convolutional Networks (GCN). First, we show that even in the absence of any external information on nodes, a good accuracy can be obtained on the prediction of the node class using either topological features, or using the neighbors class as an input to a GCN. This accuracy is slightly less than the one that can be obtained using content based GCN. Secondly, we show that explicitly adding the topology as an input to the GCN does not improve the accuracy when combined with external information on nodes. However, adding an additional adjacency matrix with edges between distant nodes with similar topology to the GCN does significantly improve its accuracy, leading to results better than all state of the art methods in multiple datasets.

Topological based classification of paper domains using graph convolutional networks

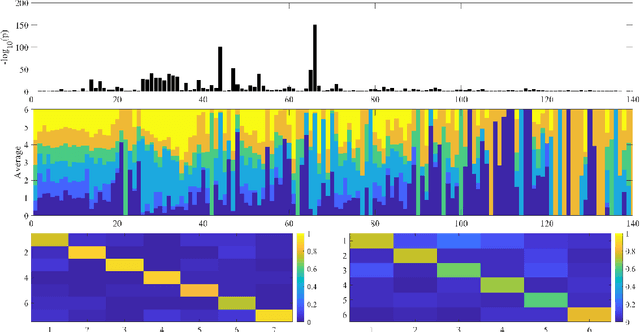
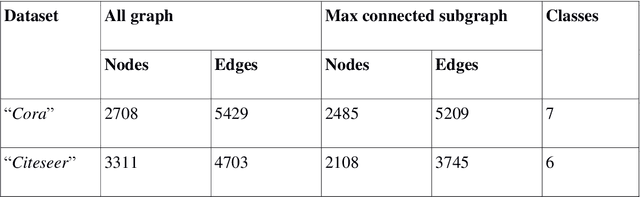
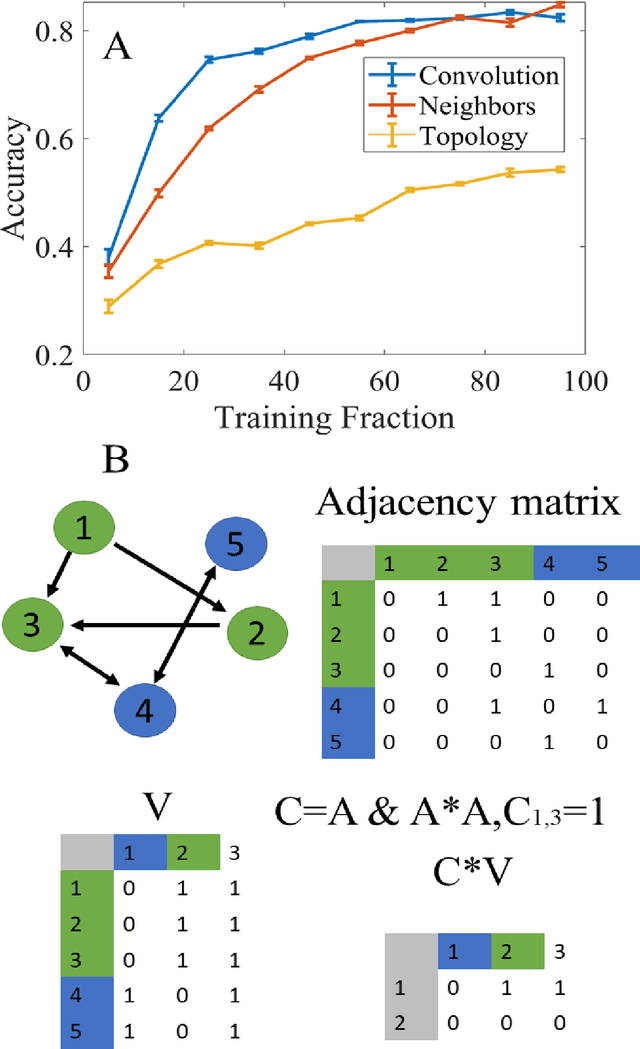
The main approaches for node classification in graphs are information propagation and the association of the class of the node with external information. State of the art methods merge these approaches through Graph Convolutional Networks. We here use the association of topological features of the nodes with their class to predict this class. Moreover, combining topological information with information propagation improves classification accuracy on the standard CiteSeer and Cora paper classification task. Topological features and information propagation produce results almost as good as text-based classification, without no textual or content information. We propose to represent the topology and information propagation through a GCN with the neighboring training node classification as an input and the current node classification as output. Such a formalism outperforms state of the art methods.