Multi-Agent Path Finding with Deadlines: Preliminary Results
Paper and Code
May 13, 2018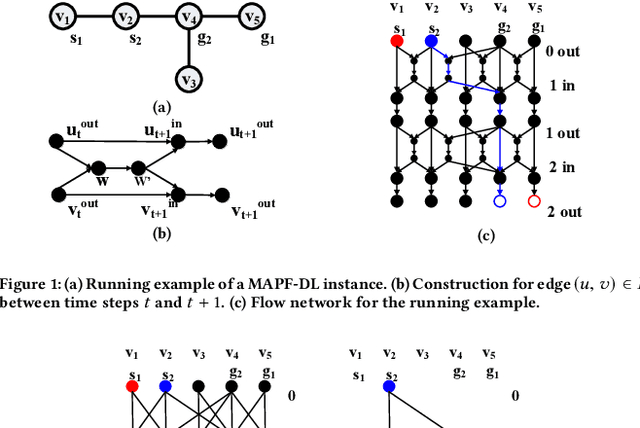
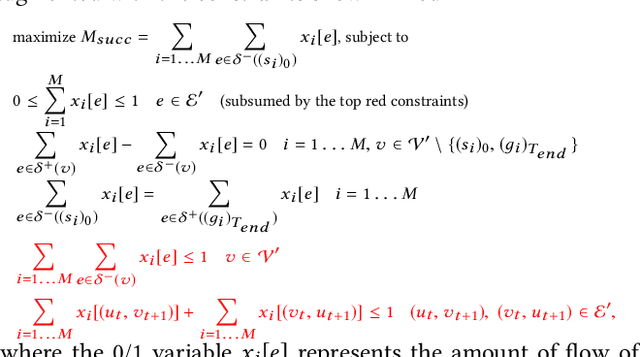
We formalize the problem of multi-agent path finding with deadlines (MAPF-DL). The objective is to maximize the number of agents that can reach their given goal vertices from their given start vertices within a given deadline, without colliding with each other. We first show that the MAPF-DL problem is NP-hard to solve optimally. We then present an optimal MAPF-DL algorithm based on a reduction of the MAPF-DL problem to a flow problem and a subsequent compact integer linear programming formulation of the resulting reduced abstracted multi-commodity flow network.
* AAMAS 2018, to appear
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge