A Unifying View of Linear Function Approximation in Off-Policy RL Through Matrix Splitting and Preconditioning

Traditionally, TD and FQI are viewed as differing in the number of updates toward the target value function: TD makes one update, FQI makes an infinite number, and Partial Fitted Q-Iteration (PFQI) performs a finite number, such as the use of a target network in Deep Q-Networks (DQN) in the OPE setting. This perspective, however, fails to capture the convergence connections between these algorithms and may lead to incorrect conclusions, for example, that the convergence of TD implies the convergence of FQI. In this paper, we focus on linear value function approximation and offer a new perspective, unifying TD, FQI, and PFQI as the same iterative method for solving the Least Squares Temporal Difference (LSTD) system, but using different preconditioners and matrix splitting schemes. TD uses a constant preconditioner, FQI employs a data-feature adaptive preconditioner, and PFQI transitions between the two. Then, we reveal that in the context of linear function approximation, increasing the number of updates under the same target value function essentially represents a transition from using a constant preconditioner to data-feature adaptive preconditioner. This unifying perspective also simplifies the analyses of the convergence conditions for these algorithms and clarifies many issues. Consequently, we fully characterize the convergence of each algorithm without assuming specific properties of the chosen features (e.g., linear independence). We also examine how common assumptions about feature representations affect convergence, and discover new conditions on features that are important for convergence. These convergence conditions allow us to establish the convergence connections between these algorithms and to address important questions.

Interpolating Between Softmax Policy Gradient and Neural Replicator Dynamics with Capped Implicit Exploration

Neural replicator dynamics (NeuRD) is an alternative to the foundational softmax policy gradient (SPG) algorithm motivated by online learning and evolutionary game theory. The NeuRD expected update is designed to be nearly identical to that of SPG, however, we show that the Monte Carlo updates differ in a substantial way: the importance correction accounting for a sampled action is nullified in the SPG update, but not in the NeuRD update. Naturally, this causes the NeuRD update to have higher variance than its SPG counterpart. Building on implicit exploration algorithms in the adversarial bandit setting, we introduce capped implicit exploration (CIX) estimates that allow us to construct NeuRD-CIX, which interpolates between this aspect of NeuRD and SPG. We show how CIX estimates can be used in a black-box reduction to construct bandit algorithms with regret bounds that hold with high probability and the benefits this entails for NeuRD-CIX in sequential decision-making settings. Our analysis reveals a bias--variance tradeoff between SPG and NeuRD, and shows how theory predicts that NeuRD-CIX will perform well more consistently than NeuRD while retaining NeuRD's advantages over SPG in non-stationary environments.

Robust No-Regret Learning in Min-Max Stackelberg Games

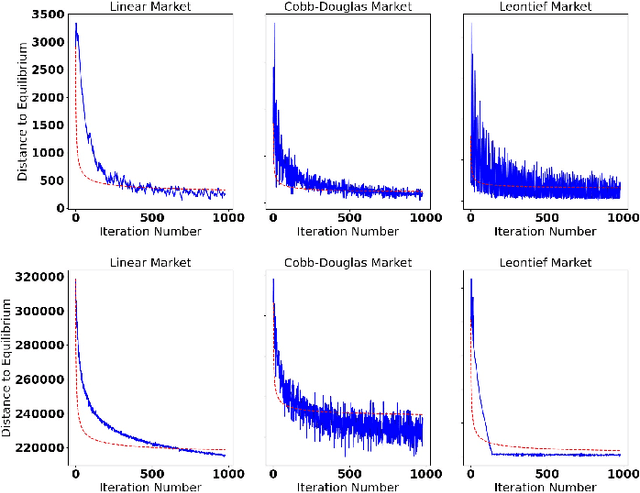
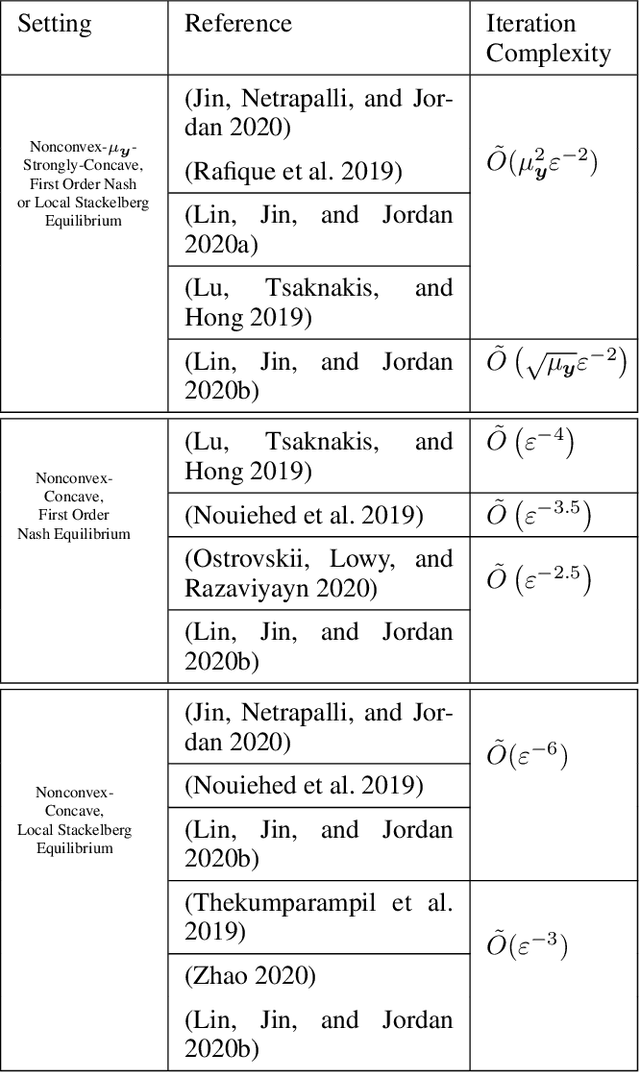
The behavior of no-regret learning algorithms is well understood in two-player min-max (i.e, zero-sum) games. In this paper, we investigate the behavior of no-regret learning in min-max games with dependent strategy sets, where the strategy of the first player constrains the behavior of the second. Such games are best understood as sequential, i.e., min-max Stackelberg, games. We consider two settings, one in which only the first player chooses their actions using a no-regret algorithm while the second player best responds, and one in which both players use no-regret algorithms. For the former case, we show that no-regret dynamics converge to a Stackelberg equilibrium. For the latter case, we introduce a new type of regret, which we call Lagrangian regret, and show that if both players minimize their Lagrangian regrets, then play converges to a Stackelberg equilibrium. We then observe that online mirror descent (OMD) dynamics in these two settings correspond respectively to a known nested (i.e., sequential) gradient descent-ascent (GDA) algorithm and a new simultaneous GDA-like algorithm, thereby establishing convergence of these algorithms to Stackelberg equilibrium. Finally, we analyze the robustness of OMD dynamics to perturbations by investigating online min-max Stackelberg games. We prove that OMD dynamics are robust for a large class of online min-max games with independent strategy sets. In the dependent case, we demonstrate the robustness of OMD dynamics experimentally by simulating them in online Fisher markets, a canonical example of a min-max Stackelberg game with dependent strategy sets.

Convex-Concave Min-Max Stackelberg Games

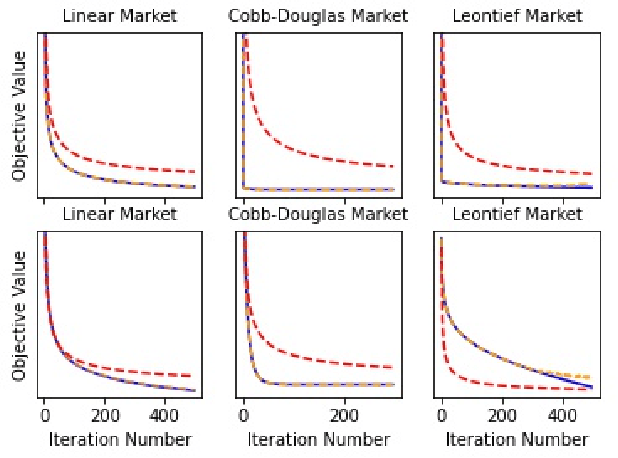
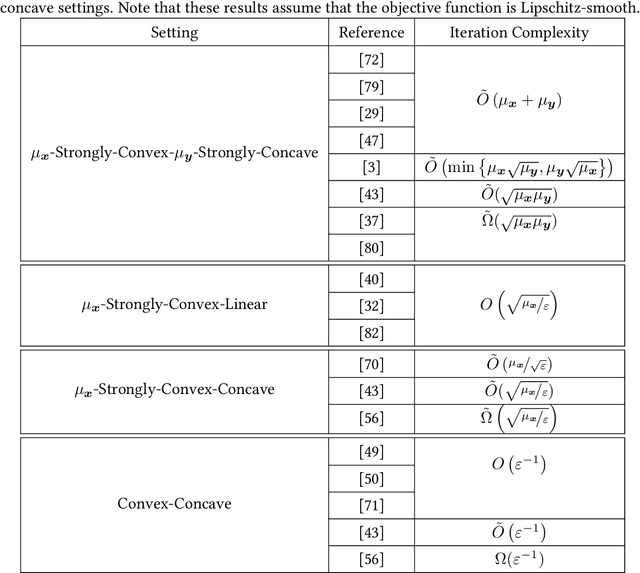
Min-max optimization problems (i.e., min-max games) have been attracting a great deal of attention because of their applicability to a wide range of machine learning problems. Although significant progress has been made recently, the literature to date has focused on games with independent strategy sets; little is known about solving games with dependent strategy sets, which can be characterized as min-max Stackelberg games. We introduce two first-order methods that solve a large class of convex-concave min-max Stackelberg games, and show that our methods converge in polynomial time. Min-max Stackelberg games were first studied by Wald, under the posthumous name of Wald's maximin model, a variant of which is the main paradigm used in robust optimization, which means that our methods can likewise solve many convex robust optimization problems. We observe that the computation of competitive equilibria in Fisher markets also comprises a min-max Stackelberg game. Further, we demonstrate the efficacy and efficiency of our algorithms in practice by computing competitive equilibria in Fisher markets with varying utility structures. Our experiments suggest potential ways to extend our theoretical results, by demonstrating how different smoothness properties can affect the convergence rate of our algorithms.

Efficient Deviation Types and Learning for Hindsight Rationality in Extensive-Form Games

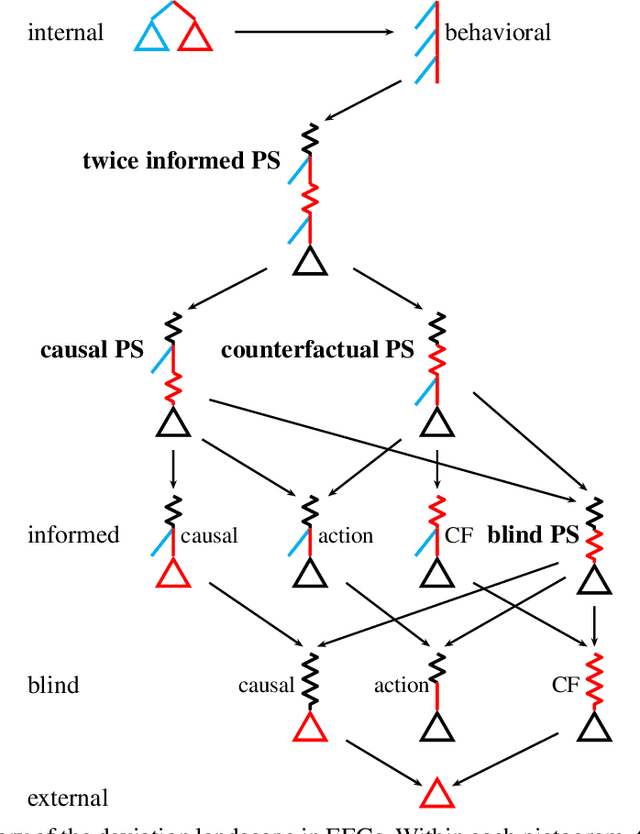
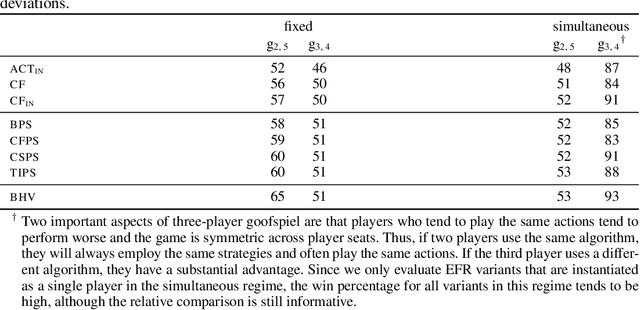
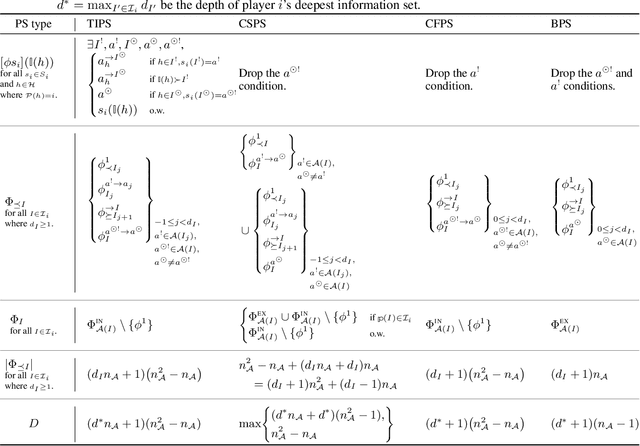
Hindsight rationality is an approach to playing multi-agent, general-sum games that prescribes no-regret learning dynamics and describes jointly rational behavior with mediated equilibria. We explore the space of deviation types in extensive-form games (EFGs) and discover powerful types that are efficient to compute in games with moderate lengths. Specifically, we identify four new types of deviations that subsume previously studied types within a broader class we call partial sequence deviations. Integrating the idea of time selection regret minimization into counterfactual regret minimization (CFR), we introduce the extensive-form regret minimization (EFR) algorithm that is hindsight rational for a general and natural class of deviations in EFGs. We provide instantiations and regret bounds for EFR that correspond to each partial sequence deviation type. In addition, we present a thorough empirical analysis of EFR's performance with different deviation types in common benchmark games. As theory suggests, instantiating EFR with stronger deviations leads to behavior that tends to outperform that of weaker deviations.

Hindsight and Sequential Rationality of Correlated Play

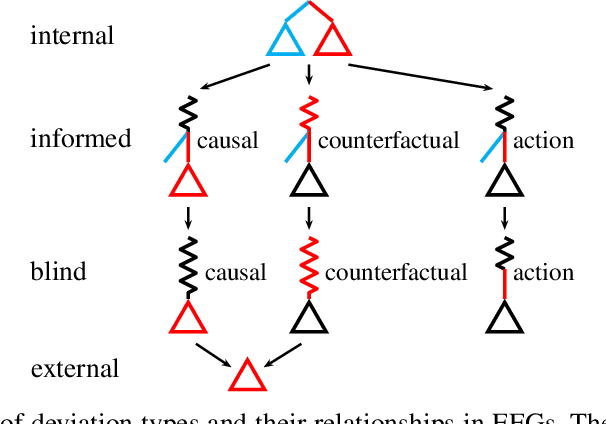
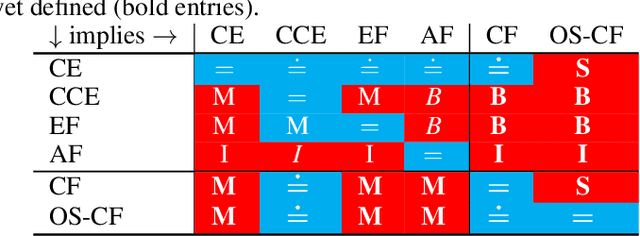
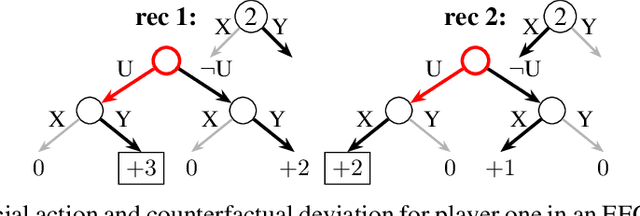
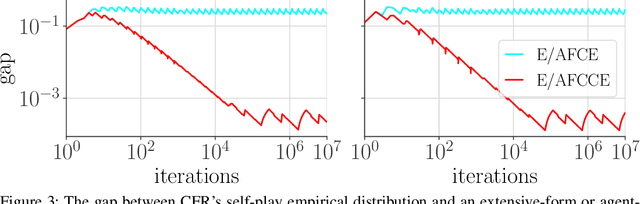
Driven by recent successes in two-player, zero-sum game solving and playing, artificial intelligence work on games has increasingly focused on algorithms that produce equilibrium-based strategies. However, this approach has been less effective at producing competent players in general-sum games or those with more than two players than in two-player, zero-sum games. An appealing alternative is to consider adaptive algorithms that ensure strong performance in hindsight relative to what could have been achieved with modified behavior. This approach also leads to a game-theoretic analysis, but in the correlated play that arises from joint learning dynamics rather than factored agent behavior at equilibrium. We develop and advocate for this hindsight rationality framing of learning in general sequential decision-making settings. To this end, we re-examine mediated equilibrium and deviation types in extensive-form games, thereby gaining a more complete understanding and resolving past misconceptions. We present a set of examples illustrating the distinct strengths and weaknesses of each type of equilibrium in the literature, and prove that no tractable concept subsumes all others. This line of inquiry culminates in the definition of the deviation and equilibrium classes that correspond to algorithms in the counterfactual regret minimization (CFR) family, relating them to all others in the literature. Examining CFR in greater detail further leads to a new recursive definition of rationality in correlated play that extends sequential rationality in a way that naturally applies to hindsight evaluation.

RoxyBot-06: Stochastic Prediction and Optimization in TAC Travel

In this paper, we describe our autonomous bidding agent, RoxyBot, who emerged victorious in the travel division of the 2006 Trading Agent Competition in a photo finish. At a high level, the design of many successful trading agents can be summarized as follows: (i) price prediction: build a model of market prices; and (ii) optimization: solve for an approximately optimal set of bids, given this model. To predict, RoxyBot builds a stochastic model of market prices by simulating simultaneous ascending auctions. To optimize, RoxyBot relies on the sample average approximation method, a stochastic optimization technique.