Convex-Concave Min-Max Stackelberg Games
Paper and Code
Oct 05, 2021
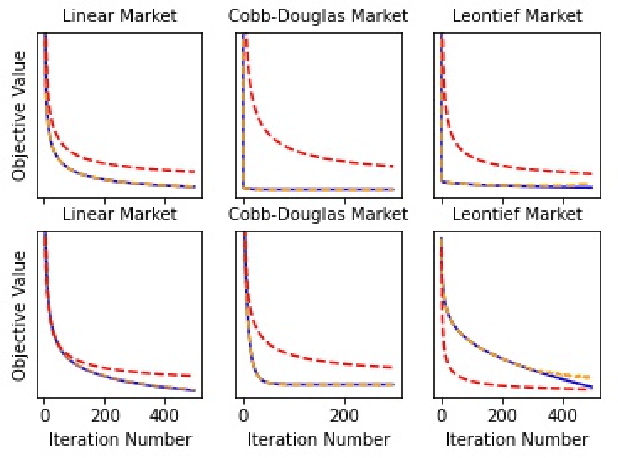

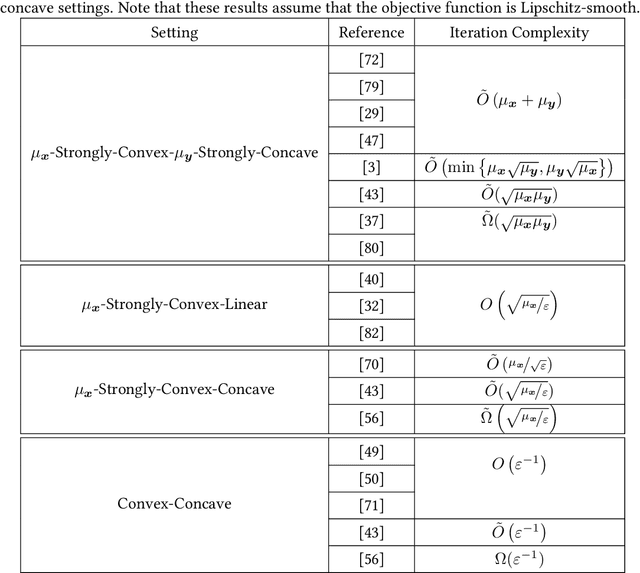
Min-max optimization problems (i.e., min-max games) have been attracting a great deal of attention because of their applicability to a wide range of machine learning problems. Although significant progress has been made recently, the literature to date has focused on games with independent strategy sets; little is known about solving games with dependent strategy sets, which can be characterized as min-max Stackelberg games. We introduce two first-order methods that solve a large class of convex-concave min-max Stackelberg games, and show that our methods converge in polynomial time. Min-max Stackelberg games were first studied by Wald, under the posthumous name of Wald's maximin model, a variant of which is the main paradigm used in robust optimization, which means that our methods can likewise solve many convex robust optimization problems. We observe that the computation of competitive equilibria in Fisher markets also comprises a min-max Stackelberg game. Further, we demonstrate the efficacy and efficiency of our algorithms in practice by computing competitive equilibria in Fisher markets with varying utility structures. Our experiments suggest potential ways to extend our theoretical results, by demonstrating how different smoothness properties can affect the convergence rate of our algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge