Flow-Based Synthesis of Reactive Tests for Discrete Decision-Making Systems with Temporal Logic Specifications

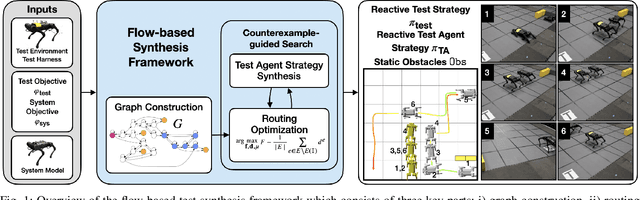
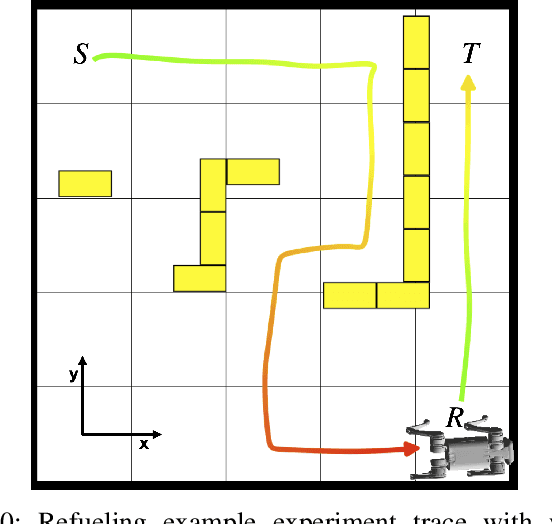
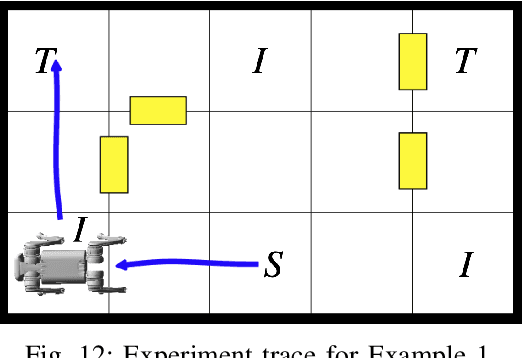
Designing tests to evaluate if a given autonomous system satisfies complex specifications is challenging due to the complexity of these systems. This work proposes a flow-based approach for reactive test synthesis from temporal logic specifications, enabling the synthesis of test environments consisting of static and reactive obstacles and dynamic test agents. The temporal logic specifications describe desired test behavior, including system requirements as well as a test objective that is not revealed to the system. The synthesized test strategy places restrictions on system actions in reaction to the system state. The tests are minimally restrictive and accomplish the test objective while ensuring realizability of the system's objective without aiding it (semi-cooperative setting). Automata theory and flow networks are leveraged to formulate a mixed-integer linear program (MILP) to synthesize the test strategy. For a dynamic test agent, the agent strategy is synthesized for a GR(1) specification constructed from the solution of the MILP. If the specification is unrealizable by the dynamics of the test agent, a counterexample-guided approach is used to resolve the MILP until a strategy is found. This flow-based, reactive test synthesis is conducted offline and is agnostic to the system controller. Finally, the resulting test strategy is demonstrated in simulation and experimentally on a pair of quadrupedal robots for a variety of specifications.

Robust No-Regret Learning in Min-Max Stackelberg Games

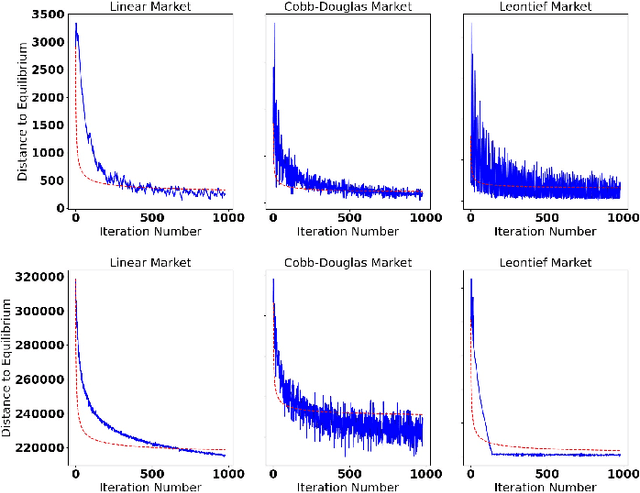
The behavior of no-regret learning algorithms is well understood in two-player min-max (i.e, zero-sum) games. In this paper, we investigate the behavior of no-regret learning in min-max games with dependent strategy sets, where the strategy of the first player constrains the behavior of the second. Such games are best understood as sequential, i.e., min-max Stackelberg, games. We consider two settings, one in which only the first player chooses their actions using a no-regret algorithm while the second player best responds, and one in which both players use no-regret algorithms. For the former case, we show that no-regret dynamics converge to a Stackelberg equilibrium. For the latter case, we introduce a new type of regret, which we call Lagrangian regret, and show that if both players minimize their Lagrangian regrets, then play converges to a Stackelberg equilibrium. We then observe that online mirror descent (OMD) dynamics in these two settings correspond respectively to a known nested (i.e., sequential) gradient descent-ascent (GDA) algorithm and a new simultaneous GDA-like algorithm, thereby establishing convergence of these algorithms to Stackelberg equilibrium. Finally, we analyze the robustness of OMD dynamics to perturbations by investigating online min-max Stackelberg games. We prove that OMD dynamics are robust for a large class of online min-max games with independent strategy sets. In the dependent case, we demonstrate the robustness of OMD dynamics experimentally by simulating them in online Fisher markets, a canonical example of a min-max Stackelberg game with dependent strategy sets.

Convex-Concave Min-Max Stackelberg Games

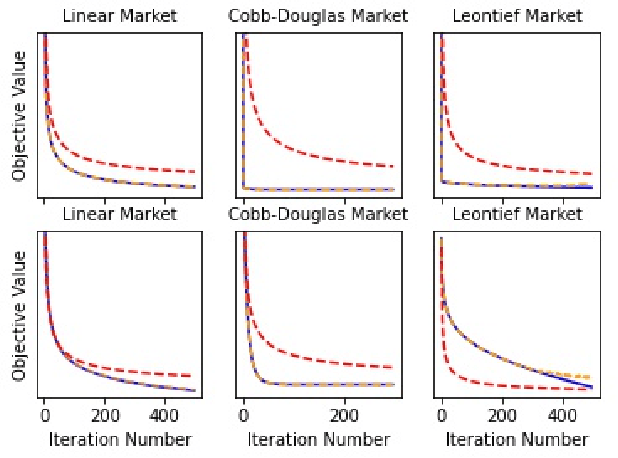
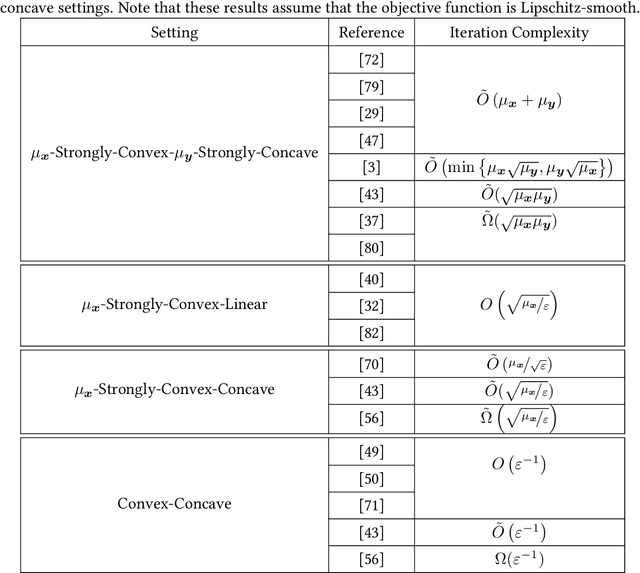
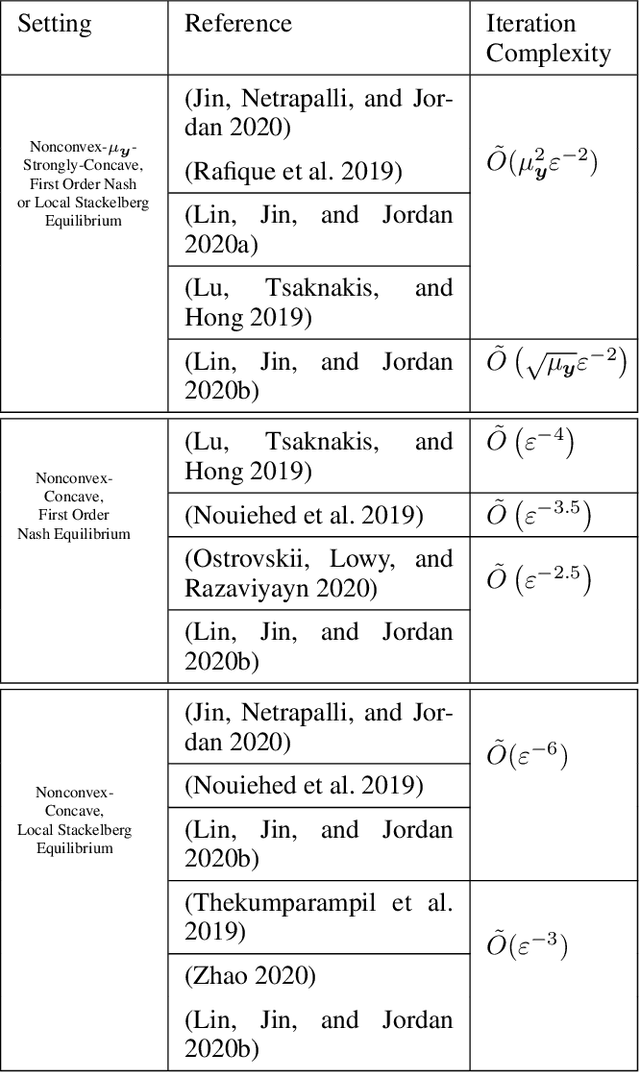
Min-max optimization problems (i.e., min-max games) have been attracting a great deal of attention because of their applicability to a wide range of machine learning problems. Although significant progress has been made recently, the literature to date has focused on games with independent strategy sets; little is known about solving games with dependent strategy sets, which can be characterized as min-max Stackelberg games. We introduce two first-order methods that solve a large class of convex-concave min-max Stackelberg games, and show that our methods converge in polynomial time. Min-max Stackelberg games were first studied by Wald, under the posthumous name of Wald's maximin model, a variant of which is the main paradigm used in robust optimization, which means that our methods can likewise solve many convex robust optimization problems. We observe that the computation of competitive equilibria in Fisher markets also comprises a min-max Stackelberg game. Further, we demonstrate the efficacy and efficiency of our algorithms in practice by computing competitive equilibria in Fisher markets with varying utility structures. Our experiments suggest potential ways to extend our theoretical results, by demonstrating how different smoothness properties can affect the convergence rate of our algorithms.