Robust No-Regret Learning in Min-Max Stackelberg Games
Paper and Code
Apr 13, 2022
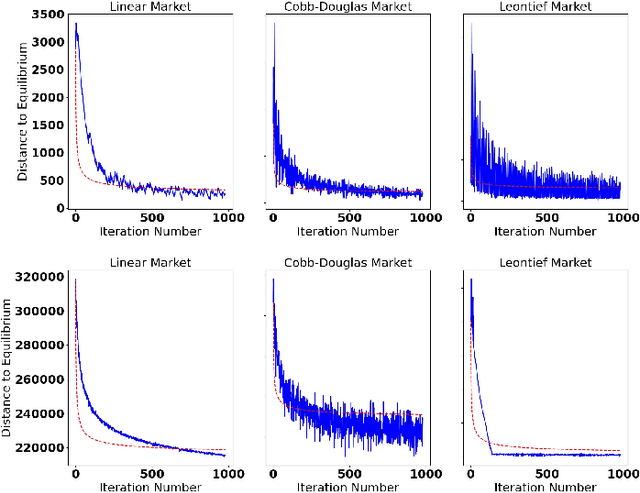
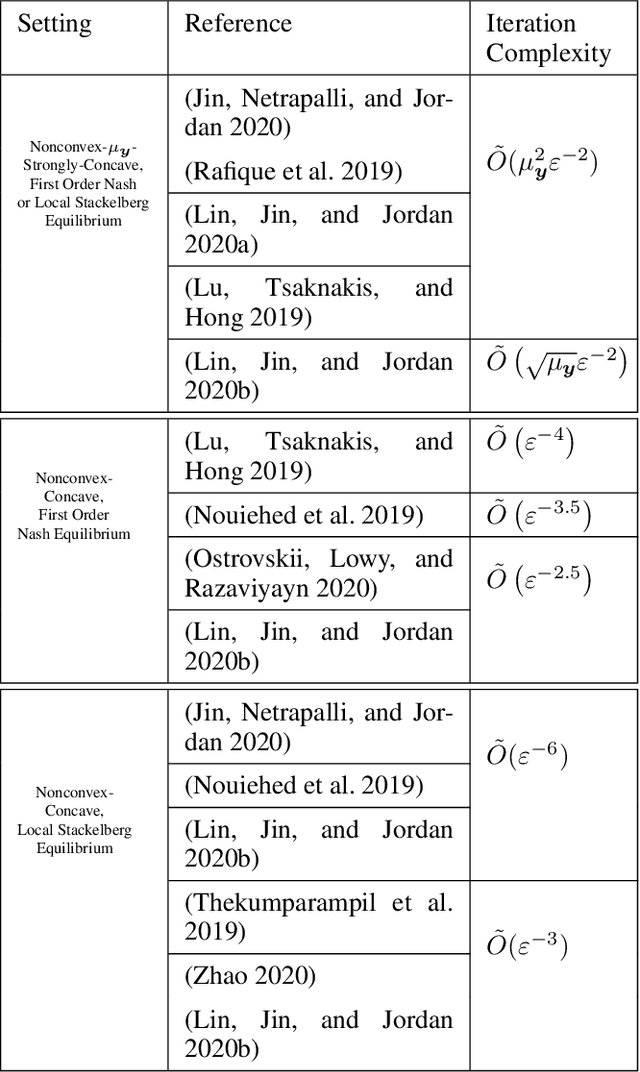
The behavior of no-regret learning algorithms is well understood in two-player min-max (i.e, zero-sum) games. In this paper, we investigate the behavior of no-regret learning in min-max games with dependent strategy sets, where the strategy of the first player constrains the behavior of the second. Such games are best understood as sequential, i.e., min-max Stackelberg, games. We consider two settings, one in which only the first player chooses their actions using a no-regret algorithm while the second player best responds, and one in which both players use no-regret algorithms. For the former case, we show that no-regret dynamics converge to a Stackelberg equilibrium. For the latter case, we introduce a new type of regret, which we call Lagrangian regret, and show that if both players minimize their Lagrangian regrets, then play converges to a Stackelberg equilibrium. We then observe that online mirror descent (OMD) dynamics in these two settings correspond respectively to a known nested (i.e., sequential) gradient descent-ascent (GDA) algorithm and a new simultaneous GDA-like algorithm, thereby establishing convergence of these algorithms to Stackelberg equilibrium. Finally, we analyze the robustness of OMD dynamics to perturbations by investigating online min-max Stackelberg games. We prove that OMD dynamics are robust for a large class of online min-max games with independent strategy sets. In the dependent case, we demonstrate the robustness of OMD dynamics experimentally by simulating them in online Fisher markets, a canonical example of a min-max Stackelberg game with dependent strategy sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge