Sequential Estimation under Multiple Resources: a Bandit Point of View
Paper and Code
Sep 29, 2021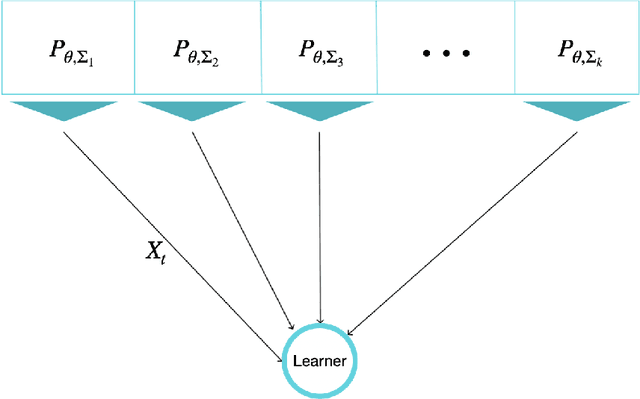
The problem of Sequential Estimation under Multiple Resources (SEMR) is defined in a federated setting. SEMR could be considered as the intersection of statistical estimation and bandit theory. In this problem, an agent is confronting with k resources to estimate a parameter $\theta$. The agent should continuously learn the quality of the resources by wisely choosing them and at the end, proposes an estimator based on the collected data. In this paper, we assume that the resources' distributions are Gaussian. The quality of the final estimator is evaluated by its mean squared error. Also, we restrict our class of estimators to unbiased estimators in order to define a meaningful notion of regret. The regret measures the performance of the agent by the variance of the final estimator in comparison to the optimal variance. We propose a lower bound to determine the fundamental limit of the setting even in the case that the distributions are not Gaussian. Also, we offer an order-optimal algorithm to achieve this lower bound.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge