Fundamental limits of distributed covariance matrix estimation via a conditional strong data processing inequality

Estimating high-dimensional covariance matrices is a key task across many fields. This paper explores the theoretical limits of distributed covariance estimation in a feature-split setting, where communication between agents is constrained. Specifically, we study a scenario in which multiple agents each observe different components of i.i.d. samples drawn from a sub-Gaussian random vector. A central server seeks to estimate the complete covariance matrix using a limited number of bits communicated by each agent. We obtain a nearly tight minimax lower bound for covariance matrix estimation under operator norm and Frobenius norm. Our main technical tool is a novel generalization of the strong data processing inequality (SDPI), termed the Conditional Strong Data Processing Inequality (C-SDPI) coefficient, introduced in this work. The C-SDPI coefficient shares key properties such as tensorization with the conventional SDPI. Crucially, it quantifies the average contraction in a state-dependent channel and can be significantly lower than the worst-case SDPI coefficient over the state input. Utilizing the doubling trick of Geng-Nair and an operator Jensen inequality, we compute this coefficient for Gaussian mixture channels. We then employ it to establish minimax lower bounds on estimation error, capturing the trade-offs among sample size, communication cost, and data dimensionality. Building on this, we present a nearly optimal estimation protocol whose sample and communication requirements match the lower bounds up to logarithmic factors. Unlike much of the existing literature, our framework does not assume infinite samples or Gaussian distributions, making it broadly applicable. Finally, we extend our analysis to interactive protocols, showing interaction can significantly reduce communication requirements compared to non-interactive schemes.

A New Approach to Backtracking Counterfactual Explanations: A Causal Framework for Efficient Model Interpretability

Counterfactual explanations enhance interpretability by identifying alternative inputs that produce different outputs, offering localized insights into model decisions. However, traditional methods often neglect causal relationships, leading to unrealistic examples. While newer approaches integrate causality, they are computationally expensive. To address these challenges, we propose an efficient method based on backtracking counterfactuals that incorporates causal reasoning to generate actionable explanations. We first examine the limitations of existing methods and then introduce our novel approach and its features. We also explore the relationship between our method and previous techniques, demonstrating that it generalizes them in specific scenarios. Finally, experiments show that our method provides deeper insights into model outputs.

Supermodular f-divergences and bounds on lossy compression and generalization error with mutual f-information

In this paper, we introduce super-modular $\mf$-divergences and provide three applications for them: (i) we introduce Sanov's upper bound on the tail probability of sum of independent random variables based on super-modular $\mf$-divergence and show that our generalized Sanov's bound strictly improves over ordinary one, (ii) we consider the lossy compression problem which studies the set of achievable rates for a given distortion and code length. We extend the rate-distortion function using mutual $\mf$-information and provide new and strictly better bounds on achievable rates in the finite blocklength regime using super-modular $\mf$-divergences, and (iii) we provide a connection between the generalization error of algorithms with bounded input/output mutual $\mf$-information and a generalized rate-distortion problem. This connection allows us to bound the generalization error of learning algorithms using lower bounds on the rate-distortion function. Our bound is based on a new lower bound on the rate-distortion function that (for some examples) strictly improves over previously best-known bounds. Moreover, super-modular $\mf$-divergences are utilized to reduce the dimension of the problem and obtain single-letter bounds.

Sequential Estimation under Multiple Resources: a Bandit Point of View

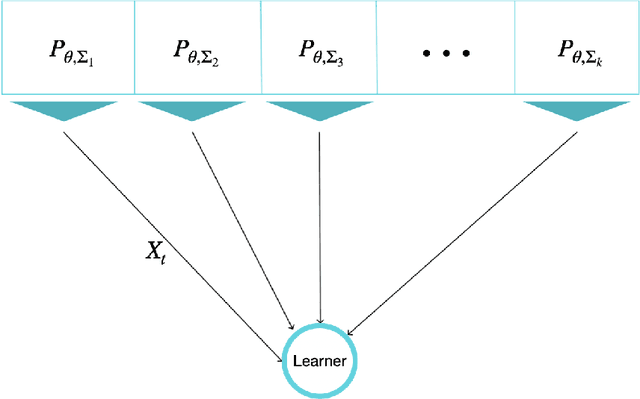
The problem of Sequential Estimation under Multiple Resources (SEMR) is defined in a federated setting. SEMR could be considered as the intersection of statistical estimation and bandit theory. In this problem, an agent is confronting with k resources to estimate a parameter $\theta$. The agent should continuously learn the quality of the resources by wisely choosing them and at the end, proposes an estimator based on the collected data. In this paper, we assume that the resources' distributions are Gaussian. The quality of the final estimator is evaluated by its mean squared error. Also, we restrict our class of estimators to unbiased estimators in order to define a meaningful notion of regret. The regret measures the performance of the agent by the variance of the final estimator in comparison to the optimal variance. We propose a lower bound to determine the fundamental limit of the setting even in the case that the distributions are not Gaussian. Also, we offer an order-optimal algorithm to achieve this lower bound.