Exact Gap between Generalization Error and Uniform Convergence in Random Feature Models
Paper and Code
Mar 08, 2021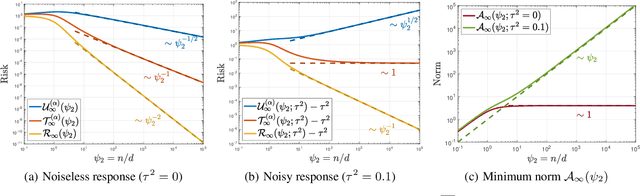
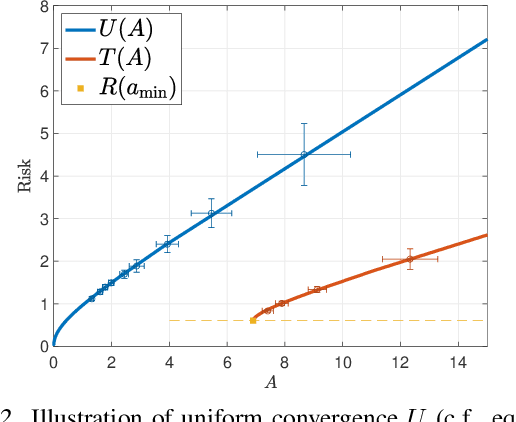
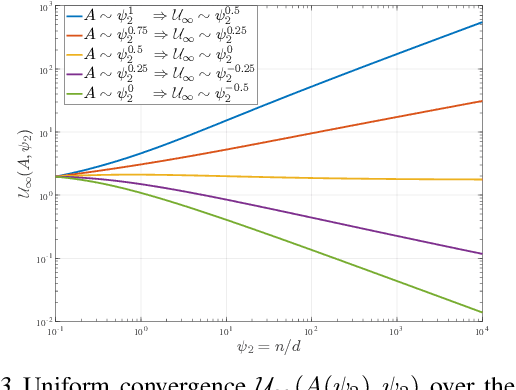
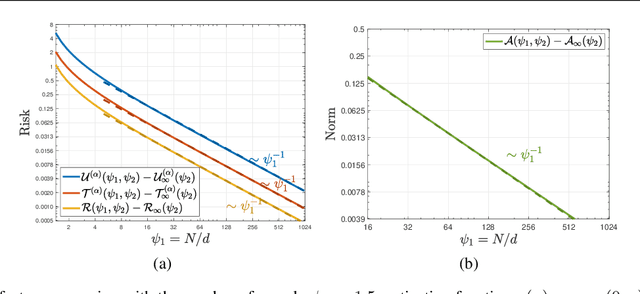
Recent work showed that there could be a large gap between the classical uniform convergence bound and the actual test error of zero-training-error predictors (interpolators) such as deep neural networks. To better understand this gap, we study the uniform convergence in the nonlinear random feature model and perform a precise theoretical analysis on how uniform convergence depends on the sample size and the number of parameters. We derive and prove analytical expressions for three quantities in this model: 1) classical uniform convergence over norm balls, 2) uniform convergence over interpolators in the norm ball (recently proposed by Zhou et al. (2020)), and 3) the risk of minimum norm interpolator. We show that, in the setting where the classical uniform convergence bound is vacuous (diverges to $\infty$), uniform convergence over the interpolators still gives a non-trivial bound of the test error of interpolating solutions. We also showcase a different setting where classical uniform convergence bound is non-vacuous, but uniform convergence over interpolators can give an improved sample complexity guarantee. Our result provides a first exact comparison between the test errors and uniform convergence bounds for interpolators beyond simple linear models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge