Music Arena: Live Evaluation for Text-to-Music

We present Music Arena, an open platform for scalable human preference evaluation of text-to-music (TTM) models. Soliciting human preferences via listening studies is the gold standard for evaluation in TTM, but these studies are expensive to conduct and difficult to compare, as study protocols may differ across systems. Moreover, human preferences might help researchers align their TTM systems or improve automatic evaluation metrics, but an open and renewable source of preferences does not currently exist. We aim to fill these gaps by offering *live* evaluation for TTM. In Music Arena, real-world users input text prompts of their choosing and compare outputs from two TTM systems, and their preferences are used to compile a leaderboard. While Music Arena follows recent evaluation trends in other AI domains, we also design it with key features tailored to music: an LLM-based routing system to navigate the heterogeneous type signatures of TTM systems, and the collection of *detailed* preferences including listening data and natural language feedback. We also propose a rolling data release policy with user privacy guarantees, providing a renewable source of preference data and increasing platform transparency. Through its standardized evaluation protocol, transparent data access policies, and music-specific features, Music Arena not only addresses key challenges in the TTM ecosystem but also demonstrates how live evaluation can be thoughtfully adapted to unique characteristics of specific AI domains. Music Arena is available at: https://music-arena.org

Cost-Optimal Active AI Model Evaluation

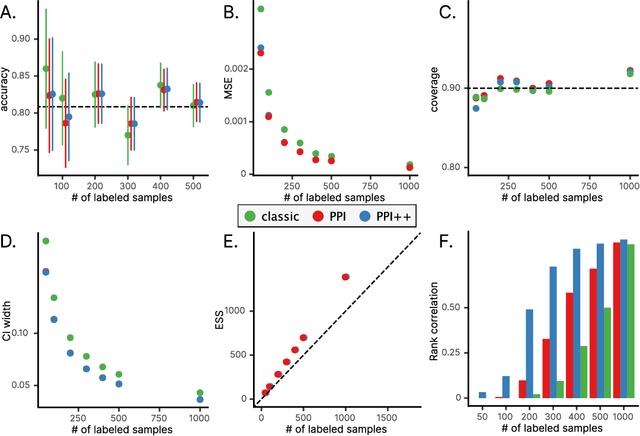
The development lifecycle of generative AI systems requires continual evaluation, data acquisition, and annotation, which is costly in both resources and time. In practice, rapid iteration often makes it necessary to rely on synthetic annotation data because of the low cost, despite the potential for substantial bias. In this paper, we develop novel, cost-aware methods for actively balancing the use of a cheap, but often inaccurate, weak rater -- such as a model-based autorater that is designed to automatically assess the quality of generated content -- with a more expensive, but also more accurate, strong rater alternative such as a human. More specifically, the goal of our approach is to produce a low variance, unbiased estimate of the mean of the target "strong" rating, subject to some total annotation budget. Building on recent work in active and prediction-powered statistical inference, we derive a family of cost-optimal policies for allocating a given annotation budget between weak and strong raters so as to maximize statistical efficiency. Using synthetic and real-world data, we empirically characterize the conditions under which these policies yield improvements over prior methods. We find that, especially in tasks where there is high variability in the difficulty of examples, our policies can achieve the same estimation precision at a far lower total annotation budget than standard evaluation methods.

Search Arena: Analyzing Search-Augmented LLMs

Search-augmented language models combine web search with Large Language Models (LLMs) to improve response groundedness and freshness. However, analyzing these systems remains challenging: existing datasets are limited in scale and narrow in scope, often constrained to static, single-turn, fact-checking questions. In this work, we introduce Search Arena, a crowd-sourced, large-scale, human-preference dataset of over 24,000 paired multi-turn user interactions with search-augmented LLMs. The dataset spans diverse intents and languages, and contains full system traces with around 12,000 human preference votes. Our analysis reveals that user preferences are influenced by the number of citations, even when the cited content does not directly support the attributed claims, uncovering a gap between perceived and actual credibility. Furthermore, user preferences vary across cited sources, revealing that community-driven platforms are generally preferred and static encyclopedic sources are not always appropriate and reliable. To assess performance across different settings, we conduct cross-arena analyses by testing search-augmented LLMs in a general-purpose chat environment and conventional LLMs in search-intensive settings. We find that web search does not degrade and may even improve performance in non-search settings; however, the quality in search settings is significantly affected if solely relying on the model's parametric knowledge. We open-sourced the dataset to support future research in this direction. Our dataset and code are available at: https://github.com/lmarena/search-arena.

Prompt-to-Leaderboard

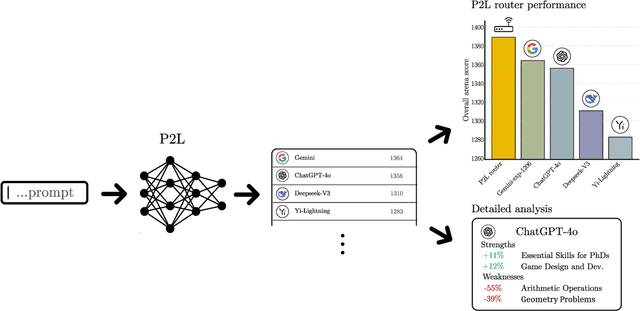
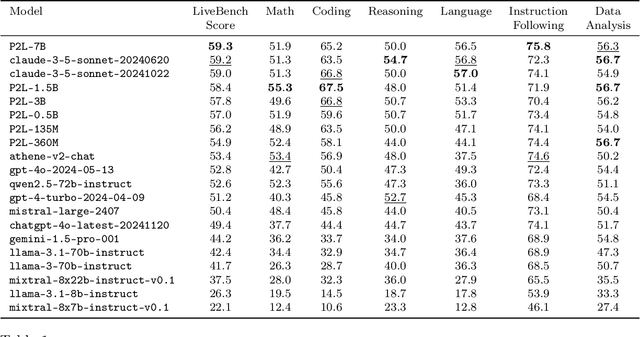
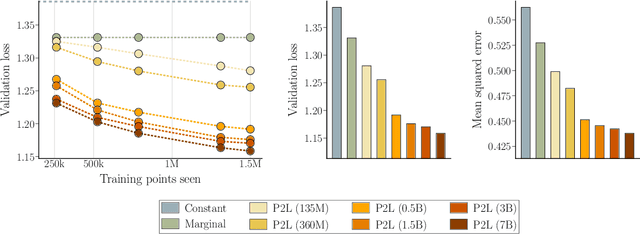
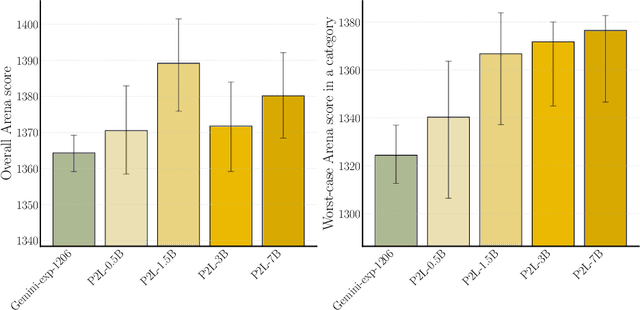
Large language model (LLM) evaluations typically rely on aggregated metrics like accuracy or human preference, averaging across users and prompts. This averaging obscures user- and prompt-specific variations in model performance. To address this, we propose Prompt-to-Leaderboard (P2L), a method that produces leaderboards specific to a prompt. The core idea is to train an LLM taking natural language prompts as input to output a vector of Bradley-Terry coefficients which are then used to predict the human preference vote. The resulting prompt-dependent leaderboards allow for unsupervised task-specific evaluation, optimal routing of queries to models, personalization, and automated evaluation of model strengths and weaknesses. Data from Chatbot Arena suggest that P2L better captures the nuanced landscape of language model performance than the averaged leaderboard. Furthermore, our findings suggest that P2L's ability to produce prompt-specific evaluations follows a power law scaling similar to that observed in LLMs themselves. In January 2025, the router we trained based on this methodology achieved the \#1 spot in the Chatbot Arena leaderboard. Our code is available at this GitHub link: https://github.com/lmarena/p2l.

Gradient Equilibrium in Online Learning: Theory and Applications

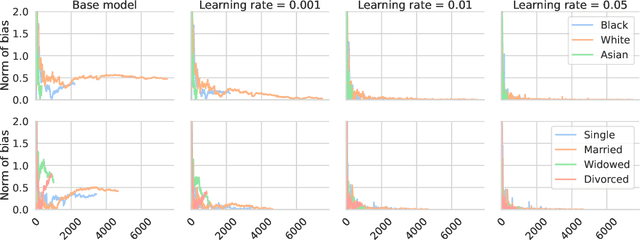
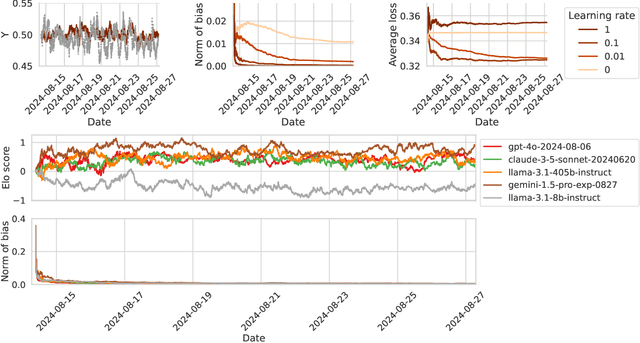
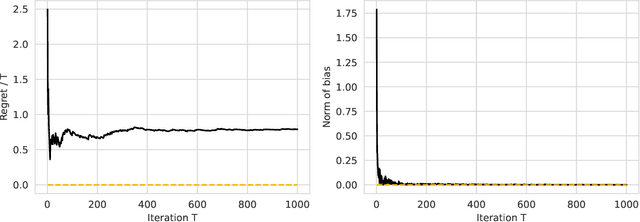
We present a new perspective on online learning that we refer to as gradient equilibrium: a sequence of iterates achieves gradient equilibrium if the average of gradients of losses along the sequence converges to zero. In general, this condition is not implied by nor implies sublinear regret. It turns out that gradient equilibrium is achievable by standard online learning methods such as gradient descent and mirror descent with constant step sizes (rather than decaying step sizes, as is usually required for no regret). Further, as we show through examples, gradient equilibrium translates into an interpretable and meaningful property in online prediction problems spanning regression, classification, quantile estimation, and others. Notably, we show that the gradient equilibrium framework can be used to develop a debiasing scheme for black-box predictions under arbitrary distribution shift, based on simple post hoc online descent updates. We also show that post hoc gradient updates can be used to calibrate predicted quantiles under distribution shift, and that the framework leads to unbiased Elo scores for pairwise preference prediction.

Theoretical Foundations of Conformal Prediction

This book is about conformal prediction and related inferential techniques that build on permutation tests and exchangeability. These techniques are useful in a diverse array of tasks, including hypothesis testing and providing uncertainty quantification guarantees for machine learning systems. Much of the current interest in conformal prediction is due to its ability to integrate into complex machine learning workflows, solving the problem of forming prediction sets without any assumptions on the form of the data generating distribution. Since contemporary machine learning algorithms have generally proven difficult to analyze directly, conformal prediction's main appeal is its ability to provide formal, finite-sample guarantees when paired with such methods. The goal of this book is to teach the reader about the fundamental technical arguments that arise when researching conformal prediction and related questions in distribution-free inference. Many of these proof strategies, especially the more recent ones, are scattered among research papers, making it difficult for researchers to understand where to look, which results are important, and how exactly the proofs work. We hope to bridge this gap by curating what we believe to be some of the most important results in the literature and presenting their proofs in a unified language, with illustrations, and with an eye towards pedagogy.

How to Evaluate Reward Models for RLHF

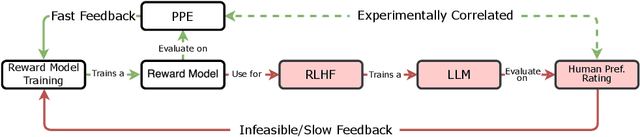
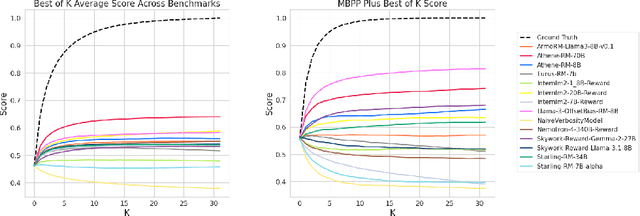
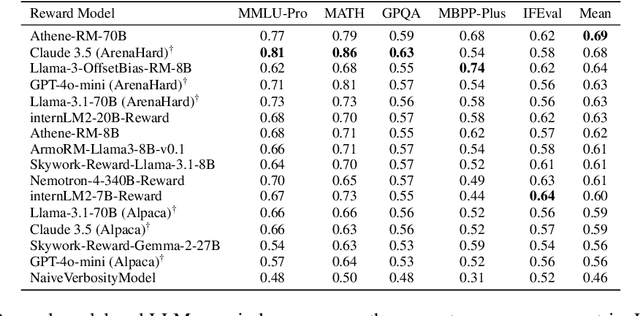
We introduce a new benchmark for reward models that quantifies their ability to produce strong language models through RLHF (Reinforcement Learning from Human Feedback). The gold-standard approach is to run a full RLHF training pipeline and directly probe downstream LLM performance. However, this process is prohibitively expensive. To address this, we build a predictive model of downstream LLM performance by evaluating the reward model on proxy tasks. These proxy tasks consist of a large-scale human preference and a verifiable correctness preference dataset, in which we measure 12 metrics across 12 domains. To investigate which reward model metrics are most correlated to gold-standard RLHF outcomes, we launch an end-to-end RLHF experiment on a large-scale crowdsourced human preference platform to view real reward model downstream performance as ground truth. Ultimately, we compile our data and findings into Preference Proxy Evaluations (PPE), the first reward model benchmark explicitly linked to post-RLHF real-world human preference performance, which we open-source for public use and further development. Our code and evaluations can be found at https://github.com/lmarena/PPE .

Data-Adaptive Tradeoffs among Multiple Risks in Distribution-Free Prediction

Decision-making pipelines are generally characterized by tradeoffs among various risk functions. It is often desirable to manage such tradeoffs in a data-adaptive manner. As we demonstrate, if this is done naively, state-of-the art uncertainty quantification methods can lead to significant violations of putative risk guarantees. To address this issue, we develop methods that permit valid control of risk when threshold and tradeoff parameters are chosen adaptively. Our methodology supports monotone and nearly-monotone risks, but otherwise makes no distributional assumptions. To illustrate the benefits of our approach, we carry out numerical experiments on synthetic data and the large-scale vision dataset MS-COCO.

AutoEval Done Right: Using Synthetic Data for Model Evaluation

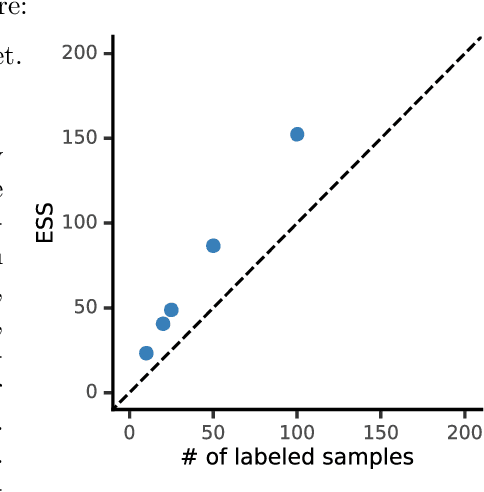
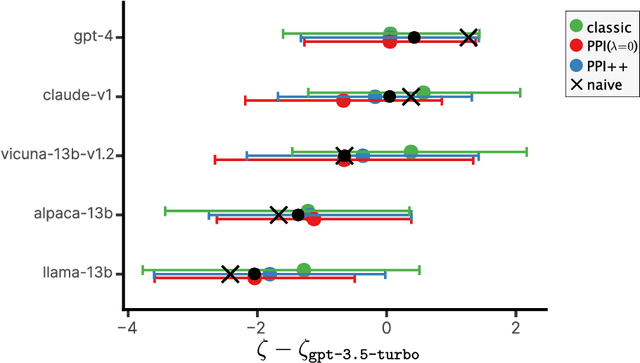
The evaluation of machine learning models using human-labeled validation data can be expensive and time-consuming. AI-labeled synthetic data can be used to decrease the number of human annotations required for this purpose in a process called autoevaluation. We suggest efficient and statistically principled algorithms for this purpose that improve sample efficiency while remaining unbiased. These algorithms increase the effective human-labeled sample size by up to 50% on experiments with GPT-4.

Wavefront Randomization Improves Deconvolution

The performance of an imaging system is limited by optical aberrations, which cause blurriness in the resulting image. Digital correction techniques, such as deconvolution, have limited ability to correct the blur, since some spatial frequencies in the scene are not measured adequately (i.e., 'zeros' of the system transfer function). We prove that the addition of a random mask to an imaging system removes its dependence on aberrations, reducing the likelihood of zeros in the transfer function and consequently decreasing the sensitivity to noise during deconvolution. In simulation, we show that this strategy improves image quality over a range of aberration types, aberration strengths, and signal-to-noise ratios.