Data-Adaptive Tradeoffs among Multiple Risks in Distribution-Free Prediction

Decision-making pipelines are generally characterized by tradeoffs among various risk functions. It is often desirable to manage such tradeoffs in a data-adaptive manner. As we demonstrate, if this is done naively, state-of-the art uncertainty quantification methods can lead to significant violations of putative risk guarantees. To address this issue, we develop methods that permit valid control of risk when threshold and tradeoff parameters are chosen adaptively. Our methodology supports monotone and nearly-monotone risks, but otherwise makes no distributional assumptions. To illustrate the benefits of our approach, we carry out numerical experiments on synthetic data and the large-scale vision dataset MS-COCO.

On the design-dependent suboptimality of the Lasso

This paper investigates the effect of the design matrix on the ability (or inability) to estimate a sparse parameter in linear regression. More specifically, we characterize the optimal rate of estimation when the smallest singular value of the design matrix is bounded away from zero. In addition to this information-theoretic result, we provide and analyze a procedure which is simultaneously statistically optimal and computationally efficient, based on soft thresholding the ordinary least squares estimator. Most surprisingly, we show that the Lasso estimator -- despite its widespread adoption for sparse linear regression -- is provably minimax rate-suboptimal when the minimum singular value is small. We present a family of design matrices and sparse parameters for which we can guarantee that the Lasso with any choice of regularization parameter -- including those which are data-dependent and randomized -- would fail in the sense that its estimation rate is suboptimal by polynomial factors in the sample size. Our lower bound is strong enough to preclude the statistical optimality of all forms of the Lasso, including its highly popular penalized, norm-constrained, and cross-validated variants.

Transformers can optimally learn regression mixture models

Mixture models arise in many regression problems, but most methods have seen limited adoption partly due to these algorithms' highly-tailored and model-specific nature. On the other hand, transformers are flexible, neural sequence models that present the intriguing possibility of providing general-purpose prediction methods, even in this mixture setting. In this work, we investigate the hypothesis that transformers can learn an optimal predictor for mixtures of regressions. We construct a generative process for a mixture of linear regressions for which the decision-theoretic optimal procedure is given by data-driven exponential weights on a finite set of parameters. We observe that transformers achieve low mean-squared error on data generated via this process. By probing the transformer's output at inference time, we also show that transformers typically make predictions that are close to the optimal predictor. Our experiments also demonstrate that transformers can learn mixtures of regressions in a sample-efficient fashion and are somewhat robust to distribution shifts. We complement our experimental observations by proving constructively that the decision-theoretic optimal procedure is indeed implementable by a transformer.

Optimally tackling covariate shift in RKHS-based nonparametric regression

We study the covariate shift problem in the context of nonparametric regression over a reproducing kernel Hilbert space (RKHS). We focus on two natural families of covariate shift problems defined using the likelihood ratios between the source and target distributions. When the likelihood ratios are uniformly bounded, we prove that the kernel ridge regression (KRR) estimator with a carefully chosen regularization parameter is minimax rate-optimal (up to a log factor) for a large family of RKHSs with regular kernel eigenvalues. Interestingly, KRR does not require full knowledge of the likelihood ratio apart from an upper bound on it. In striking contrast to the standard statistical setting without covariate shift, we also demonstrate that a na\"\i ve estimator, which minimizes the empirical risk over the function class, is strictly suboptimal under covariate shift as compared to KRR. We then address the larger class of covariate shift problems where likelihood ratio is possibly unbounded yet has a finite second moment. Here, we show via careful simulations that KRR fails to attain the optimal rate. Instead, we propose a reweighted KRR estimator that weights samples based on a careful truncation of the likelihood ratios. Again, we are able to show that this estimator is minimax optimal, up to logarithmic factors.

A new similarity measure for covariate shift with applications to nonparametric regression

We study covariate shift in the context of nonparametric regression. We introduce a new measure of distribution mismatch between the source and target distributions that is based on the integrated ratio of probabilities of balls at a given radius. We use the scaling of this measure with respect to the radius to characterize the minimax rate of estimation over a family of H\"older continuous functions under covariate shift. In comparison to the recently proposed notion of transfer exponent, this measure leads to a sharper rate of convergence and is more fine-grained. We accompany our theory with concrete instances of covariate shift that illustrate this sharp difference.

Cluster-and-Conquer: A Framework For Time-Series Forecasting

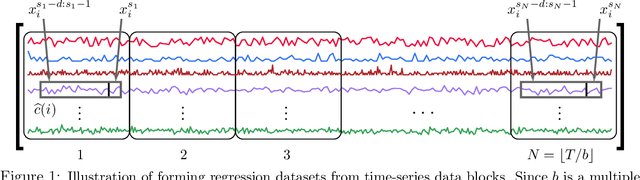
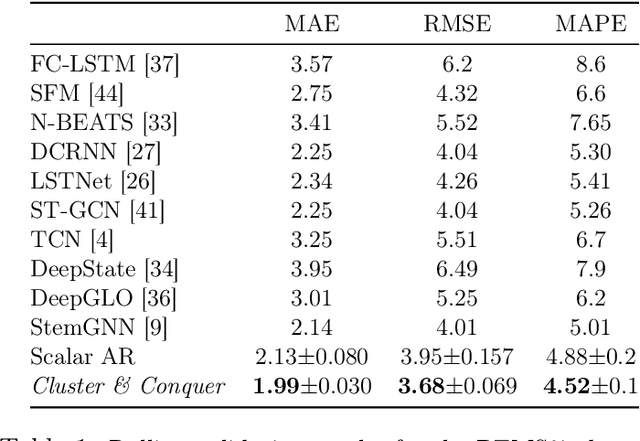
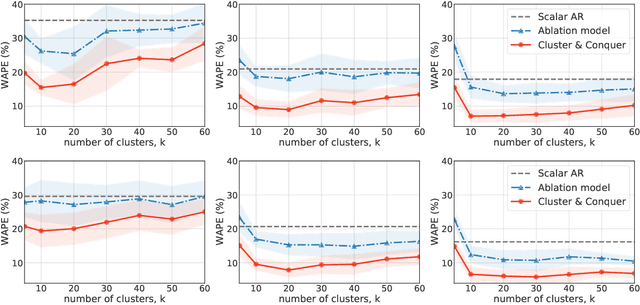
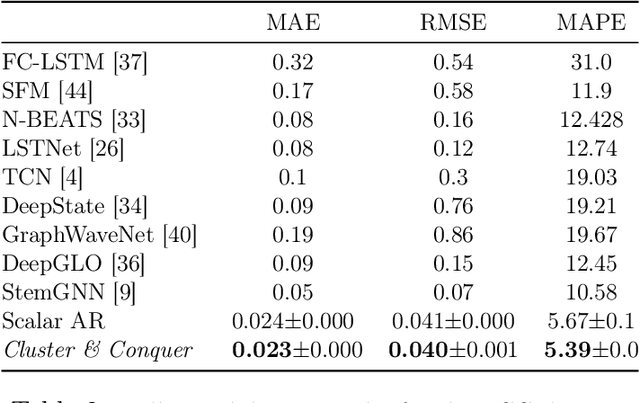
We propose a three-stage framework for forecasting high-dimensional time-series data. Our method first estimates parameters for each univariate time series. Next, we use these parameters to cluster the time series. These clusters can be viewed as multivariate time series, for which we then compute parameters. The forecasted values of a single time series can depend on the history of other time series in the same cluster, accounting for intra-cluster similarity while minimizing potential noise in predictions by ignoring inter-cluster effects. Our framework -- which we refer to as "cluster-and-conquer" -- is highly general, allowing for any time-series forecasting and clustering method to be used in each step. It is computationally efficient and embarrassingly parallel. We motivate our framework with a theoretical analysis in an idealized mixed linear regression setting, where we provide guarantees on the quality of the estimates. We accompany these guarantees with experimental results that demonstrate the advantages of our framework: when instantiated with simple linear autoregressive models, we are able to achieve state-of-the-art results on several benchmark datasets, sometimes outperforming deep-learning-based approaches.

FedSplit: An algorithmic framework for fast federated optimization

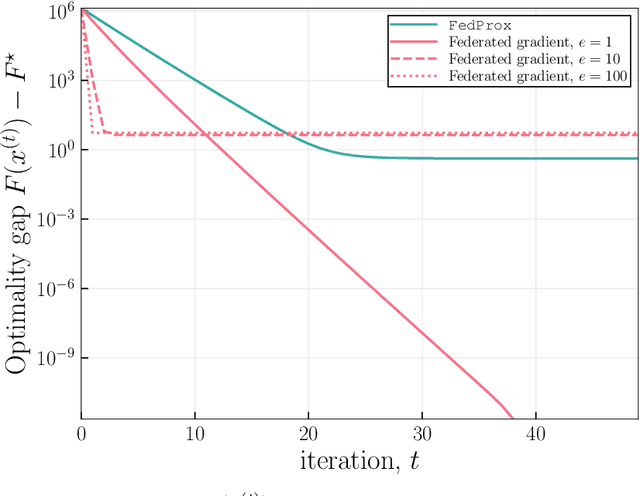
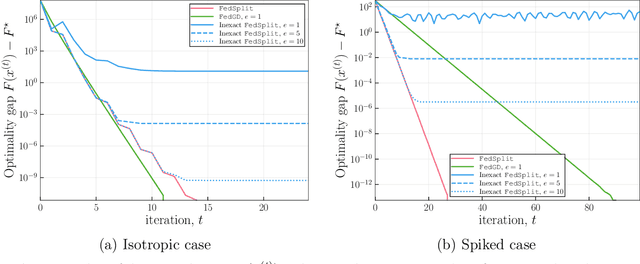
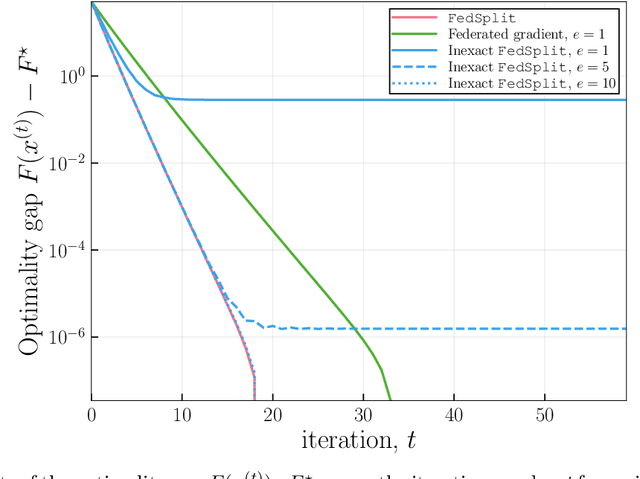
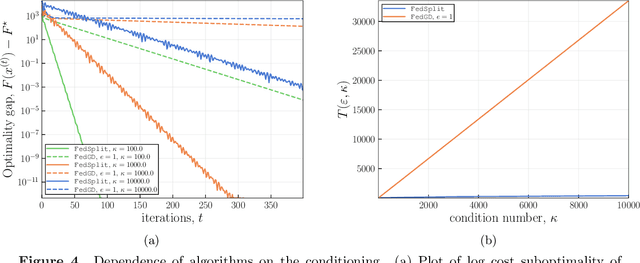
Motivated by federated learning, we consider the hub-and-spoke model of distributed optimization in which a central authority coordinates the computation of a solution among many agents while limiting communication. We first study some past procedures for federated optimization, and show that their fixed points need not correspond to stationary points of the original optimization problem, even in simple convex settings with deterministic updates. In order to remedy these issues, we introduce FedSplit, a class of algorithms based on operator splitting procedures for solving distributed convex minimization with additive structure. We prove that these procedures have the correct fixed points, corresponding to optima of the original optimization problem, and we characterize their convergence rates under different settings. Our theory shows that these methods are provably robust to inexact computation of intermediate local quantities. We complement our theory with some simple experiments that demonstrate the benefits of our methods in practice.