Ariane Marandon
Selecting informative conformal prediction sets with false coverage rate control
Mar 18, 2024Abstract:In supervised learning, including regression and classification, conformal methods provide prediction sets for the outcome/label with finite sample coverage for any machine learning predictors. We consider here the case where such prediction sets come after a selection process. The selection process requires that the selected prediction sets be `informative' in a well defined sense. We consider both the classification and regression settings where the analyst may consider as informative only the sample with prediction label sets or prediction intervals small enough, excluding null values, or obeying other appropriate `monotone' constraints. While this covers many settings of possible interest in various applications, we develop a unified framework for building such informative conformal prediction sets while controlling the false coverage rate (FCR) on the selected sample. While conformal prediction sets after selection have been the focus of much recent literature in the field, the new introduced procedures, called InfoSP and InfoSCOP, are to our knowledge the first ones providing FCR control for informative prediction sets. We show the usefulness of our resulting procedures on real and simulated data.
Conformal link prediction to control the error rate
Jun 26, 2023Abstract:Most link prediction methods return estimates of the connection probability of missing edges in a graph. Such output can be used to rank the missing edges, from most to least likely to be a true edge, but it does not directly provide a classification into true and non-existent. In this work, we consider the problem of identifying a set of true edges with a control of the false discovery rate (FDR). We propose a novel method based on high-level ideas from the literature on conformal inference. The graph structure induces intricate dependence in the data, which we carefully take into account, as this makes the setup different from the usual setup in conformal inference, where exchangeability is assumed. The FDR control is empirically demonstrated for both simulated and real data.
Machine learning meets false discovery rate
Aug 13, 2022
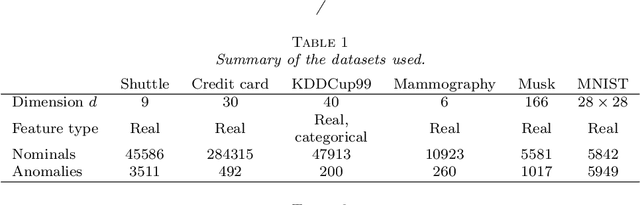
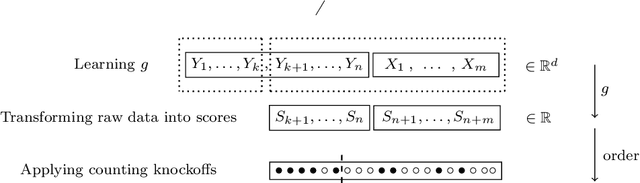

Abstract:Classical false discovery rate (FDR) controlling procedures offer strong and interpretable guarantees, while they often lack of flexibility. On the other hand, recent machine learning classification algorithms, as those based on random forests (RF) or neural networks (NN), have great practical performances but lack of interpretation and of theoretical guarantees. In this paper, we make these two meet by introducing a new adaptive novelty detection procedure with FDR control, called AdaDetect. It extends the scope of recent works of multiple testing literature to the high dimensional setting, notably the one in Yang et al. (2021). AdaDetect is shown to both control strongly the FDR and to have a power that mimics the one of the oracle in a specific sense. The interest and validity of our approach is demonstrated with theoretical results, numerical experiments on several benchmark datasets and with an application to astrophysical data. In particular, while AdaDetect can be used in combination with any classifier, it is particularly efficient on real-world datasets with RF, and on images with NN.
False clustering rate control in mixture models
Mar 08, 2022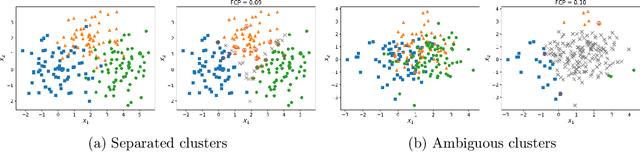
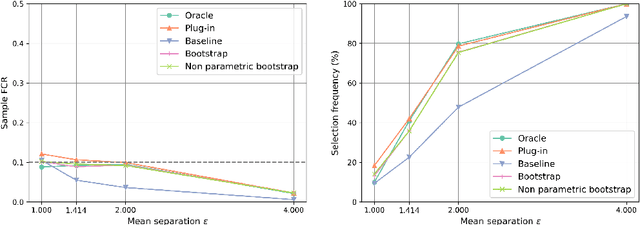
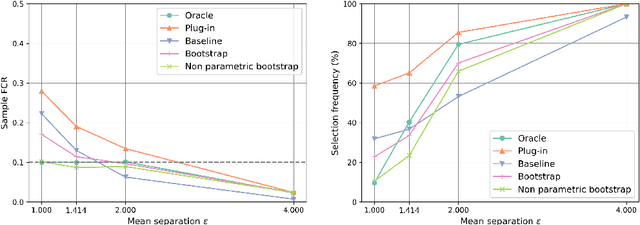
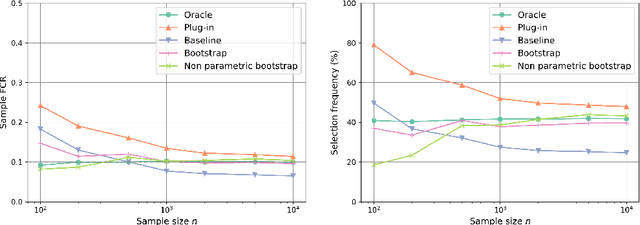
Abstract:The clustering task consists in delivering labels to the members of a sample. For most data sets, some individuals are ambiguous and intrinsically difficult to attribute to one or another cluster. However, in practical applications, misclassifying individuals is potentially disastrous. To overcome this difficulty, the idea followed here is to classify only a part of the sample in order to obtain a small misclassification rate. This approach is well known in the supervised setting, and referred to as classification with an abstention option. The purpose of this paper is to revisit this approach in an unsupervised mixture-model framework. The problem is formalized in terms of controlling the false clustering rate (FCR) below a prescribed level {\alpha}, while maximizing the number of classified items. New procedures are introduced and their behavior is shown to be close to the optimal one by establishing theoretical results and conducting numerical experiments. An application to breast cancer data illustrates the benefits of the new approach from a practical viewpoint.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge