Data-Driven Score-Based Models for Generating Stable Structures with Adaptive Crystal Cells

The discovery of new functional and stable materials is a big challenge due to its complexity. This work aims at the generation of new crystal structures with desired properties, such as chemical stability and specified chemical composition, by using machine learning generative models. Compared to the generation of molecules, crystal structures pose new difficulties arising from the periodic nature of the crystal and from the specific symmetry constraints related to the space group. In this work, score-based probabilistic models based on annealed Langevin dynamics, which have shown excellent performance in various applications, are adapted to the task of crystal generation. The novelty of the presented approach resides in the fact that the lattice of the crystal cell is not fixed. During the training of the model, the lattice is learned from the available data, whereas during the sampling of a new chemical structure, two denoising processes are used in parallel to generate the lattice along the generation of the atomic positions. A multigraph crystal representation is introduced that respects symmetry constraints, yielding computational advantages and a better quality of the sampled structures. We show that our model is capable of generating new candidate structures in any chosen chemical system and crystal group without any additional training. To illustrate the functionality of the proposed method, a comparison of our model to other recent generative models, based on descriptor-based metrics, is provided.

False clustering rate control in mixture models

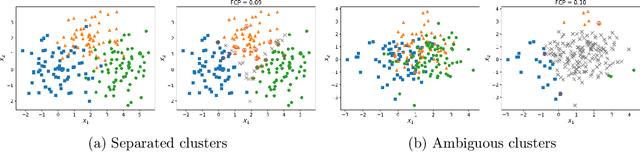
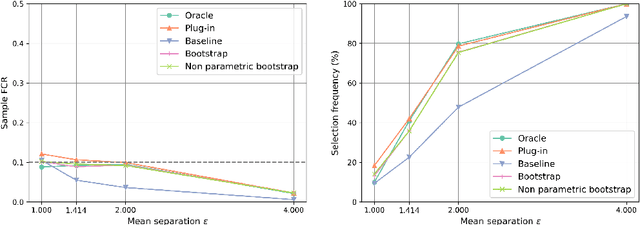
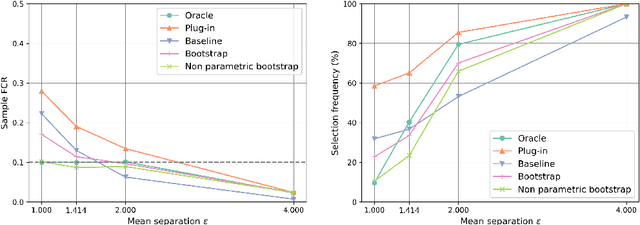
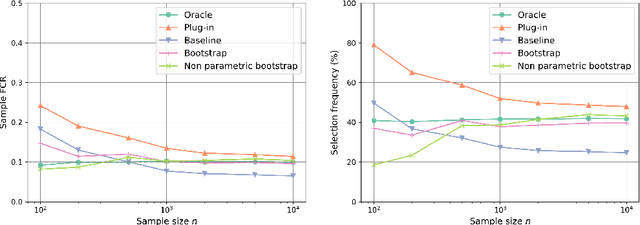
The clustering task consists in delivering labels to the members of a sample. For most data sets, some individuals are ambiguous and intrinsically difficult to attribute to one or another cluster. However, in practical applications, misclassifying individuals is potentially disastrous. To overcome this difficulty, the idea followed here is to classify only a part of the sample in order to obtain a small misclassification rate. This approach is well known in the supervised setting, and referred to as classification with an abstention option. The purpose of this paper is to revisit this approach in an unsupervised mixture-model framework. The problem is formalized in terms of controlling the false clustering rate (FCR) below a prescribed level {\alpha}, while maximizing the number of classified items. New procedures are introduced and their behavior is shown to be close to the optimal one by establishing theoretical results and conducting numerical experiments. An application to breast cancer data illustrates the benefits of the new approach from a practical viewpoint.

Properties of the Stochastic Approximation EM Algorithm with Mini-batch Sampling

To speed up convergence a mini-batch version of the Monte Carlo Markov Chain Stochastic Approximation Expectation Maximization (MCMC-SAEM) algorithm for general latent variable models is proposed. For exponential models the algorithm is shown to be convergent under classical conditions as the number of iterations increases. Numerical experiments illustrate the performance of the mini-batch algorithm in various models. In particular, we highlight that an appropriate choice of the mini-batch size results in a tremendous speed-up of the convergence of the sequence of estimators generated by the algorithm. Moreover, insights on the effect of the mini-batch size on the limit distribution are presented.