Dynamic Batch Learning in High-Dimensional Sparse Linear Contextual Bandits
Paper and Code
Aug 28, 2020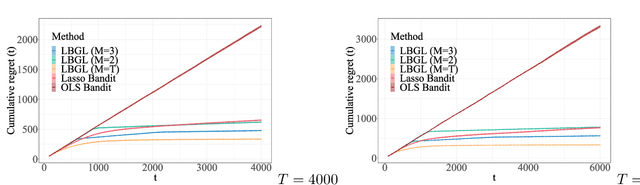
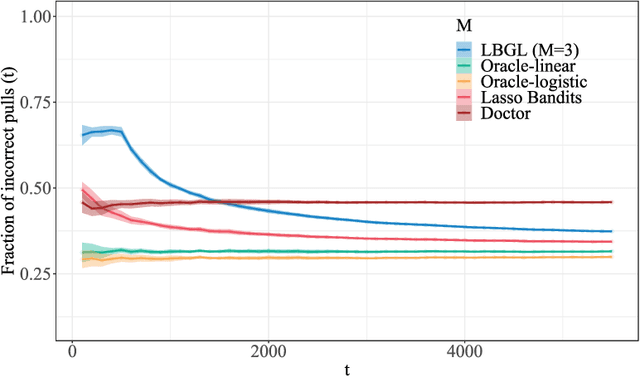
We study the problem of dynamic batch learning in high-dimensional sparse linear contextual bandits, where a decision maker, under a given maximum-number-of-batch constraint and only able to observe rewards at the end of each batch, can dynamically decide how many individuals to include in the next batch (at the end of the current batch) and what personalized action-selection scheme to adopt within each batch. Such batch constraints are ubiquitous in a variety of practical contexts, including personalized product offerings in marketing and medical treatment selection in clinical trials. We characterize the fundamental learning limit in this problem via a regret lower bound and provide a matching upper bound (up to log factors), thus prescribing an optimal scheme for this problem. To the best of our knowledge, our work provides the first inroad into a theoretical understanding of dynamic batch learning in high-dimensional sparse linear contextual bandits. Notably, even a special case of our result (when no batch constraint is present) yields the first minimax optimal $\tilde{O}(\sqrt{s_0T})$ regret bound for standard online learning in high-dimensional linear contextual bandits (for the no-margin case), where $s_0$ is the sparsity parameter (or an upper bound thereof) and $T$ is the learning horizon. This result (both that $\tilde{O}(\sqrt{s_0 T})$ is achievable and that $\Omega(\sqrt{s_0 T})$ is a lower bound) appears to be unknown in the emerging literature of high-dimensional contextual bandits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge