Policy Learning with Adaptively Collected Data
Paper and Code
May 05, 2021

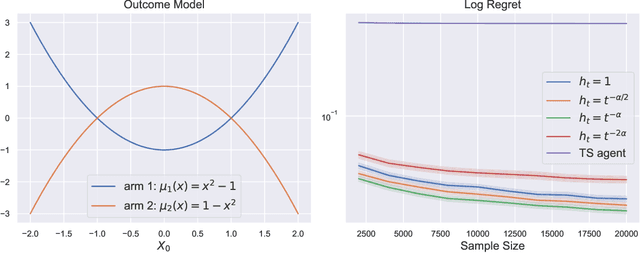

Learning optimal policies from historical data enables the gains from personalization to be realized in a wide variety of applications. The growing policy learning literature focuses on a setting where the treatment assignment policy does not adapt to the data. However, adaptive data collection is becoming more common in practice, from two primary sources: 1) data collected from adaptive experiments that are designed to improve inferential efficiency; 2) data collected from production systems that are adaptively evolving an operational policy to improve performance over time (e.g. contextual bandits). In this paper, we aim to address the challenge of learning the optimal policy with adaptively collected data and provide one of the first theoretical inquiries into this problem. We propose an algorithm based on generalized augmented inverse propensity weighted estimators and establish its finite-sample regret bound. We complement this regret upper bound with a lower bound that characterizes the fundamental difficulty of policy learning with adaptive data. Finally, we demonstrate our algorithm's effectiveness using both synthetic data and public benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge