Doubly-Adaptive Thompson Sampling for Multi-Armed and Contextual Bandits
Paper and Code
Feb 25, 2021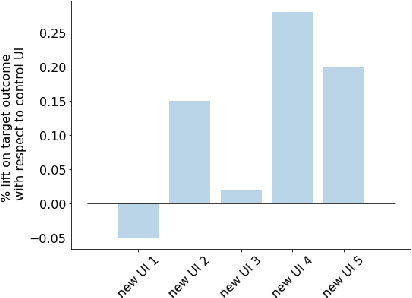
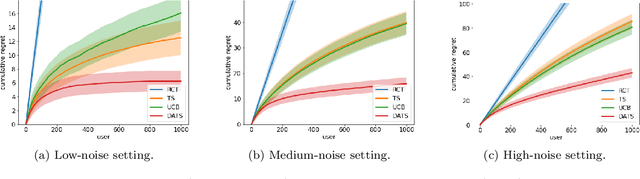
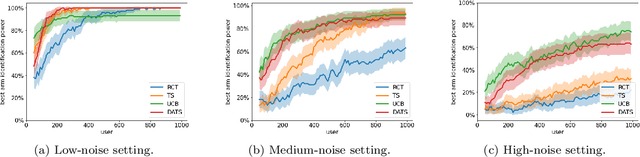
To balance exploration and exploitation, multi-armed bandit algorithms need to conduct inference on the true mean reward of each arm in every time step using the data collected so far. However, the history of arms and rewards observed up to that time step is adaptively collected and there are known challenges in conducting inference with non-iid data. In particular, sample averages, which play a prominent role in traditional upper confidence bound algorithms and traditional Thompson sampling algorithms, are neither unbiased nor asymptotically normal. We propose a variant of a Thompson sampling based algorithm that leverages recent advances in the causal inference literature and adaptively re-weighs the terms of a doubly robust estimator on the true mean reward of each arm -- hence its name doubly-adaptive Thompson sampling. The regret of the proposed algorithm matches the optimal (minimax) regret rate and its empirical evaluation in a semi-synthetic experiment based on data from a randomized control trial of a web service is performed: we see that the proposed doubly-adaptive Thompson sampling has superior empirical performance to existing baselines in terms of cumulative regret and statistical power in identifying the best arm. Further, we extend this approach to contextual bandits, where there are more sources of bias present apart from the adaptive data collection -- such as the mismatch between the true data generating process and the reward model assumptions or the unequal representations of certain regions of the context space in initial stages of learning -- and propose the linear contextual doubly-adaptive Thompson sampling and the non-parametric contextual doubly-adaptive Thompson sampling extensions of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge