How DNNs break the Curse of Dimensionality: Compositionality and Symmetry Learning

We show that deep neural networks (DNNs) can efficiently learn any composition of functions with bounded $F_{1}$-norm, which allows DNNs to break the curse of dimensionality in ways that shallow networks cannot. More specifically, we derive a generalization bound that combines a covering number argument for compositionality, and the $F_{1}$-norm (or the related Barron norm) for large width adaptivity. We show that the global minimizer of the regularized loss of DNNs can fit for example the composition of two functions $f^{*}=h\circ g$ from a small number of observations, assuming $g$ is smooth/regular and reduces the dimensionality (e.g. $g$ could be the modulo map of the symmetries of $f^{*}$), so that $h$ can be learned in spite of its low regularity. The measures of regularity we consider is the Sobolev norm with different levels of differentiability, which is well adapted to the $F_{1}$ norm. We compute scaling laws empirically and observe phase transitions depending on whether $g$ or $h$ is harder to learn, as predicted by our theory.

Which Frequencies do CNNs Need? Emergent Bottleneck Structure in Feature Learning

We describe the emergence of a Convolution Bottleneck (CBN) structure in CNNs, where the network uses its first few layers to transform the input representation into a representation that is supported only along a few frequencies and channels, before using the last few layers to map back to the outputs. We define the CBN rank, which describes the number and type of frequencies that are kept inside the bottleneck, and partially prove that the parameter norm required to represent a function $f$ scales as depth times the CBN rank $f$. We also show that the parameter norm depends at next order on the regularity of $f$. We show that any network with almost optimal parameter norm will exhibit a CBN structure in both the weights and - under the assumption that the network is stable under large learning rate - the activations, which motivates the common practice of down-sampling; and we verify that the CBN results still hold with down-sampling. Finally we use the CBN structure to interpret the functions learned by CNNs on a number of tasks.

Stochastic contextual bandits with graph feedback: from independence number to MAS number

We consider contextual bandits with graph feedback, a class of interactive learning problems with richer structures than vanilla contextual bandits, where taking an action reveals the rewards for all neighboring actions in the feedback graph under all contexts. Unlike the multi-armed bandits setting where a growing literature has painted a near-complete understanding of graph feedback, much remains unexplored in the contextual bandits counterpart. In this paper, we make inroads into this inquiry by establishing a regret lower bound $\Omega(\sqrt{\beta_M(G) T})$, where $M$ is the number of contexts, $G$ is the feedback graph, and $\beta_M(G)$ is our proposed graph-theoretical quantity that characterizes the fundamental learning limit for this class of problems. Interestingly, $\beta_M(G)$ interpolates between $\alpha(G)$ (the independence number of the graph) and $\mathsf{m}(G)$ (the maximum acyclic subgraph (MAS) number of the graph) as the number of contexts $M$ varies. We also provide algorithms that achieve near-optimal regrets for important classes of context sequences and/or feedback graphs, such as transitively closed graphs that find applications in auctions and inventory control. In particular, with many contexts, our results show that the MAS number completely characterizes the statistical complexity for contextual bandits, as opposed to the independence number in multi-armed bandits.

Coupling parameter and particle dynamics for adaptive sampling in Neural Galerkin schemes

Training nonlinear parametrizations such as deep neural networks to numerically approximate solutions of partial differential equations is often based on minimizing a loss that includes the residual, which is analytically available in limited settings only. At the same time, empirically estimating the training loss is challenging because residuals and related quantities can have high variance, especially for transport-dominated and high-dimensional problems that exhibit local features such as waves and coherent structures. Thus, estimators based on data samples from un-informed, uniform distributions are inefficient. This work introduces Neural Galerkin schemes that estimate the training loss with data from adaptive distributions, which are empirically represented via ensembles of particles. The ensembles are actively adapted by evolving the particles with dynamics coupled to the nonlinear parametrizations of the solution fields so that the ensembles remain informative for estimating the training loss. Numerical experiments indicate that few dynamic particles are sufficient for obtaining accurate empirical estimates of the training loss, even for problems with local features and with high-dimensional spatial domains.

Active operator inference for learning low-dimensional dynamical-system models from noisy data

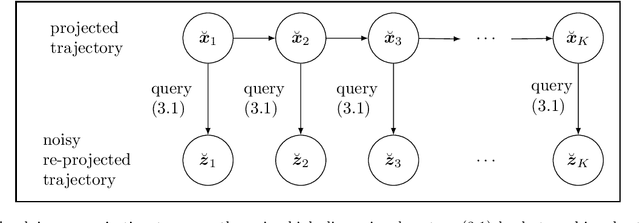
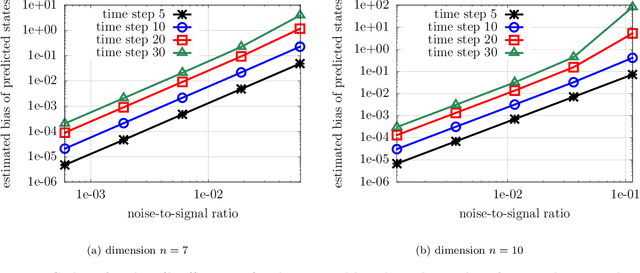
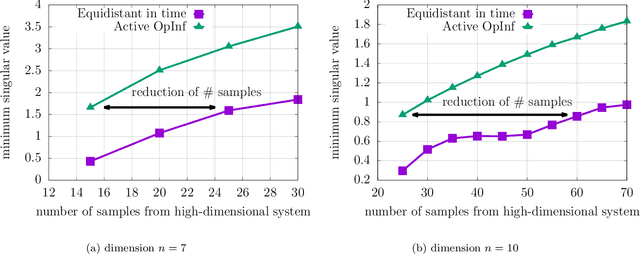
Noise poses a challenge for learning dynamical-system models because already small variations can distort the dynamics described by trajectory data. This work builds on operator inference from scientific machine learning to infer low-dimensional models from high-dimensional state trajectories polluted with noise. The presented analysis shows that, under certain conditions, the inferred operators are unbiased estimators of the well-studied projection-based reduced operators from traditional model reduction. Furthermore, the connection between operator inference and projection-based model reduction enables bounding the mean-squared errors of predictions made with the learned models with respect to traditional reduced models. The analysis also motivates an active operator inference approach that judiciously samples high-dimensional trajectories with the aim of achieving a low mean-squared error by reducing the effect of noise. Numerical experiments with high-dimensional linear and nonlinear state dynamics demonstrate that predictions obtained with active operator inference have orders of magnitude lower mean-squared errors than operator inference with traditional, equidistantly sampled trajectory data.