Polygon: Symbolic Reasoning for SQL using Conflict-Driven Under-Approximation Search

We present a novel symbolic reasoning engine for SQL which can efficiently generate an input $I$ for $n$ queries $P_1, \cdots, P_n$, such that their outputs on $I$ satisfy a given property (expressed in SMT). This is useful in different contexts, such as disproving equivalence of two SQL queries and disambiguating a set of queries. Our first idea is to reason about an under-approximation of each $P_i$ -- that is, a subset of $P_i$'s input-output behaviors. While it makes our approach both semantics-aware and lightweight, this idea alone is incomplete (as a fixed under-approximation might miss some behaviors of interest). Therefore, our second idea is to perform search over an expressive family of under-approximations (which collectively cover all program behaviors of interest), thereby making our approach complete. We have implemented these ideas in a tool, Polygon, and evaluated it on over 30,000 benchmarks across two tasks (namely, SQL equivalence refutation and query disambiguation). Our evaluation results show that Polygon significantly outperforms all prior techniques.

Active operator inference for learning low-dimensional dynamical-system models from noisy data

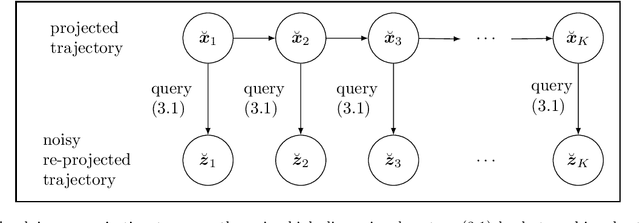
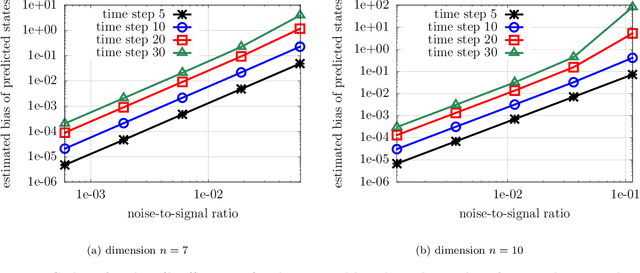
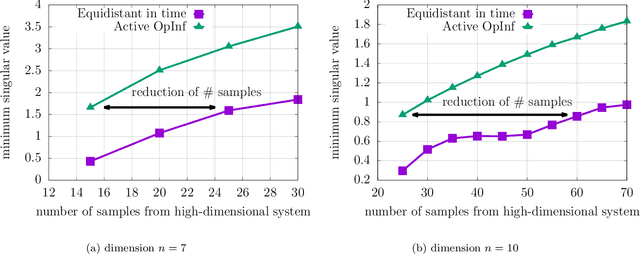
Noise poses a challenge for learning dynamical-system models because already small variations can distort the dynamics described by trajectory data. This work builds on operator inference from scientific machine learning to infer low-dimensional models from high-dimensional state trajectories polluted with noise. The presented analysis shows that, under certain conditions, the inferred operators are unbiased estimators of the well-studied projection-based reduced operators from traditional model reduction. Furthermore, the connection between operator inference and projection-based model reduction enables bounding the mean-squared errors of predictions made with the learned models with respect to traditional reduced models. The analysis also motivates an active operator inference approach that judiciously samples high-dimensional trajectories with the aim of achieving a low mean-squared error by reducing the effect of noise. Numerical experiments with high-dimensional linear and nonlinear state dynamics demonstrate that predictions obtained with active operator inference have orders of magnitude lower mean-squared errors than operator inference with traditional, equidistantly sampled trajectory data.