GenFormer: A Deep-Learning-Based Approach for Generating Multivariate Stochastic Processes

Stochastic generators are essential to produce synthetic realizations that preserve target statistical properties. We propose GenFormer, a stochastic generator for spatio-temporal multivariate stochastic processes. It is constructed using a Transformer-based deep learning model that learns a mapping between a Markov state sequence and time series values. The synthetic data generated by the GenFormer model preserves the target marginal distributions and approximately captures other desired statistical properties even in challenging applications involving a large number of spatial locations and a long simulation horizon. The GenFormer model is applied to simulate synthetic wind speed data at various stations in Florida to calculate exceedance probabilities for risk management.

Operator inference with roll outs for learning reduced models from scarce and low-quality data

Data-driven modeling has become a key building block in computational science and engineering. However, data that are available in science and engineering are typically scarce, often polluted with noise and affected by measurement errors and other perturbations, which makes learning the dynamics of systems challenging. In this work, we propose to combine data-driven modeling via operator inference with the dynamic training via roll outs of neural ordinary differential equations. Operator inference with roll outs inherits interpretability, scalability, and structure preservation of traditional operator inference while leveraging the dynamic training via roll outs over multiple time steps to increase stability and robustness for learning from low-quality and noisy data. Numerical experiments with data describing shallow water waves and surface quasi-geostrophic dynamics demonstrate that operator inference with roll outs provides predictive models from training trajectories even if data are sampled sparsely in time and polluted with noise of up to 10%.

Active operator inference for learning low-dimensional dynamical-system models from noisy data

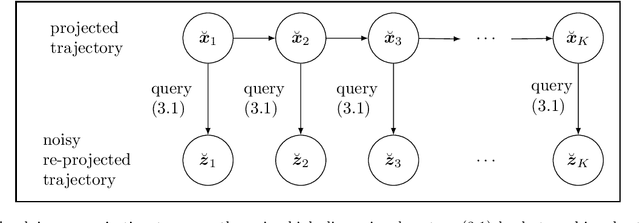
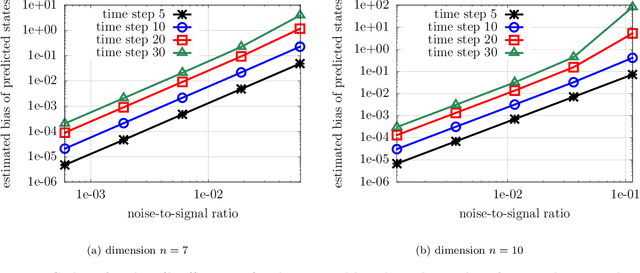
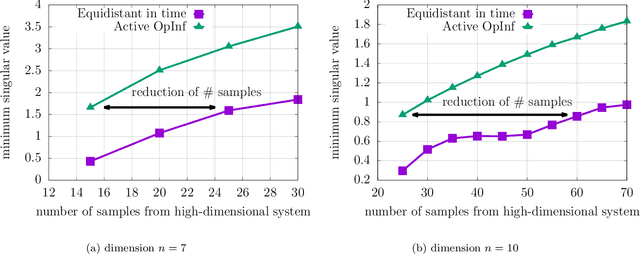
Noise poses a challenge for learning dynamical-system models because already small variations can distort the dynamics described by trajectory data. This work builds on operator inference from scientific machine learning to infer low-dimensional models from high-dimensional state trajectories polluted with noise. The presented analysis shows that, under certain conditions, the inferred operators are unbiased estimators of the well-studied projection-based reduced operators from traditional model reduction. Furthermore, the connection between operator inference and projection-based model reduction enables bounding the mean-squared errors of predictions made with the learned models with respect to traditional reduced models. The analysis also motivates an active operator inference approach that judiciously samples high-dimensional trajectories with the aim of achieving a low mean-squared error by reducing the effect of noise. Numerical experiments with high-dimensional linear and nonlinear state dynamics demonstrate that predictions obtained with active operator inference have orders of magnitude lower mean-squared errors than operator inference with traditional, equidistantly sampled trajectory data.

Operator inference of non-Markovian terms for learning reduced models from partially observed state trajectories

This work introduces a non-intrusive model reduction approach for learning reduced models from partially observed state trajectories of high-dimensional dynamical systems. The proposed approach compensates for the loss of information due to the partially observed states by constructing non-Markovian reduced models that make future-state predictions based on a history of reduced states, in contrast to traditional Markovian reduced models that rely on the current reduced state alone to predict the next state. The core contributions of this work are a data sampling scheme to sample partially observed states from high-dimensional dynamical systems and a formulation of a regression problem to fit the non-Markovian reduced terms to the sampled states. Under certain conditions, the proposed approach recovers from data the very same non-Markovian terms that one obtains with intrusive methods that require the governing equations and discrete operators of the high-dimensional dynamical system. Numerical results demonstrate that the proposed approach leads to non-Markovian reduced models that are predictive far beyond the training regime. Additionally, in the numerical experiments, the proposed approach learns non-Markovian reduced models from trajectories with only 20% observed state components that are about as accurate as traditional Markovian reduced models fitted to trajectories with 99% observed components.

Probabilistic error estimation for non-intrusive reduced models learned from data of systems governed by linear parabolic partial differential equations

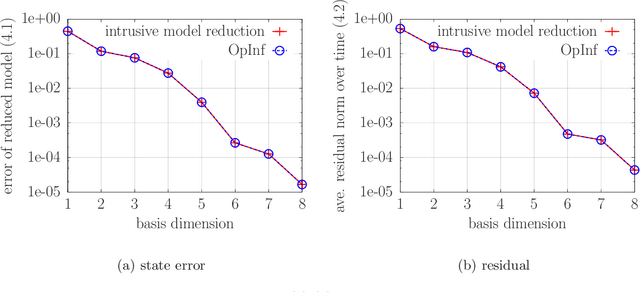
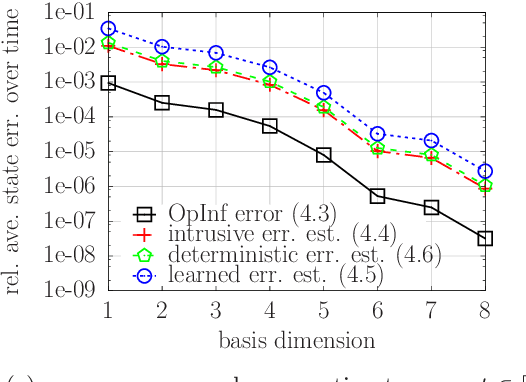
This work derives a residual-based a posteriori error estimator for reduced models learned with non-intrusive model reduction from data of high-dimensional systems governed by linear parabolic partial differential equations with control inputs. It is shown that quantities that are necessary for the error estimator can be either obtained exactly as the solutions of least-squares problems in a non-intrusive way from data such as initial conditions, control inputs, and high-dimensional solution trajectories or bounded in a probabilistic sense. The computational procedure follows an offline/online decomposition. In the offline (training) phase, the high-dimensional system is judiciously solved in a black-box fashion to generate data and to set up the error estimator. In the online phase, the estimator is used to bound the error of the reduced-model predictions for new initial conditions and new control inputs without recourse to the high-dimensional system. Numerical results demonstrate the workflow of the proposed approach from data to reduced models to certified predictions.

Time evolution of the characteristic and probability density function of diffusion processes via neural networks

We investigate the use of physics-informed neural networks-based solution of the PDE satisfied by the probability density function (pdf) of the state of a dynamical system subject to random forcing. Two alternatives for the PDE are considered: the Fokker-Planck equation and a PDE for the characteristic function (chf) of the state, both of which provide the same probabilistic information. Solving these PDEs using the finite element method is unfeasible when the dimension of the state is larger than 3. We examine analytically and numerically the advantages and disadvantages of solving the corresponding PDE of one over the other. It is also demonstrated how prior information of the dynamical system can be exploited to design and simplify the neural network architecture. Numerical examples show that: 1) the neural network solution can approximate the target solution even for partial integro-differential equations and system of PDEs, 2) solving either PDE using neural networks yields similar pdfs of the state, and 3) the solution to the PDE can be used to study the behavior of the state for different types of random forcings.