Transported Memory Networks accelerating Computational Fluid Dynamics

In recent years, augmentation of differentiable PDE solvers with neural networks has shown promising results, particularly in fluid simulations. However, most approaches rely on convolutional neural networks and custom solvers operating on Cartesian grids with efficient access to cell data. This particular choice poses challenges for industrial-grade solvers that operate on unstructured meshes, where access is restricted to neighboring cells only. In this work, we address this limitation using a novel architecture, named Transported Memory Networks. The architecture draws inspiration from both traditional turbulence models and recurrent neural networks, and it is fully compatible with generic discretizations. Our results show that it is point-wise and statistically comparable to, or improves upon, previous methods in terms of both accuracy and computational efficiency.

Operator inference with roll outs for learning reduced models from scarce and low-quality data

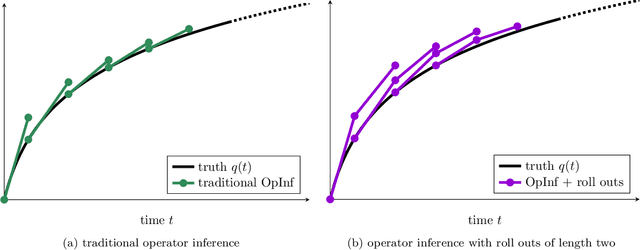
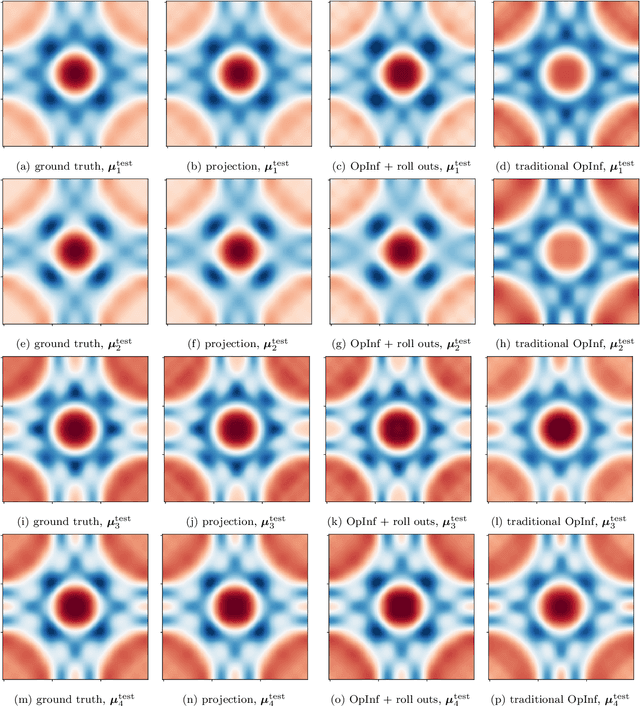
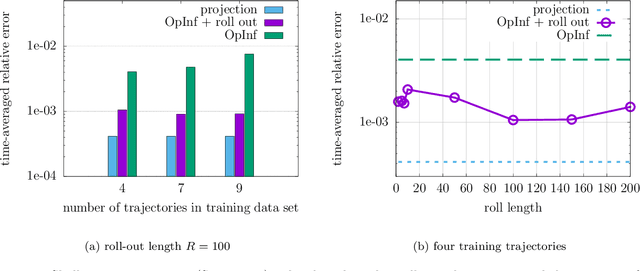
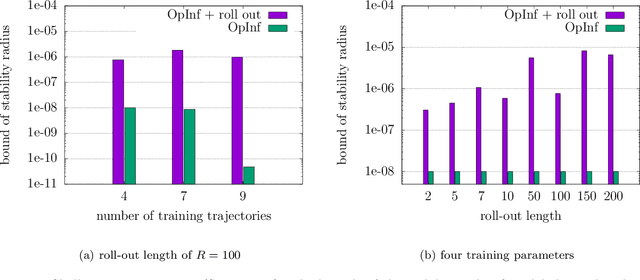
Data-driven modeling has become a key building block in computational science and engineering. However, data that are available in science and engineering are typically scarce, often polluted with noise and affected by measurement errors and other perturbations, which makes learning the dynamics of systems challenging. In this work, we propose to combine data-driven modeling via operator inference with the dynamic training via roll outs of neural ordinary differential equations. Operator inference with roll outs inherits interpretability, scalability, and structure preservation of traditional operator inference while leveraging the dynamic training via roll outs over multiple time steps to increase stability and robustness for learning from low-quality and noisy data. Numerical experiments with data describing shallow water waves and surface quasi-geostrophic dynamics demonstrate that operator inference with roll outs provides predictive models from training trajectories even if data are sampled sparsely in time and polluted with noise of up to 10%.

Active-learning-based non-intrusive Model Order Reduction

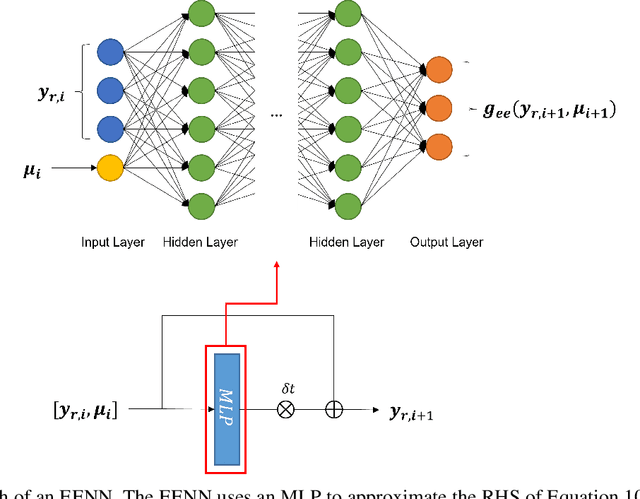
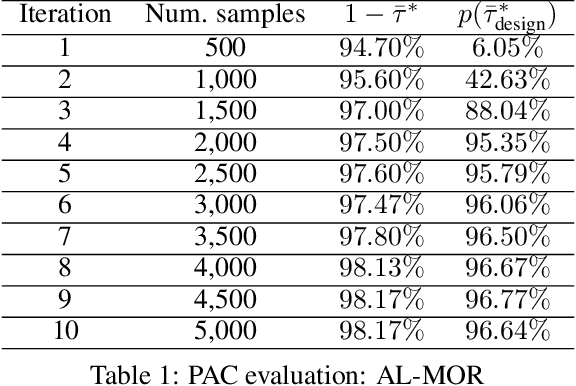
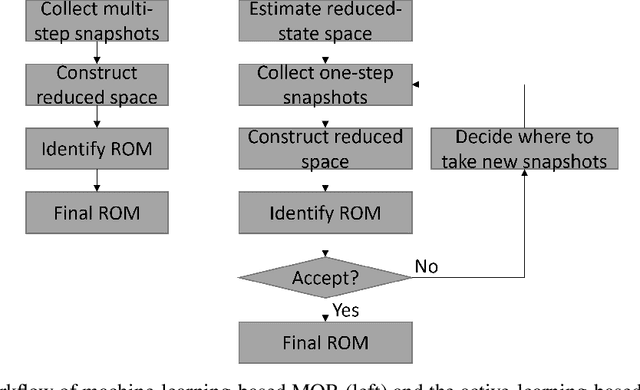
The Model Order Reduction (MOR) technique can provide compact numerical models for fast simulation. Different from the intrusive MOR methods, the non-intrusive MOR does not require access to the Full Order Models (FOMs), especially system matrices. Since the non-intrusive MOR methods strongly rely on the snapshots of the FOMs, constructing good snapshot sets becomes crucial. In this work, we propose a new active learning approach with two novelties. A novel idea with our approach is the use of single-time step snapshots from the system states taken from an estimation of the reduced-state space. These states are selected using a greedy strategy supported by an error estimator based Gaussian Process Regression (GPR). Additionally, we introduce a use case-independent validation strategy based on Probably Approximately Correct (PAC) learning. In this work, we use Artificial Neural Networks (ANNs) to identify the Reduced Order Model (ROM), however the method could be similarly applied to other ROM identification methods. The performance of the whole workflow is tested by a 2-D thermal conduction and a 3-D vacuum furnace model. With little required user interaction and a training strategy independent to a specific use case, the proposed method offers a huge potential for industrial usage to create so-called executable Digital Twins (DTs).

Model Order Reduction based on Runge-Kutta Neural Network

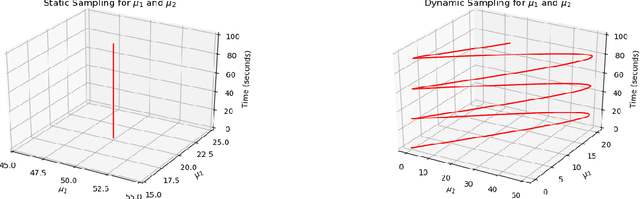
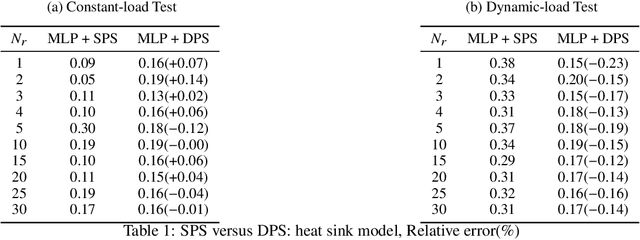
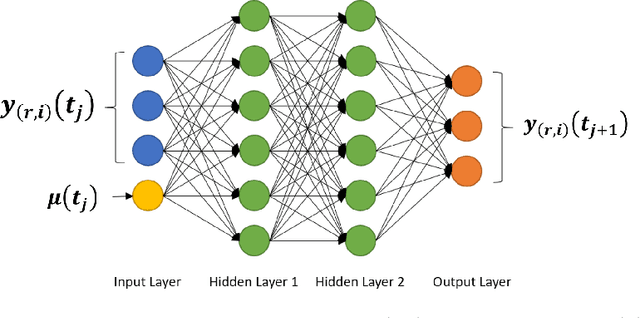
Model Order Reduction (MOR) methods enable the generation of real-time-capable digital twins, which can enable various novel value streams in industry. While traditional projection-based methods are robust and accurate for linear problems, incorporating Machine Learning to deal with nonlinearity becomes a new choice for reducing complex problems. Such methods usually consist of two steps. The first step is dimension reduction by projection-based method, and the second is the model reconstruction by Neural Network. In this work, we apply some modifications for both steps respectively and investigate how they are impacted by testing with three simulation models. In all cases Proper Orthogonal Decomposition (POD) is used for dimension reduction. For this step, the effects of generating the input snapshot database with constant input parameters is compared with time-dependent input parameters. For the model reconstruction step, two types of neural network architectures are compared: Multilayer Perceptron (MLP) and Runge-Kutta Neural Network (RKNN). The MLP learns the system state directly while RKNN learns the derivative of system state and predicts the new state as a Runge-Kutta integrator.

Machine Learning-Based Optimal Mesh Generation in Computational Fluid Dynamics

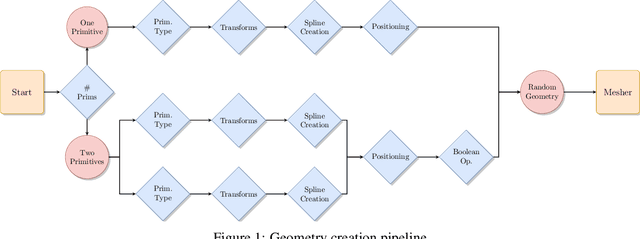
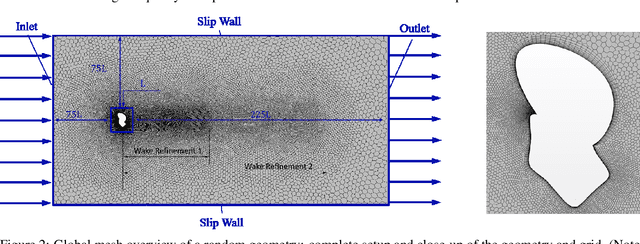
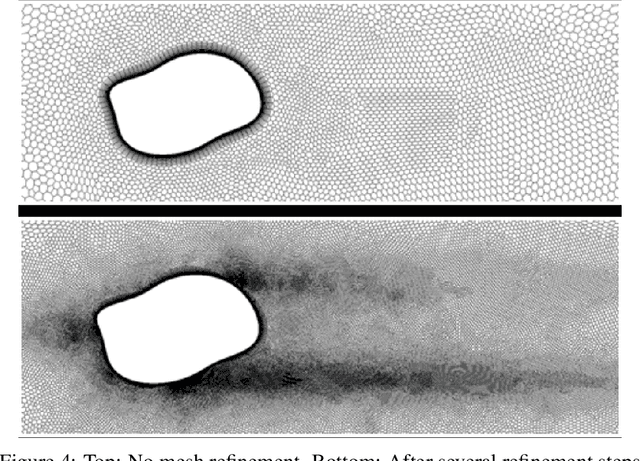
Computational Fluid Dynamics (CFD) is a major sub-field of engineering. Corresponding flow simulations are typically characterized by heavy computational resource requirements. Often, very fine and complex meshes are required to resolve physical effects in an appropriate manner. Since all CFD algorithms scale at least linearly with the size of the underlying mesh discretization, finding an optimal mesh is key for computational efficiency. One methodology used to find optimal meshes is goal-oriented adaptive mesh refinement. However, this is typically computationally demanding and only available in a limited number of tools. Within this contribution, we adopt a machine learning approach to identify optimal mesh densities. We generate optimized meshes using classical methodologies and propose to train a convolutional network predicting optimal mesh densities given arbitrary geometries. The proposed concept is validated along 2d wind tunnel simulations with more than 60,000 simulations. Using a training set of 20,000 simulations we achieve accuracies of more than 98.7%. Corresponding predictions of optimal meshes can be used as input for any mesh generation and CFD tool. Thus without complex computations, any CFD engineer can start his predictions from a high quality mesh.