Bellman Optimality of Average-Reward Robust Markov Decision Processes with a Constant Gain

Learning and optimal control under robust Markov decision processes (MDPs) have received increasing attention, yet most existing theory, algorithms, and applications focus on finite-horizon or discounted models. The average-reward formulation, while natural in many operations research and management contexts, remains underexplored. This is primarily because the dynamic programming foundations are technically challenging and only partially understood, with several fundamental questions remaining open. This paper steps toward a general framework for average-reward robust MDPs by analyzing the constant-gain setting. We study the average-reward robust control problem with possible information asymmetries between the controller and an S-rectangular adversary. Our analysis centers on the constant-gain robust Bellman equation, examining both the existence of solutions and their relationship to the optimal average reward. Specifically, we identify when solutions to the robust Bellman equation characterize the optimal average reward and stationary policies, and we provide sufficient conditions ensuring solutions' existence. These findings expand the dynamic programming theory for average-reward robust MDPs and lay a foundation for robust dynamic decision making under long-run average criteria in operational environments.

Representation-Aware Distributionally Robust Optimization: A Knowledge Transfer Framework

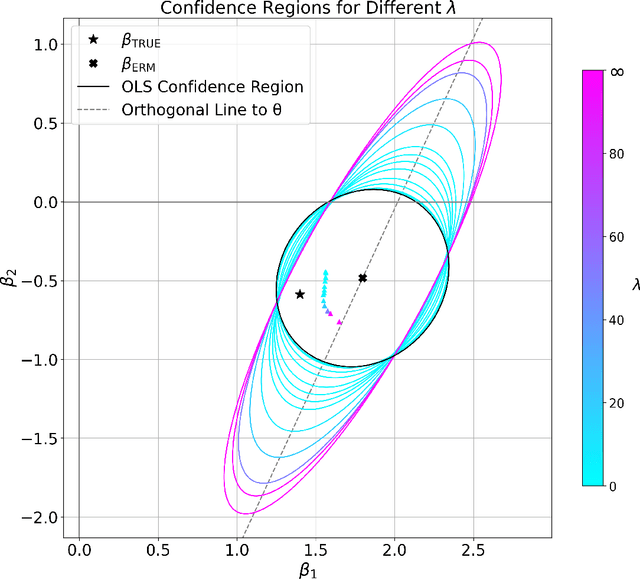
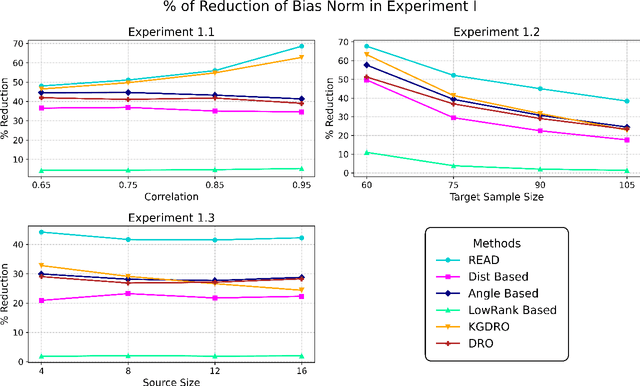
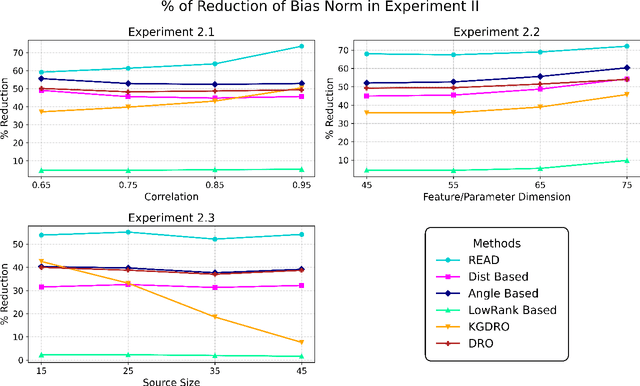
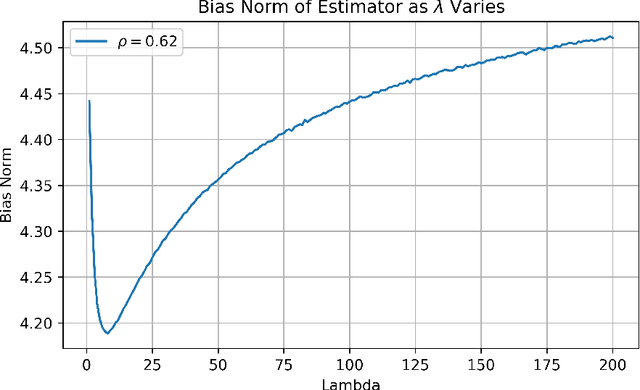
We propose REpresentation-Aware Distributionally Robust Estimation (READ), a novel framework for Wasserstein distributionally robust learning that accounts for predictive representations when guarding against distributional shifts. Unlike classical approaches that treat all feature perturbations equally, READ embeds a multidimensional alignment parameter into the transport cost, allowing the model to differentially discourage perturbations along directions associated with informative representations. This yields robustness to feature variation while preserving invariant structure. Our first contribution is a theoretical foundation: we show that seminorm regularizations for linear regression and binary classification arise as Wasserstein distributionally robust objectives, thereby providing tractable reformulations of READ and unifying a broad class of regularized estimators under the DRO lens. Second, we adopt a principled procedure for selecting the Wasserstein radius using the techniques of robust Wasserstein profile inference. This further enables the construction of valid, representation-aware confidence regions for model parameters with distinct geometric features. Finally, we analyze the geometry of READ estimators as the alignment parameters vary and propose an optimization algorithm to estimate the projection of the global optimum onto this solution surface. This procedure selects among equally robust estimators while optimally constructing a representation structure. We conclude by demonstrating the effectiveness of our framework through extensive simulations and a real-world study, providing a powerful robust estimation grounded in learning representation.

Near-Optimal Sample Complexities of Divergence-based S-rectangular Distributionally Robust Reinforcement Learning

Distributionally robust reinforcement learning (DR-RL) has recently gained significant attention as a principled approach that addresses discrepancies between training and testing environments. To balance robustness, conservatism, and computational traceability, the literature has introduced DR-RL models with SA-rectangular and S-rectangular adversaries. While most existing statistical analyses focus on SA-rectangular models, owing to their algorithmic simplicity and the optimality of deterministic policies, S-rectangular models more accurately capture distributional discrepancies in many real-world applications and often yield more effective robust randomized policies. In this paper, we study the empirical value iteration algorithm for divergence-based S-rectangular DR-RL and establish near-optimal sample complexity bounds of $\widetilde{O}(|\mathcal{S}||\mathcal{A}|(1-\gamma)^{-4}\varepsilon^{-2})$, where $\varepsilon$ is the target accuracy, $|\mathcal{S}|$ and $|\mathcal{A}|$ denote the cardinalities of the state and action spaces, and $\gamma$ is the discount factor. To the best of our knowledge, these are the first sample complexity results for divergence-based S-rectangular models that achieve optimal dependence on $|\mathcal{S}|$, $|\mathcal{A}|$, and $\varepsilon$ simultaneously. We further validate this theoretical dependence through numerical experiments on a robust inventory control problem and a theoretical worst-case example, demonstrating the fast learning performance of our proposed algorithm.

Sample Complexity of Distributionally Robust Average-Reward Reinforcement Learning

Motivated by practical applications where stable long-term performance is critical-such as robotics, operations research, and healthcare-we study the problem of distributionally robust (DR) average-reward reinforcement learning. We propose two algorithms that achieve near-optimal sample complexity. The first reduces the problem to a DR discounted Markov decision process (MDP), while the second, Anchored DR Average-Reward MDP, introduces an anchoring state to stabilize the controlled transition kernels within the uncertainty set. Assuming the nominal MDP is uniformly ergodic, we prove that both algorithms attain a sample complexity of $\widetilde{O}\left(|\mathbf{S}||\mathbf{A}| t_{\mathrm{mix}}^2\varepsilon^{-2}\right)$ for estimating the optimal policy as well as the robust average reward under KL and $f_k$-divergence-based uncertainty sets, provided the uncertainty radius is sufficiently small. Here, $\varepsilon$ is the target accuracy, $|\mathbf{S}|$ and $|\mathbf{A}|$ denote the sizes of the state and action spaces, and $t_{\mathrm{mix}}$ is the mixing time of the nominal MDP. This represents the first finite-sample convergence guarantee for DR average-reward reinforcement learning. We further validate the convergence rates of our algorithms through numerical experiments.

Knowledge-Guided Wasserstein Distributionally Robust Optimization

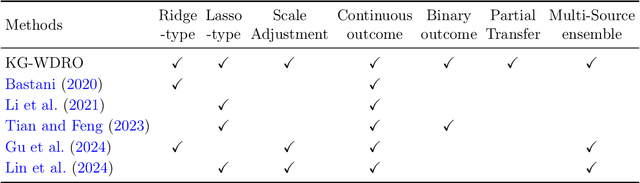
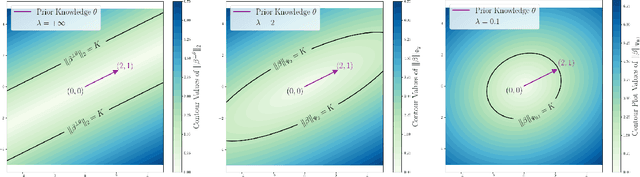
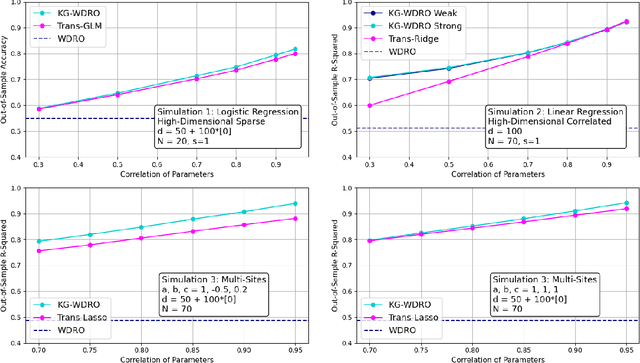
Transfer learning is a popular strategy to leverage external knowledge and improve statistical efficiency, particularly with a limited target sample. We propose a novel knowledge-guided Wasserstein Distributionally Robust Optimization (KG-WDRO) framework that adaptively incorporates multiple sources of external knowledge to overcome the conservativeness of vanilla WDRO, which often results in overly pessimistic shrinkage toward zero. Our method constructs smaller Wasserstein ambiguity sets by controlling the transportation along directions informed by the source knowledge. This strategy can alleviate perturbations on the predictive projection of the covariates and protect against information loss. Theoretically, we establish the equivalence between our WDRO formulation and the knowledge-guided shrinkage estimation based on collinear similarity, ensuring tractability and geometrizing the feasible set. This also reveals a novel and general interpretation for recent shrinkage-based transfer learning approaches from the perspective of distributional robustness. In addition, our framework can adjust for scaling differences in the regression models between the source and target and accommodates general types of regularization such as lasso and ridge. Extensive simulations demonstrate the superior performance and adaptivity of KG-WDRO in enhancing small-sample transfer learning.

ScoreFusion: fusing score-based generative models via Kullback-Leibler barycenters

We study the problem of fusing pre-trained (auxiliary) generative models to enhance the training of a target generative model. We propose using KL-divergence weighted barycenters as an optimal fusion mechanism, in which the barycenter weights are optimally trained to minimize a suitable loss for the target population. While computing the optimal KL-barycenter weights can be challenging, we demonstrate that this process can be efficiently executed using diffusion score training when the auxiliary generative models are also trained based on diffusion score methods. Moreover, we show that our fusion method has a dimension-free sample complexity in total variation distance provided that the auxiliary models are well fitted for their own task and the auxiliary tasks combined capture the target well. The main takeaway of our method is that if the auxiliary models are well-trained and can borrow features from each other that are present in the target, our fusion method significantly improves the training of generative models. We provide a concise computational implementation of the fusion algorithm, and validate its efficiency in the low-data regime with numerical experiments involving mixtures models and image datasets.

Statistical Learning of Distributionally Robust Stochastic Control in Continuous State Spaces

We explore the control of stochastic systems with potentially continuous state and action spaces, characterized by the state dynamics $X_{t+1} = f(X_t, A_t, W_t)$. Here, $X$, $A$, and $W$ represent the state, action, and exogenous random noise processes, respectively, with $f$ denoting a known function that describes state transitions. Traditionally, the noise process $\{W_t, t \geq 0\}$ is assumed to be independent and identically distributed, with a distribution that is either fully known or can be consistently estimated. However, the occurrence of distributional shifts, typical in engineering settings, necessitates the consideration of the robustness of the policy. This paper introduces a distributionally robust stochastic control paradigm that accommodates possibly adaptive adversarial perturbation to the noise distribution within a prescribed ambiguity set. We examine two adversary models: current-action-aware and current-action-unaware, leading to different dynamic programming equations. Furthermore, we characterize the optimal finite sample minimax rates for achieving uniform learning of the robust value function across continuum states under both adversary types, considering ambiguity sets defined by $f_k$-divergence and Wasserstein distance. Finally, we demonstrate the applicability of our framework across various real-world settings.

Calibration-then-Calculation: A Variance Reduced Metric Framework in Deep Click-Through Rate Prediction Models

Deep learning has been widely adopted across various fields, but there has been little focus on evaluating the performance of deep learning pipelines. With the increased use of large datasets and complex models, it has become common to run the training process only once and compare the result to previous benchmarks. However, this procedure can lead to imprecise comparisons due to the variance in neural network evaluation metrics. The metric variance comes from the randomness inherent in the training process of deep learning pipelines. Traditional solutions such as running the training process multiple times are usually not feasible in deep learning due to computational limitations. In this paper, we propose a new metric framework, Calibrated Loss Metric, that addresses this issue by reducing the variance in its vanilla counterpart. As a result, the new metric has a higher accuracy to detect effective modeling improvement. Our approach is supported by theoretical justifications and extensive experimental validations in the context of Deep Click-Through Rate Prediction Models.

Seller-Side Experiments under Interference Induced by Feedback Loops in Two-Sided Platforms

Two-sided platforms are central to modern commerce and content sharing and often utilize A/B testing for developing new features. While user-side experiments are common, seller-side experiments become crucial for specific interventions and metrics. This paper investigates the effects of interference caused by feedback loops on seller-side experiments in two-sided platforms, with a particular focus on the counterfactual interleaving design, proposed in \citet{ha2020counterfactual,nandy2021b}. These feedback loops, often generated by pacing algorithms, cause outcomes from earlier sessions to influence subsequent ones. This paper contributes by creating a mathematical framework to analyze this interference, theoretically estimating its impact, and conducting empirical evaluations of the counterfactual interleaving design in real-world scenarios. Our research shows that feedback loops can result in misleading conclusions about the treatment effects.

On the Foundation of Distributionally Robust Reinforcement Learning

Motivated by the need for a robust policy in the face of environment shifts between training and the deployment, we contribute to the theoretical foundation of distributionally robust reinforcement learning (DRRL). This is accomplished through a comprehensive modeling framework centered around distributionally robust Markov decision processes (DRMDPs). This framework obliges the decision maker to choose an optimal policy under the worst-case distributional shift orchestrated by an adversary. By unifying and extending existing formulations, we rigorously construct DRMDPs that embraces various modeling attributes for both the decision maker and the adversary. These attributes include adaptability granularity, exploring history-dependent, Markov, and Markov time-homogeneous decision maker and adversary dynamics. Additionally, we delve into the flexibility of shifts induced by the adversary, examining SA and S-rectangularity. Within this DRMDP framework, we investigate conditions for the existence or absence of the dynamic programming principle (DPP). From an algorithmic standpoint, the existence of DPP holds significant implications, as the vast majority of existing data and computationally efficiency RL algorithms are reliant on the DPP. To study its existence, we comprehensively examine combinations of controller and adversary attributes, providing streamlined proofs grounded in a unified methodology. We also offer counterexamples for settings in which a DPP with full generality is absent.