Can LLMs Clean Up Your Mess? A Survey of Application-Ready Data Preparation with LLMs

Data preparation aims to denoise raw datasets, uncover cross-dataset relationships, and extract valuable insights from them, which is essential for a wide range of data-centric applications. Driven by (i) rising demands for application-ready data (e.g., for analytics, visualization, decision-making), (ii) increasingly powerful LLM techniques, and (iii) the emergence of infrastructures that facilitate flexible agent construction (e.g., using Databricks Unity Catalog), LLM-enhanced methods are rapidly becoming a transformative and potentially dominant paradigm for data preparation. By investigating hundreds of recent literature works, this paper presents a systematic review of this evolving landscape, focusing on the use of LLM techniques to prepare data for diverse downstream tasks. First, we characterize the fundamental paradigm shift, from rule-based, model-specific pipelines to prompt-driven, context-aware, and agentic preparation workflows. Next, we introduce a task-centric taxonomy that organizes the field into three major tasks: data cleaning (e.g., standardization, error processing, imputation), data integration (e.g., entity matching, schema matching), and data enrichment (e.g., data annotation, profiling). For each task, we survey representative techniques, and highlight their respective strengths (e.g., improved generalization, semantic understanding) and limitations (e.g., the prohibitive cost of scaling LLMs, persistent hallucinations even in advanced agents, the mismatch between advanced methods and weak evaluation). Moreover, we analyze commonly used datasets and evaluation metrics (the empirical part). Finally, we discuss open research challenges and outline a forward-looking roadmap that emphasizes scalable LLM-data systems, principled designs for reliable agentic workflows, and robust evaluation protocols.

DynaDebate: Breaking Homogeneity in Multi-Agent Debate with Dynamic Path Generation

Recent years have witnessed the rapid development of Large Language Model-based Multi-Agent Systems (MAS), which excel at collaborative decision-making and complex problem-solving. Recently, researchers have further investigated Multi-Agent Debate (MAD) frameworks, which enhance the reasoning and collaboration capabilities of MAS through information exchange and debate among multiple agents. However, existing approaches often rely on unguided initialization, causing agents to adopt identical reasoning paths that lead to the same errors. As a result, effective debate among agents is hindered, and the final outcome frequently degenerates into simple majority voting. To solve the above problem, in this paper, we introduce Dynamic Multi-Agent Debate (DynaDebate), which enhances the effectiveness of multi-agent debate through three key mechanisms: (1) Dynamic Path Generation and Allocation, which employs a dedicated Path Generation Agent to generate diverse and logical solution paths with adaptive redundancy; (2) Process-Centric Debate, which shifts the focus from surface-level outcome voting to rigorous step-by-step logic critique to ensure process correctness; (3) A Trigger-Based Verification Agent, which is activated upon disagreement and uses external tools to objectively resolve deadlocks. Extensive experiments demonstrate that DynaDebate achieves superior performance across various benchmarks, surpassing existing state-of-the-art MAD methods.

A Nonparametric Statistics Approach to Feature Selection in Deep Neural Networks with Theoretical Guarantees

This paper tackles the problem of feature selection in a highly challenging setting: $\mathbb{E}(y | \boldsymbol{x}) = G(\boldsymbol{x}_{\mathcal{S}_0})$, where $\mathcal{S}_0$ is the set of relevant features and $G$ is an unknown, potentially nonlinear function subject to mild smoothness conditions. Our approach begins with feature selection in deep neural networks, then generalizes the results to H{ö}lder smooth functions by exploiting the strong approximation capabilities of neural networks. Unlike conventional optimization-based deep learning methods, we reformulate neural networks as index models and estimate $\mathcal{S}_0$ using the second-order Stein's formula. This gradient-descent-free strategy guarantees feature selection consistency with a sample size requirement of $n = Ω(p^2)$, where $p$ is the feature dimension. To handle high-dimensional scenarios, we further introduce a screening-and-selection mechanism that achieves nonlinear selection consistency when $n = Ω(s \log p)$, with $s$ representing the sparsity level. Additionally, we refit a neural network on the selected features for prediction and establish performance guarantees under a relaxed sparsity assumption. Extensive simulations and real-data analyses demonstrate the strong performance of our method even in the presence of complex feature interactions.

SUSEP-Net: Simulation-Supervised and Contrastive Learning-based Deep Neural Networks for Susceptibility Source Separation

Quantitative susceptibility mapping (QSM) provides a valuable tool for quantifying susceptibility distributions in human brains; however, two types of opposing susceptibility sources (i.e., paramagnetic and diamagnetic), may coexist in a single voxel, and cancel each other out in net QSM images. Susceptibility source separation techniques enable the extraction of sub-voxel information from QSM maps. This study proposes a novel SUSEP-Net for susceptibility source separation by training a dual-branch U-net with a simulation-supervised training strategy. In addition, a contrastive learning framework is included to explicitly impose similarity-based constraints between the branch-specific guidance features in specially-designed encoders and the latent features in the decoders. Comprehensive experiments were carried out on both simulated and in vivo data, including healthy subjects and patients with pathological conditions, to compare SUSEP-Net with three state-of-the-art susceptibility source separation methods (i.e., APART-QSM, \c{hi}-separation, and \c{hi}-sepnet). SUSEP-Net consistently showed improved results compared with the other three methods, with better numerical metrics, improved high-intensity hemorrhage and calcification lesion contrasts, and reduced artifacts in brains with pathological conditions. In addition, experiments on an agarose gel phantom data were conducted to validate the accuracy and the generalization capability of SUSEP-Net.

SUFFICIENT: A scan-specific unsupervised deep learning framework for high-resolution 3D isotropic fetal brain MRI reconstruction

High-quality 3D fetal brain MRI reconstruction from motion-corrupted 2D slices is crucial for clinical diagnosis. Reliable slice-to-volume registration (SVR)-based motion correction and super-resolution reconstruction (SRR) methods are essential. Deep learning (DL) has demonstrated potential in enhancing SVR and SRR when compared to conventional methods. However, it requires large-scale external training datasets, which are difficult to obtain for clinical fetal MRI. To address this issue, we propose an unsupervised iterative SVR-SRR framework for isotropic HR volume reconstruction. Specifically, SVR is formulated as a function mapping a 2D slice and a 3D target volume to a rigid transformation matrix, which aligns the slice to the underlying location in the target volume. The function is parameterized by a convolutional neural network, which is trained by minimizing the difference between the volume slicing at the predicted position and the input slice. In SRR, a decoding network embedded within a deep image prior framework is incorporated with a comprehensive image degradation model to produce the high-resolution (HR) volume. The deep image prior framework offers a local consistency prior to guide the reconstruction of HR volumes. By performing a forward degradation model, the HR volume is optimized by minimizing loss between predicted slices and the observed slices. Comprehensive experiments conducted on large-magnitude motion-corrupted simulation data and clinical data demonstrate the superior performance of the proposed framework over state-of-the-art fetal brain reconstruction frameworks.

Near-Optimal Sample Complexities of Divergence-based S-rectangular Distributionally Robust Reinforcement Learning

Distributionally robust reinforcement learning (DR-RL) has recently gained significant attention as a principled approach that addresses discrepancies between training and testing environments. To balance robustness, conservatism, and computational traceability, the literature has introduced DR-RL models with SA-rectangular and S-rectangular adversaries. While most existing statistical analyses focus on SA-rectangular models, owing to their algorithmic simplicity and the optimality of deterministic policies, S-rectangular models more accurately capture distributional discrepancies in many real-world applications and often yield more effective robust randomized policies. In this paper, we study the empirical value iteration algorithm for divergence-based S-rectangular DR-RL and establish near-optimal sample complexity bounds of $\widetilde{O}(|\mathcal{S}||\mathcal{A}|(1-\gamma)^{-4}\varepsilon^{-2})$, where $\varepsilon$ is the target accuracy, $|\mathcal{S}|$ and $|\mathcal{A}|$ denote the cardinalities of the state and action spaces, and $\gamma$ is the discount factor. To the best of our knowledge, these are the first sample complexity results for divergence-based S-rectangular models that achieve optimal dependence on $|\mathcal{S}|$, $|\mathcal{A}|$, and $\varepsilon$ simultaneously. We further validate this theoretical dependence through numerical experiments on a robust inventory control problem and a theoretical worst-case example, demonstrating the fast learning performance of our proposed algorithm.

Ustnlp16 at SemEval-2025 Task 9: Improving Model Performance through Imbalance Handling and Focal Loss

Classification tasks often suffer from imbal- anced data distribution, which presents chal- lenges in food hazard detection due to severe class imbalances, short and unstructured text, and overlapping semantic categories. In this paper, we present our system for SemEval- 2025 Task 9: Food Hazard Detection, which ad- dresses these issues by applying data augmenta- tion techniques to improve classification perfor- mance. We utilize transformer-based models, BERT and RoBERTa, as backbone classifiers and explore various data balancing strategies, including random oversampling, Easy Data Augmentation (EDA), and focal loss. Our ex- periments show that EDA effectively mitigates class imbalance, leading to significant improve- ments in accuracy and F1 scores. Furthermore, combining focal loss with oversampling and EDA further enhances model robustness, par- ticularly for hard-to-classify examples. These findings contribute to the development of more effective NLP-based classification models for food hazard detection.

Jointly RS Image Deblurring and Super-Resolution with Adjustable-Kernel and Multi-Domain Attention

Remote Sensing (RS) image deblurring and Super-Resolution (SR) are common tasks in computer vision that aim at restoring RS image detail and spatial scale, respectively. However, real-world RS images often suffer from a complex combination of global low-resolution (LR) degeneration and local blurring degeneration. Although carefully designed deblurring and SR models perform well on these two tasks individually, a unified model that performs jointly RS image deblurring and super-resolution (JRSIDSR) task is still challenging due to the vital dilemma of reconstructing the global and local degeneration simultaneously. Additionally, existing methods struggle to capture the interrelationship between deblurring and SR processes, leading to suboptimal results. To tackle these issues, we give a unified theoretical analysis of RS images' spatial and blur degeneration processes and propose a dual-branch parallel network named AKMD-Net for the JRSIDSR task. AKMD-Net consists of two main branches: deblurring and super-resolution branches. In the deblurring branch, we design a pixel-adjustable kernel block (PAKB) to estimate the local and spatial-varying blur kernels. In the SR branch, a multi-domain attention block (MDAB) is proposed to capture the global contextual information enhanced with high-frequency details. Furthermore, we develop an adaptive feature fusion (AFF) module to model the contextual relationships between the deblurring and SR branches. Finally, we design an adaptive Wiener loss (AW Loss) to depress the prior noise in the reconstructed images. Extensive experiments demonstrate that the proposed AKMD-Net achieves state-of-the-art (SOTA) quantitative and qualitative performance on commonly used RS image datasets. The source code is publicly available at https://github.com/zpc456/AKMD-Net.

Time Series Generative Learning with Application to Brain Imaging Analysis

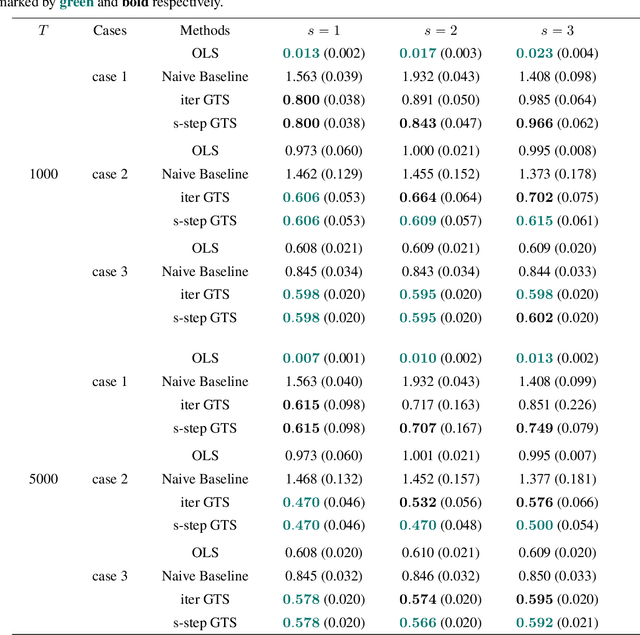
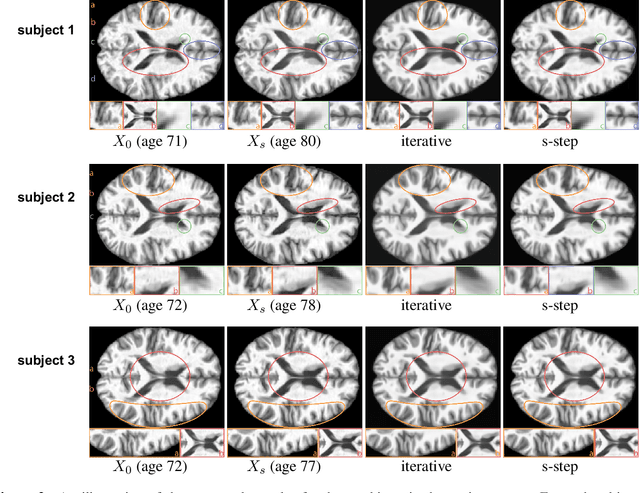
This paper focuses on the analysis of sequential image data, particularly brain imaging data such as MRI, fMRI, CT, with the motivation of understanding the brain aging process and neurodegenerative diseases. To achieve this goal, we investigate image generation in a time series context. Specifically, we formulate a min-max problem derived from the $f$-divergence between neighboring pairs to learn a time series generator in a nonparametric manner. The generator enables us to generate future images by transforming prior lag-k observations and a random vector from a reference distribution. With a deep neural network learned generator, we prove that the joint distribution of the generated sequence converges to the latent truth under a Markov and a conditional invariance condition. Furthermore, we extend our generation mechanism to a panel data scenario to accommodate multiple samples. The effectiveness of our mechanism is evaluated by generating real brain MRI sequences from the Alzheimer's Disease Neuroimaging Initiative. These generated image sequences can be used as data augmentation to enhance the performance of further downstream tasks, such as Alzheimer's disease detection.

Deep Residual Networks with a Fully Connected Recon-struction Layer for Single Image Super-Resolution

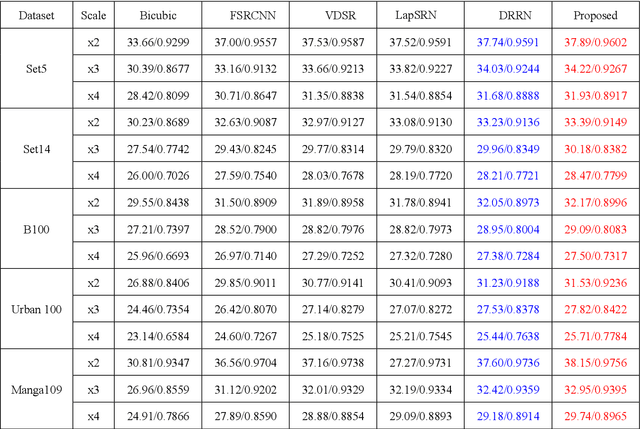
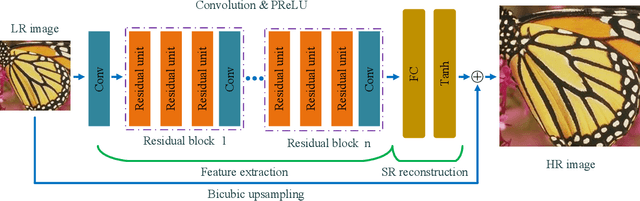
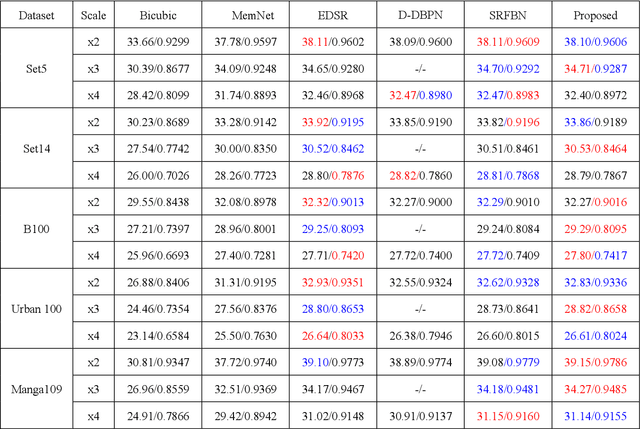
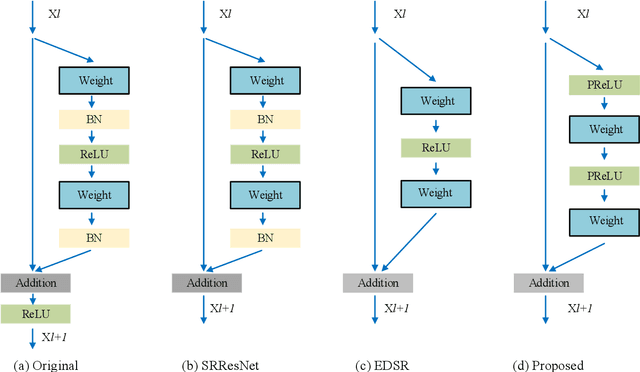
Recently, deep neural networks have achieved impressive performance in terms of both reconstruction accuracy and efficiency for single image super-resolution (SISR). However, the network model of these methods is a fully convolutional neural network, which is limit to exploit contextual information over the global region of the input image. In this paper, we discuss a new SR architecture where features are extracted in the low-resolution (LR) space, and then we use a fully connected layer which learns an array of upsampling weights to reconstruct the desired high-resolution (HR) image from the final LR features. By doing so, we effectively exploit global context information over the input image region, whilst maintaining the low computational complexity for the overall SR operation. In addition, we introduce an edge difference constraint into our loss function to pre-serve edges and texture structures. Extensive experiments validate that our meth-od outperforms the existing state-of-the-art methods