Nonlinear Multiple Response Regression and Learning of Latent Spaces

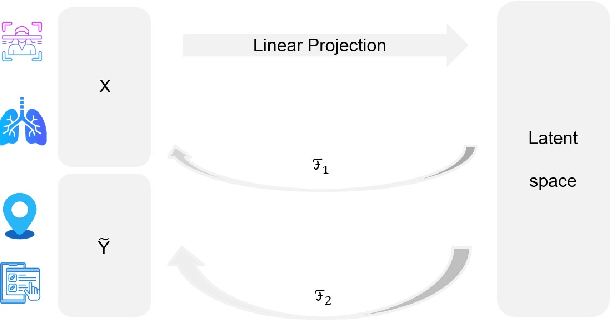
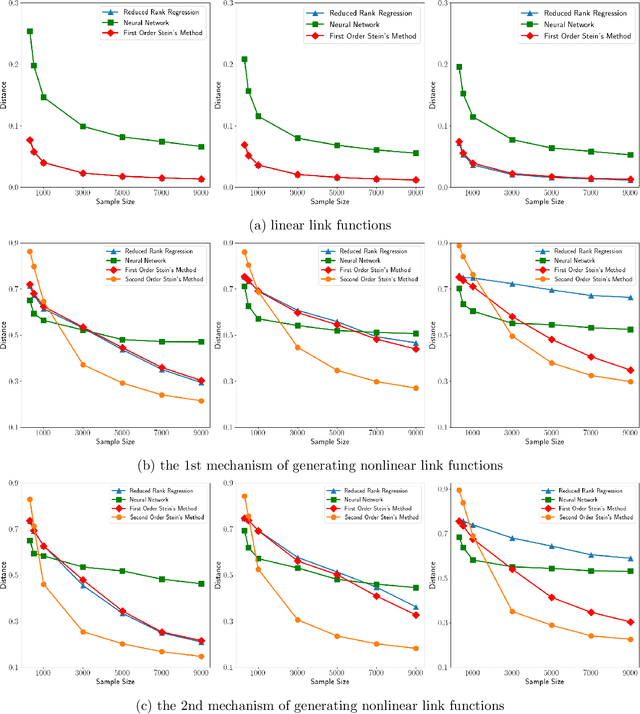
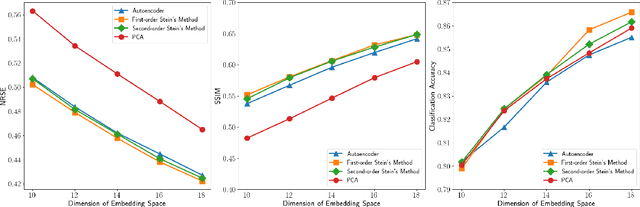
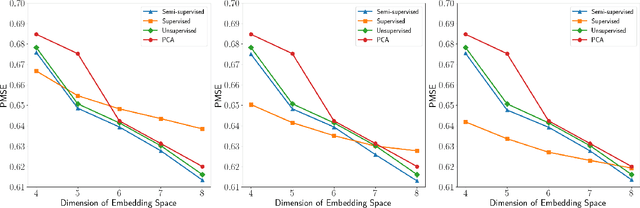
Identifying low-dimensional latent structures within high-dimensional data has long been a central topic in the machine learning community, driven by the need for data compression, storage, transmission, and deeper data understanding. Traditional methods, such as principal component analysis (PCA) and autoencoders (AE), operate in an unsupervised manner, ignoring label information even when it is available. In this work, we introduce a unified method capable of learning latent spaces in both unsupervised and supervised settings. We formulate the problem as a nonlinear multiple-response regression within an index model context. By applying the generalized Stein's lemma, the latent space can be estimated without knowing the nonlinear link functions. Our method can be viewed as a nonlinear generalization of PCA. Moreover, unlike AE and other neural network methods that operate as "black boxes", our approach not only offers better interpretability but also reduces computational complexity while providing strong theoretical guarantees. Comprehensive numerical experiments and real data analyses demonstrate the superior performance of our method.

Sparsity-Induced Global Matrix Autoregressive Model with Auxiliary Network Data

Jointly modeling and forecasting economic and financial variables across a large set of countries has long been a significant challenge. Two primary approaches have been utilized to address this issue: the vector autoregressive model with exogenous variables (VARX) and the matrix autoregression (MAR). The VARX model captures domestic dependencies, but treats variables exogenous to represent global factors driven by international trade. In contrast, the MAR model simultaneously considers variables from multiple countries but ignores the trade network. In this paper, we propose an extension of the MAR model that achieves these two aims at once, i.e., studying both international dependencies and the impact of the trade network on the global economy. Additionally, we introduce a sparse component to the model to differentiate between systematic and idiosyncratic cross-predictability. To estimate the model parameters, we propose both a likelihood estimation method and a bias-corrected alternating minimization version. We provide theoretical and empirical analyses of the model's properties, alongside presenting intriguing economic insights derived from our findings.

Time Series Generative Learning with Application to Brain Imaging Analysis

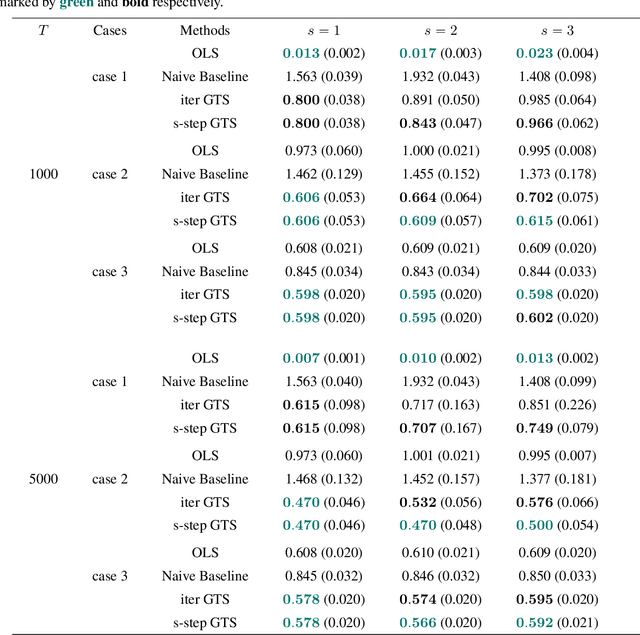
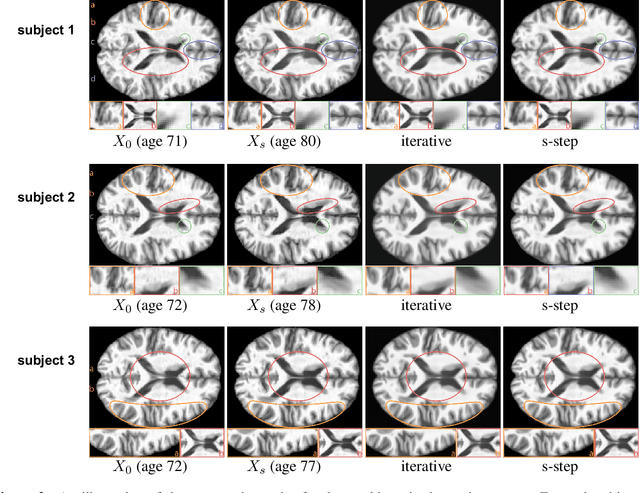
This paper focuses on the analysis of sequential image data, particularly brain imaging data such as MRI, fMRI, CT, with the motivation of understanding the brain aging process and neurodegenerative diseases. To achieve this goal, we investigate image generation in a time series context. Specifically, we formulate a min-max problem derived from the $f$-divergence between neighboring pairs to learn a time series generator in a nonparametric manner. The generator enables us to generate future images by transforming prior lag-k observations and a random vector from a reference distribution. With a deep neural network learned generator, we prove that the joint distribution of the generated sequence converges to the latent truth under a Markov and a conditional invariance condition. Furthermore, we extend our generation mechanism to a panel data scenario to accommodate multiple samples. The effectiveness of our mechanism is evaluated by generating real brain MRI sequences from the Alzheimer's Disease Neuroimaging Initiative. These generated image sequences can be used as data augmentation to enhance the performance of further downstream tasks, such as Alzheimer's disease detection.

Sparse Kronecker Product Decomposition: A General Framework of Signal Region Detection in Image Regression

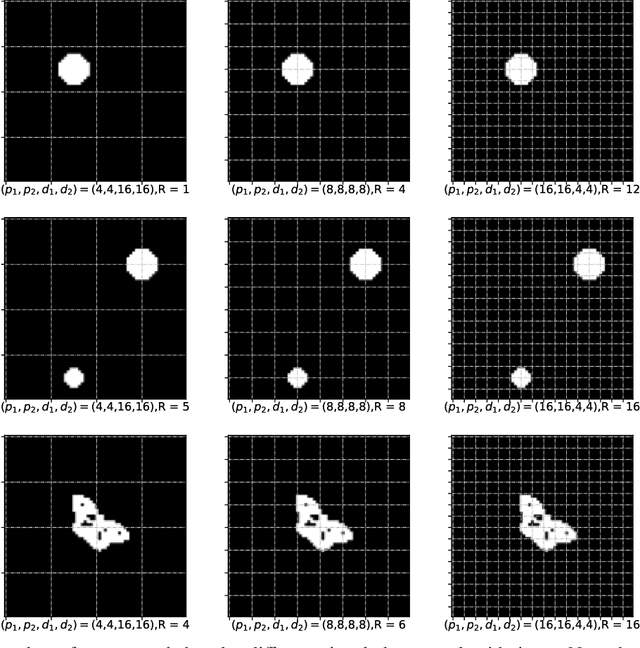
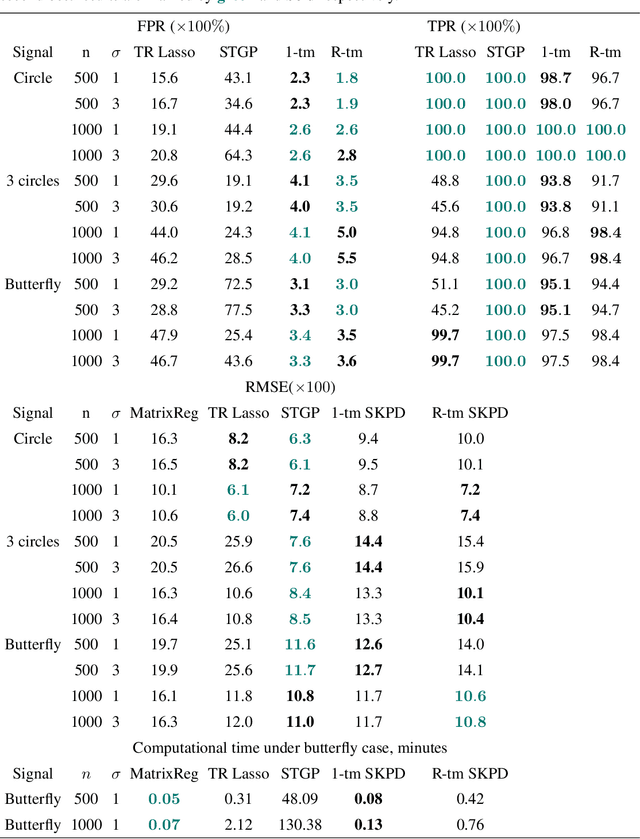
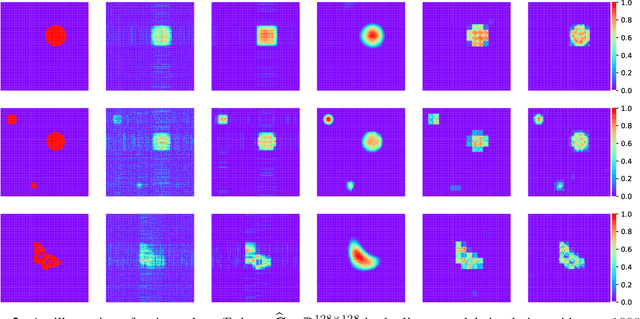
This paper aims to present the first Frequentist framework on signal region detection in high-resolution and high-order image regression problems. Image data and scalar-on-image regression are intensively studied in recent years. However, most existing studies on such topics focused on outcome prediction, while the research on image region detection is rather limited, even though the latter is often more important. In this paper, we develop a general framework named Sparse Kronecker Product Decomposition (SKPD) to tackle this issue. The SKPD framework is general in the sense that it works for both matrices (e.g., 2D grayscale images) and (high-order) tensors (e.g., 2D colored images, brain MRI/fMRI data) represented image data. Moreover, unlike many Bayesian approaches, our framework is computationally scalable for high-resolution image problems. Specifically, our framework includes: 1) the one-term SKPD; 2) the multi-term SKPD; and 3) the nonlinear SKPD. We propose nonconvex optimization problems to estimate the one-term and multi-term SKPDs and develop path-following algorithms for the nonconvex optimization. The computed solutions of the path-following algorithm are guaranteed to converge to the truth with a particularly chosen initialization even though the optimization is nonconvex. Moreover, the region detection consistency could also be guaranteed by the one-term and multi-term SKPD. The nonlinear SKPD is highly connected to shallow convolutional neural networks (CNN), particular to CNN with one convolutional layer and one fully connected layer. Effectiveness of SKPDs is validated by real brain imaging data in the UK Biobank database.

Metric learning by Similarity Network for Deep Semi-Supervised Learning

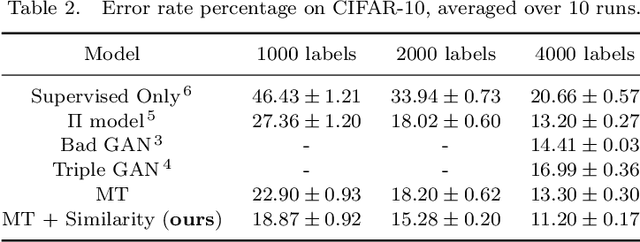
Deep semi-supervised learning has been widely implemented in the real-world due to the rapid development of deep learning. Recently, attention has shifted to the approaches such as Mean-Teacher to penalize the inconsistency between two perturbed input sets. Although these methods may achieve positive results, they ignore the relationship information between data instances. To solve this problem, we propose a novel method named Metric Learning by Similarity Network (MLSN), which aims to learn a distance metric adaptively on different domains. By co-training with the classification network, similarity network can learn more information about pairwise relationships and performs better on some empirical tasks than state-of-art methods.