Sparse Kronecker Product Decomposition: A General Framework of Signal Region Detection in Image Regression
Paper and Code
Oct 17, 2022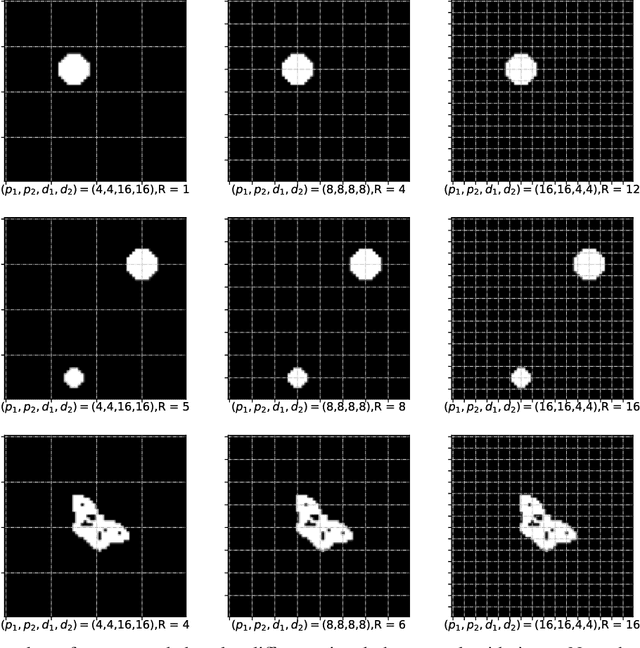
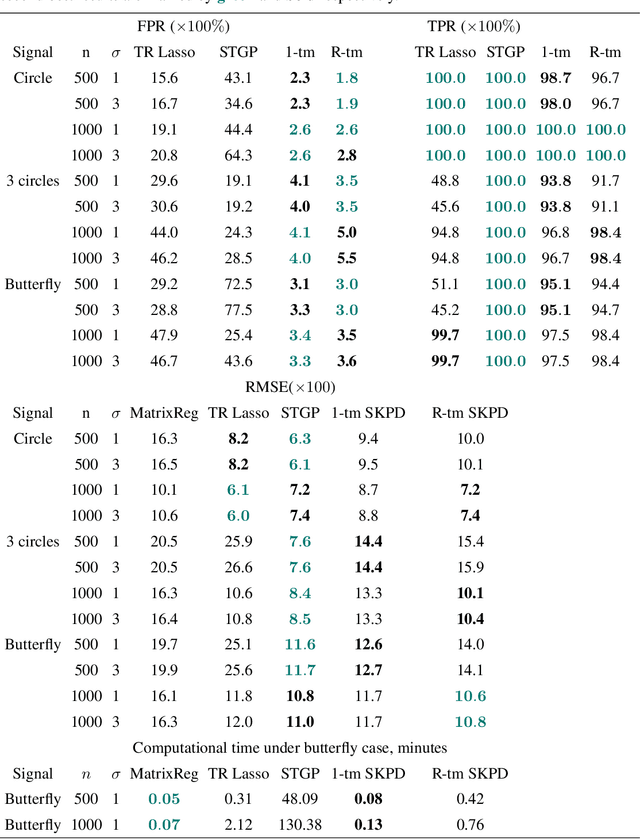
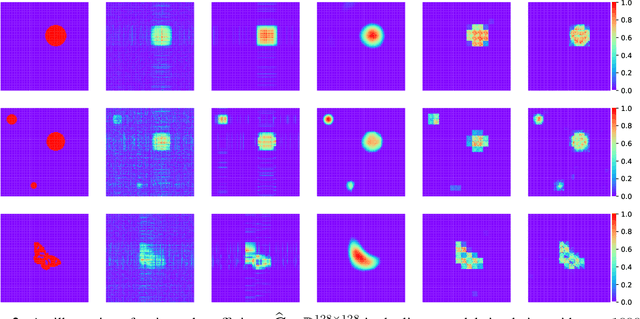

This paper aims to present the first Frequentist framework on signal region detection in high-resolution and high-order image regression problems. Image data and scalar-on-image regression are intensively studied in recent years. However, most existing studies on such topics focused on outcome prediction, while the research on image region detection is rather limited, even though the latter is often more important. In this paper, we develop a general framework named Sparse Kronecker Product Decomposition (SKPD) to tackle this issue. The SKPD framework is general in the sense that it works for both matrices (e.g., 2D grayscale images) and (high-order) tensors (e.g., 2D colored images, brain MRI/fMRI data) represented image data. Moreover, unlike many Bayesian approaches, our framework is computationally scalable for high-resolution image problems. Specifically, our framework includes: 1) the one-term SKPD; 2) the multi-term SKPD; and 3) the nonlinear SKPD. We propose nonconvex optimization problems to estimate the one-term and multi-term SKPDs and develop path-following algorithms for the nonconvex optimization. The computed solutions of the path-following algorithm are guaranteed to converge to the truth with a particularly chosen initialization even though the optimization is nonconvex. Moreover, the region detection consistency could also be guaranteed by the one-term and multi-term SKPD. The nonlinear SKPD is highly connected to shallow convolutional neural networks (CNN), particular to CNN with one convolutional layer and one fully connected layer. Effectiveness of SKPDs is validated by real brain imaging data in the UK Biobank database.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge