Near-Optimal High-Probability Convergence for Non-Convex Stochastic Optimization with Variance Reduction

Traditional analyses for non-convex stochastic optimization problems characterize convergence bounds in expectation, which is inadequate as it does not supply a useful performance guarantee on a single run. Motivated by its importance, an emerging line of literature has recently studied the high-probability convergence behavior of several algorithms, including the classic stochastic gradient descent (SGD). However, no high-probability results are established for optimization algorithms with variance reduction, which is known to accelerate the convergence process and has been the de facto algorithmic technique for stochastic optimization at large. To close this important gap, we introduce a new variance-reduced algorithm for non-convex stochastic optimization, which we call Generalized SignSTORM. We show that with probability at least $1-\delta$, our algorithm converges at the rate of $O(\log(dT/\delta)/T^{1/3})$ after $T$ iterations where $d$ is the problem dimension. This convergence guarantee matches the existing lower bound up to a log factor, and to our best knowledge, is the first high-probability minimax (near-)optimal result. Finally, we demonstrate the effectiveness of our algorithm through numerical experiments.

A Model-based Projection Technique for Segmenting Customers

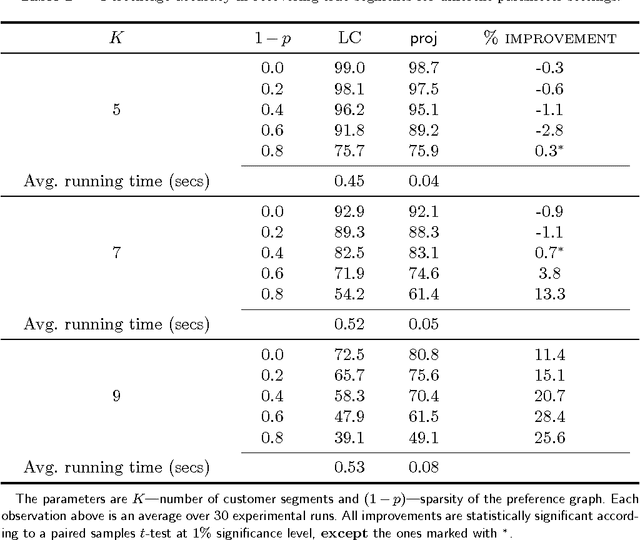
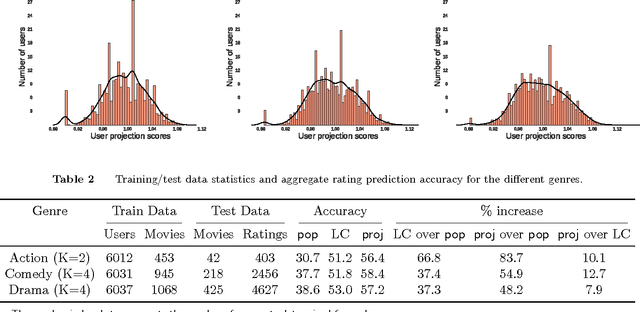
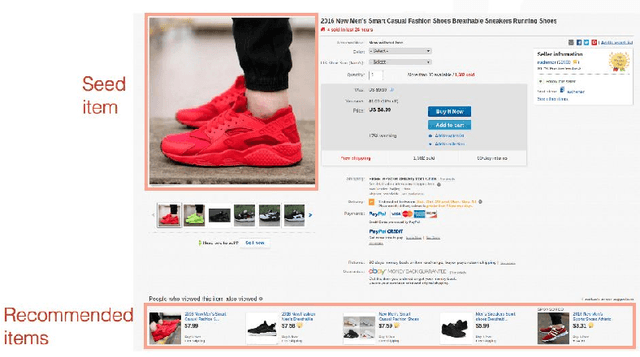
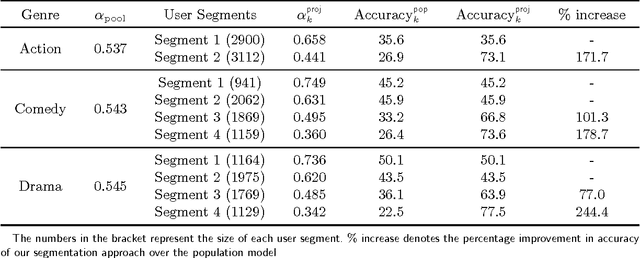
We consider the problem of segmenting a large population of customers into non-overlapping groups with similar preferences, using diverse preference observations such as purchases, ratings, clicks, etc. over subsets of items. We focus on the setting where the universe of items is large (ranging from thousands to millions) and unstructured (lacking well-defined attributes) and each customer provides observations for only a few items. These data characteristics limit the applicability of existing techniques in marketing and machine learning. To overcome these limitations, we propose a model-based projection technique, which transforms the diverse set of observations into a more comparable scale and deals with missing data by projecting the transformed data onto a low-dimensional space. We then cluster the projected data to obtain the customer segments. Theoretically, we derive precise necessary and sufficient conditions that guarantee asymptotic recovery of the true customer segments. Empirically, we demonstrate the speed and performance of our method in two real-world case studies: (a) 84% improvement in the accuracy of new movie recommendations on the MovieLens data set and (b) 6% improvement in the performance of similar item recommendations algorithm on an offline dataset at eBay. We show that our method outperforms standard latent-class and demographic-based techniques.

Sparse Choice Models

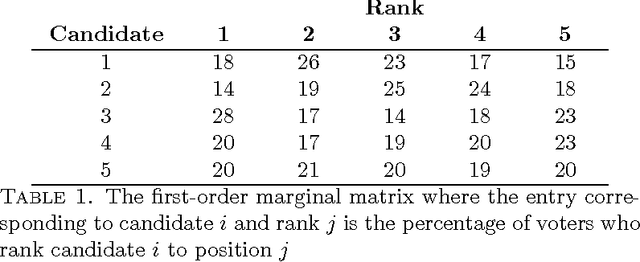
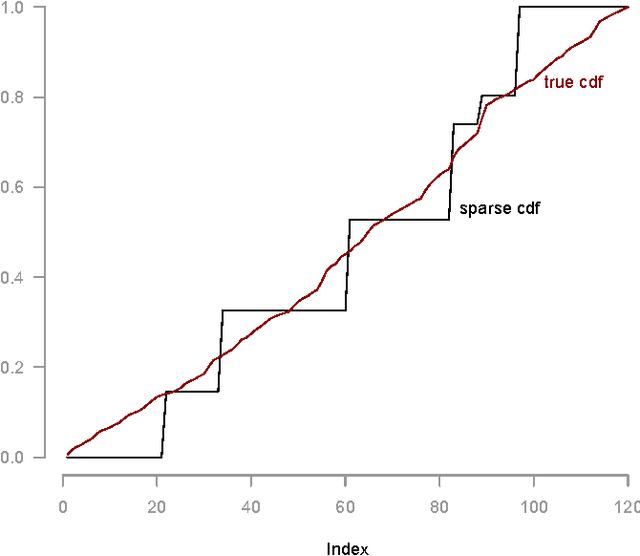
Choice models, which capture popular preferences over objects of interest, play a key role in making decisions whose eventual outcome is impacted by human choice behavior. In most scenarios, the choice model, which can effectively be viewed as a distribution over permutations, must be learned from observed data. The observed data, in turn, may frequently be viewed as (partial, noisy) information about marginals of this distribution over permutations. As such, the search for an appropriate choice model boils down to learning a distribution over permutations that is (near-)consistent with observed information about this distribution. In this work, we pursue a non-parametric approach which seeks to learn a choice model (i.e. a distribution over permutations) with {\em sparsest} possible support, and consistent with observed data. We assume that the data observed consists of noisy information pertaining to the marginals of the choice model we seek to learn. We establish that {\em any} choice model admits a `very' sparse approximation in the sense that there exists a choice model whose support is small relative to the dimension of the observed data and whose marginals approximately agree with the observed marginal information. We further show that under, what we dub, `signature' conditions, such a sparse approximation can be found in a computationally efficiently fashion relative to a brute force approach. An empirical study using the American Psychological Association election data-set suggests that our approach manages to unearth useful structural properties of the underlying choice model using the sparse approximation found. Our results further suggest that the signature condition is a potential alternative to the recently popularized Restricted Null Space condition for efficient recovery of sparse models.