Fast Genetic Algorithms
Paper and Code
Mar 15, 2017
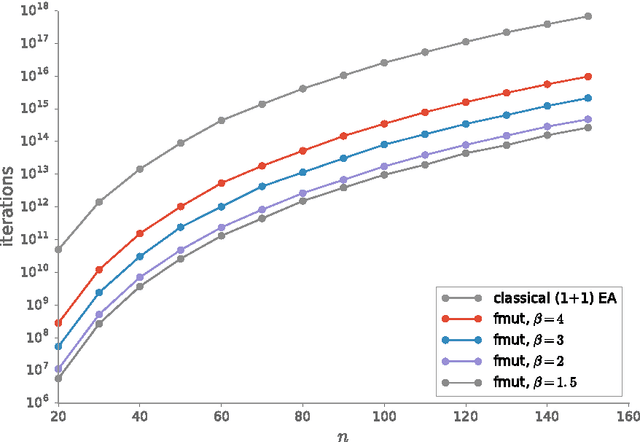
For genetic algorithms using a bit-string representation of length~$n$, the general recommendation is to take $1/n$ as mutation rate. In this work, we discuss whether this is really justified for multimodal functions. Taking jump functions and the $(1+1)$ evolutionary algorithm as the simplest example, we observe that larger mutation rates give significantly better runtimes. For the $\jump_{m,n}$ function, any mutation rate between $2/n$ and $m/n$ leads to a speed-up at least exponential in $m$ compared to the standard choice. The asymptotically best runtime, obtained from using the mutation rate $m/n$ and leading to a speed-up super-exponential in $m$, is very sensitive to small changes of the mutation rate. Any deviation by a small $(1 \pm \eps)$ factor leads to a slow-down exponential in $m$. Consequently, any fixed mutation rate gives strongly sub-optimal results for most jump functions. Building on this observation, we propose to use a random mutation rate $\alpha/n$, where $\alpha$ is chosen from a power-law distribution. We prove that the $(1+1)$ EA with this heavy-tailed mutation rate optimizes any $\jump_{m,n}$ function in a time that is only a small polynomial (in~$m$) factor above the one stemming from the optimal rate for this $m$. Our heavy-tailed mutation operator yields similar speed-ups (over the best known performance guarantees) for the vertex cover problem in bipartite graphs and the matching problem in general graphs. Following the example of fast simulated annealing, fast evolution strategies, and fast evolutionary programming, we propose to call genetic algorithms using a heavy-tailed mutation operator \emph{fast genetic algorithms}.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge