Safe Deployment of Offline Reinforcement Learning via Input Convex Action Correction

Offline reinforcement learning (offline RL) offers a promising framework for developing control strategies in chemical process systems using historical data, without the risks or costs of online experimentation. This work investigates the application of offline RL to the safe and efficient control of an exothermic polymerisation continuous stirred-tank reactor. We introduce a Gymnasium-compatible simulation environment that captures the reactor's nonlinear dynamics, including reaction kinetics, energy balances, and operational constraints. The environment supports three industrially relevant scenarios: startup, grade change down, and grade change up. It also includes reproducible offline datasets generated from proportional-integral controllers with randomised tunings, providing a benchmark for evaluating offline RL algorithms in realistic process control tasks. We assess behaviour cloning and implicit Q-learning as baseline algorithms, highlighting the challenges offline agents face, including steady-state offsets and degraded performance near setpoints. To address these issues, we propose a novel deployment-time safety layer that performs gradient-based action correction using input convex neural networks (PICNNs) as learned cost models. The PICNN enables real-time, differentiable correction of policy actions by descending a convex, state-conditioned cost surface, without requiring retraining or environment interaction. Experimental results show that offline RL, particularly when combined with convex action correction, can outperform traditional control approaches and maintain stability across all scenarios. These findings demonstrate the feasibility of integrating offline RL with interpretable and safety-aware corrections for high-stakes chemical process control, and lay the groundwork for more reliable data-driven automation in industrial systems.

Deep Learning Surrogates for Real-Time Gas Emission Inversion

Real-time identification and quantification of greenhouse-gas emissions under transient atmospheric conditions is a critical challenge in environmental monitoring. We introduce a spatio-temporal inversion framework that embeds a deep-learning surrogate of computational fluid dynamics (CFD) within a sequential Monte Carlo algorithm to perform Bayesian inference of both emission rate and source location in dynamic flow fields. By substituting costly numerical solvers with a multilayer perceptron trained on high-fidelity CFD outputs, our surrogate captures spatial heterogeneity and temporal evolution of gas dispersion, while delivering near-real-time predictions. Validation on the Chilbolton methane release dataset demonstrates comparable accuracy to full CFD solvers and Gaussian plume models, yet achieves orders-of-magnitude faster runtimes. Further experiments under simulated obstructed-flow scenarios confirm robustness in complex environments. This work reconciles physical fidelity with computational feasibility, offering a scalable solution for industrial emissions monitoring and other time-sensitive spatio-temporal inversion tasks in environmental and scientific modeling.

Developing, Analyzing, and Evaluating Vehicular Lane Keeping Algorithms Under Dynamic Lighting and Weather Conditions Using Electric Vehicles

Self-driving vehicles have the potential to reduce accidents and fatalities on the road. Many production vehicles already come equipped with basic self-driving capabilities, but have trouble following lanes in adverse lighting and weather conditions. Therefore, we develop, analyze, and evaluate two vehicular lane-keeping algorithms under dynamic weather conditions using a combined deep learning- and hand-crafted approach and an end-to-end deep learning approach. We use image segmentation- and linear-regression based deep learning to drive the vehicle toward the center of the lane, measuring the amount of laps completed, average speed, and average steering error per lap. Our hybrid model completes more laps than our end-to-end deep learning model. In the future, we are interested in combining our algorithms to form one cohesive approach to lane-following.

Conformal Predictions Enhanced Expert-guided Meshing with Graph Neural Networks

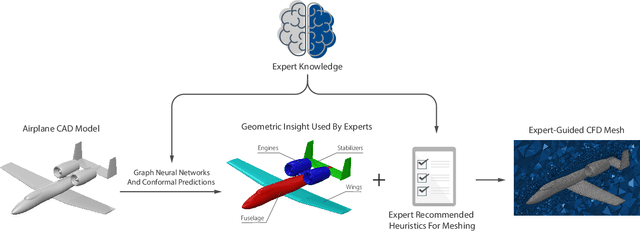
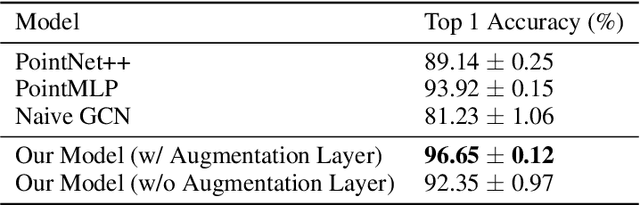
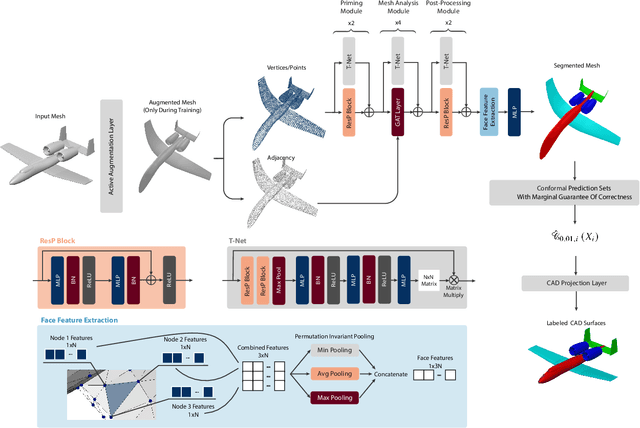
Computational Fluid Dynamics (CFD) is widely used in different engineering fields, but accurate simulations are dependent upon proper meshing of the simulation domain. While highly refined meshes may ensure precision, they come with high computational costs. Similarly, adaptive remeshing techniques require multiple simulations and come at a great computational cost. This means that the meshing process is reliant upon expert knowledge and years of experience. Automating mesh generation can save significant time and effort and lead to a faster and more efficient design process. This paper presents a machine learning-based scheme that utilizes Graph Neural Networks (GNN) and expert guidance to automatically generate CFD meshes for aircraft models. In this work, we introduce a new 3D segmentation algorithm that outperforms two state-of-the-art models, PointNet++ and PointMLP, for surface classification. We also present a novel approach to project predictions from 3D mesh segmentation models to CAD surfaces using the conformal predictions method, which provides marginal statistical guarantees and robust uncertainty quantification and handling. We demonstrate that the addition of conformal predictions effectively enables the model to avoid under-refinement, hence failure, in CFD meshing even for weak and less accurate models. Finally, we demonstrate the efficacy of our approach through a real-world case study that demonstrates that our automatically generated mesh is comparable in quality to expert-generated meshes and enables the solver to converge and produce accurate results. Furthermore, we compare our approach to the alternative of adaptive remeshing in the same case study and find that our method is 5 times faster in the overall process of simulation. The code and data for this project are made publicly available at https://github.com/ahnobari/AutoSurf.

Automated Code generation for Information Technology Tasks in YAML through Large Language Models

The recent improvement in code generation capabilities due to the use of large language models has mainly benefited general purpose programming languages. Domain specific languages, such as the ones used for IT Automation, have received far less attention, despite involving many active developers and being an essential component of modern cloud platforms. This work focuses on the generation of Ansible-YAML, a widely used markup language for IT Automation. We present Ansible Wisdom, a natural-language to Ansible-YAML code generation tool, aimed at improving IT automation productivity. Ansible Wisdom is a transformer-based model, extended by training with a new dataset containing Ansible-YAML. We also develop two novel performance metrics for YAML and Ansible to capture the specific characteristics of this domain. Results show that Ansible Wisdom can accurately generate Ansible script from natural language prompts with performance comparable or better than existing state of the art code generation models.

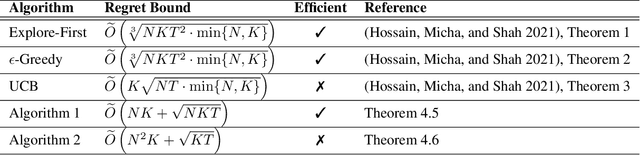
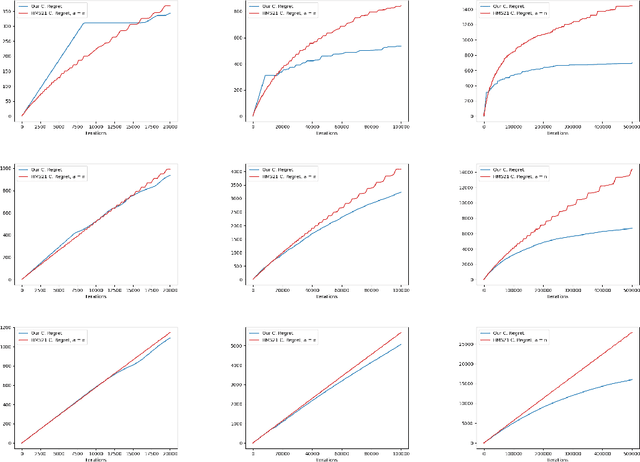
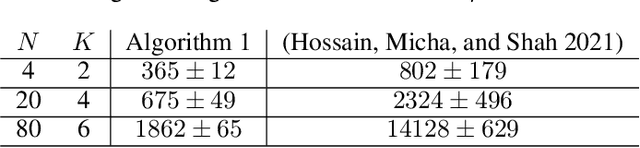
An Efficient Algorithm for Fair Multi-Agent Multi-Armed Bandit with Low Regret

Recently a multi-agent variant of the classical multi-armed bandit was proposed to tackle fairness issues in online learning. Inspired by a long line of work in social choice and economics, the goal is to optimize the Nash social welfare instead of the total utility. Unfortunately previous algorithms either are not efficient or achieve sub-optimal regret in terms of the number of rounds $T$. We propose a new efficient algorithm with lower regret than even previous inefficient ones. For $N$ agents, $K$ arms, and $T$ rounds, our approach has a regret bound of $\tilde{O}(\sqrt{NKT} + NK)$. This is an improvement to the previous approach, which has regret bound of $\tilde{O}( \min(NK, \sqrt{N} K^{3/2})\sqrt{T})$. We also complement our efficient algorithm with an inefficient approach with $\tilde{O}(\sqrt{KT} + N^2K)$ regret. The experimental findings confirm the effectiveness of our efficient algorithm compared to the previous approaches.

Locally Private $k$-Means Clustering with Constant Multiplicative Approximation and Near-Optimal Additive Error

Given a data set of size $n$ in $d'$-dimensional Euclidean space, the $k$-means problem asks for a set of $k$ points (called centers) so that the sum of the $\ell_2^2$-distances between points of a given data set of size $n$ and the set of $k$ centers is minimized. Recent work on this problem in the locally private setting achieves constant multiplicative approximation with additive error $\tilde{O} (n^{1/2 + a} \cdot k \cdot \max \{\sqrt{d}, \sqrt{k} \})$ and proves a lower bound of $\Omega(\sqrt{n})$ on the additive error for any solution with a constant number of rounds. In this work we bridge the gap between the exponents of $n$ in the upper and lower bounds on the additive error with two new algorithms. Given any $\alpha>0$, our first algorithm achieves a multiplicative approximation guarantee which is at most a $(1+\alpha)$ factor greater than that of any non-private $k$-means clustering algorithm with $k^{\tilde{O}(1/\alpha^2)} \sqrt{d' n} \mbox{poly}\log n$ additive error. Given any $c>\sqrt{2}$, our second algorithm achieves $O(k^{1 + \tilde{O}(1/(2c^2-1))} \sqrt{d' n} \mbox{poly} \log n)$ additive error with constant multiplicative approximation. Both algorithms go beyond the $\Omega(n^{1/2 + a})$ factor that occurs in the additive error for arbitrarily small parameters $a$ in previous work, and the second algorithm in particular shows for the first time that it is possible to solve the locally private $k$-means problem in a constant number of rounds with constant factor multiplicative approximation and polynomial dependence on $k$ in the additive error arbitrarily close to linear.

Differentially Private Clustering via Maximum Coverage

This paper studies the problem of clustering in metric spaces while preserving the privacy of individual data. Specifically, we examine differentially private variants of the k-medians and Euclidean k-means problems. We present polynomial algorithms with constant multiplicative error and lower additive error than the previous state-of-the-art for each problem. Additionally, our algorithms use a clustering algorithm without differential privacy as a black-box. This allows practitioners to control the trade-off between runtime and approximation factor by choosing a suitable clustering algorithm to use.