Improved Learning-augmented Algorithms for k-means and k-medians Clustering

We consider the problem of clustering in the learning-augmented setting, where we are given a data set in $d$-dimensional Euclidean space, and a label for each data point given by an oracle indicating what subsets of points should be clustered together. This setting captures situations where we have access to some auxiliary information about the data set relevant for our clustering objective, for instance the labels output by a neural network. Following prior work, we assume that there are at most an $\alpha \in (0,c)$ for some $c<1$ fraction of false positives and false negatives in each predicted cluster, in the absence of which the labels would attain the optimal clustering cost $\mathrm{OPT}$. For a dataset of size $m$, we propose a deterministic $k$-means algorithm that produces centers with improved bound on clustering cost compared to the previous randomized algorithm while preserving the $O( d m \log m)$ runtime. Furthermore, our algorithm works even when the predictions are not very accurate, i.e. our bound holds for $\alpha$ up to $1/2$, an improvement over $\alpha$ being at most $1/7$ in the previous work. For the $k$-medians problem we improve upon prior work by achieving a biquadratic improvement in the dependence of the approximation factor on the accuracy parameter $\alpha$ to get a cost of $(1+O(\alpha))\mathrm{OPT}$, while requiring essentially just $O(md \log^3 m/\alpha)$ runtime.

Streaming Submodular Maximization with Differential Privacy

In this work, we study the problem of privately maximizing a submodular function in the streaming setting. Extensive work has been done on privately maximizing submodular functions in the general case when the function depends upon the private data of individuals. However, when the size of the data stream drawn from the domain of the objective function is large or arrives very fast, one must privately optimize the objective within the constraints of the streaming setting. We establish fundamental differentially private baselines for this problem and then derive better trade-offs between privacy and utility for the special case of decomposable submodular functions. A submodular function is decomposable when it can be written as a sum of submodular functions; this structure arises naturally when each summand function models the utility of an individual and the goal is to study the total utility of the whole population as in the well-known Combinatorial Public Projects Problem. Finally, we complement our theoretical analysis with experimental corroboration.

Locally Private $k$-Means Clustering with Constant Multiplicative Approximation and Near-Optimal Additive Error

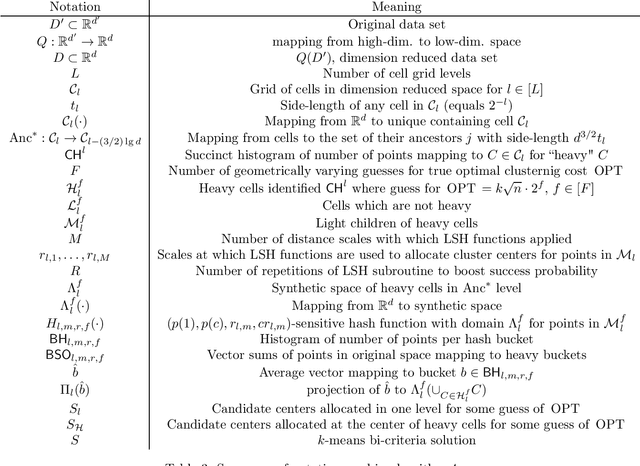
Given a data set of size $n$ in $d'$-dimensional Euclidean space, the $k$-means problem asks for a set of $k$ points (called centers) so that the sum of the $\ell_2^2$-distances between points of a given data set of size $n$ and the set of $k$ centers is minimized. Recent work on this problem in the locally private setting achieves constant multiplicative approximation with additive error $\tilde{O} (n^{1/2 + a} \cdot k \cdot \max \{\sqrt{d}, \sqrt{k} \})$ and proves a lower bound of $\Omega(\sqrt{n})$ on the additive error for any solution with a constant number of rounds. In this work we bridge the gap between the exponents of $n$ in the upper and lower bounds on the additive error with two new algorithms. Given any $\alpha>0$, our first algorithm achieves a multiplicative approximation guarantee which is at most a $(1+\alpha)$ factor greater than that of any non-private $k$-means clustering algorithm with $k^{\tilde{O}(1/\alpha^2)} \sqrt{d' n} \mbox{poly}\log n$ additive error. Given any $c>\sqrt{2}$, our second algorithm achieves $O(k^{1 + \tilde{O}(1/(2c^2-1))} \sqrt{d' n} \mbox{poly} \log n)$ additive error with constant multiplicative approximation. Both algorithms go beyond the $\Omega(n^{1/2 + a})$ factor that occurs in the additive error for arbitrarily small parameters $a$ in previous work, and the second algorithm in particular shows for the first time that it is possible to solve the locally private $k$-means problem in a constant number of rounds with constant factor multiplicative approximation and polynomial dependence on $k$ in the additive error arbitrarily close to linear.

Differentially private $k$-means clustering via exponential mechanism and max cover

We introduce a new $(\epsilon_p, \delta_p)$-differentially private algorithm for the $k$-means clustering problem. Given a dataset in Euclidean space, the $k$-means clustering problem requires one to find $k$ points in that space such that the sum of squares of Euclidean distances between each data point and its closest respective point among the $k$ returned is minimised. Although there exist privacy-preserving methods with good theoretical guarantees to solve this problem [Balcan et al., 2017; Kaplan and Stemmer, 2018], in practice it is seen that it is the additive error which dictates the practical performance of these methods. By reducing the problem to a sequence of instances of maximum coverage on a grid, we are able to derive a new method that achieves lower additive error then previous works. For input datasets with cardinality $n$ and diameter $\Delta$, our algorithm has an $O(\Delta^2 (k \log^2 n \log(1/\delta_p)/\epsilon_p + k\sqrt{d \log(1/\delta_p)}/\epsilon_p))$ additive error whilst maintaining constant multiplicative error. We conclude with some experiments and find an improvement over previously implemented work for this problem.

Differentially Private Decomposable Submodular Maximization

We study the problem of differentially private constrained maximization of decomposable submodular functions. A submodular function is decomposable if it takes the form of a sum of submodular functions. The special case of maximizing a monotone, decomposable submodular function under cardinality constraints is known as the Combinatorial Public Projects (CPP) problem [Papadimitriou et al., 2008]. Previous work by Gupta et al. [2010] gave a differentially private algorithm for the CPP problem. We extend this work by designing differentially private algorithms for both monotone and non-monotone decomposable submodular maximization under general matroid constraints, with competitive utility guarantees. We complement our theoretical bounds with experiments demonstrating empirical performance, which improves over the differentially private algorithms for the general case of submodular maximization and is close to the performance of non-private algorithms.

Learning Gaussian Graphical Models via Multiplicative Weights

Graphical model selection in Markov random fields is a fundamental problem in statistics and machine learning. Two particularly prominent models, the Ising model and Gaussian model, have largely developed in parallel using different (though often related) techniques, and several practical algorithms with rigorous sample complexity bounds have been established for each. In this paper, we adapt a recently proposed algorithm of Klivans and Meka (FOCS, 2017), based on the method of multiplicative weight updates, from the Ising model to the Gaussian model, via non-trivial modifications to both the algorithm and its analysis. The algorithm enjoys a sample complexity bound that is qualitatively similar to others in the literature, has a low runtime $O(mp^2)$ in the case of $m$ samples and $p$ nodes, and can trivially be implemented in an online manner.