Private Frequency Estimation via Projective Geometry
Paper and Code
Mar 01, 2022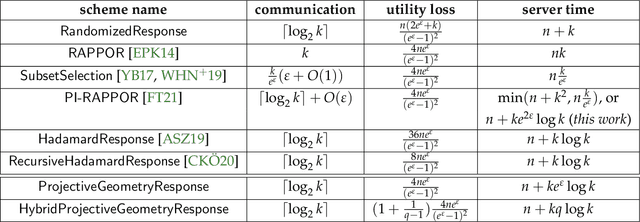
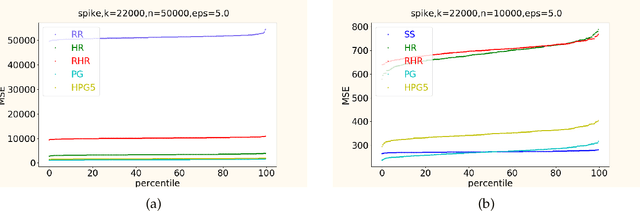
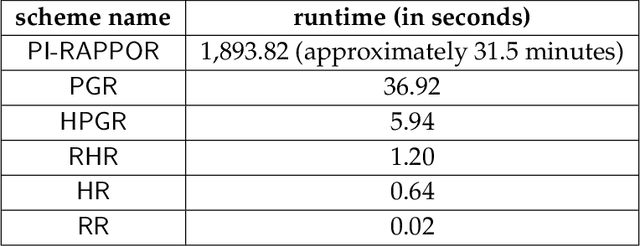
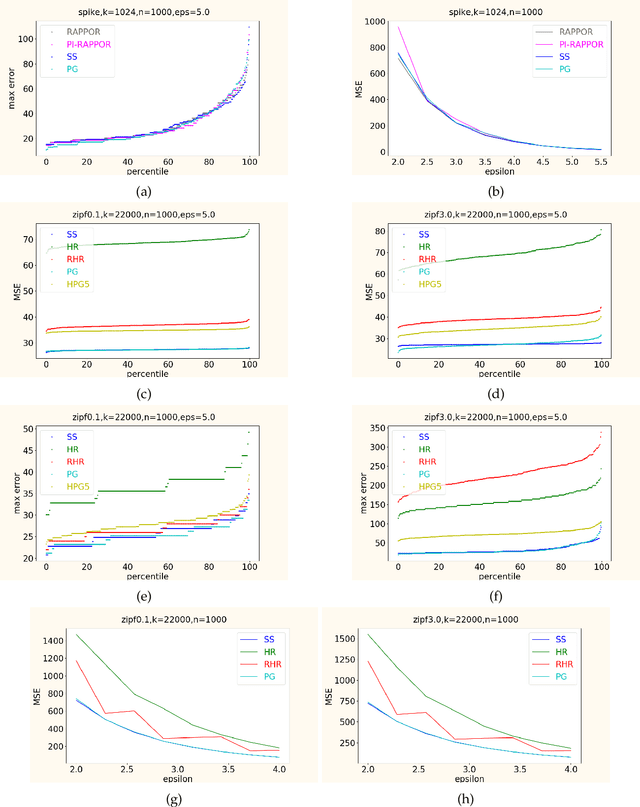
In this work, we propose a new algorithm ProjectiveGeometryResponse (PGR) for locally differentially private (LDP) frequency estimation. For a universe size of $k$ and with $n$ users, our $\varepsilon$-LDP algorithm has communication cost $\lceil\log_2k\rceil$ bits in the private coin setting and $\varepsilon\log_2 e + O(1)$ in the public coin setting, and has computation cost $O(n + k\exp(\varepsilon) \log k)$ for the server to approximately reconstruct the frequency histogram, while achieving the state-of-the-art privacy-utility tradeoff. In many parameter settings used in practice this is a significant improvement over the $ O(n+k^2)$ computation cost that is achieved by the recent PI-RAPPOR algorithm (Feldman and Talwar; 2021). Our empirical evaluation shows a speedup of over 50x over PI-RAPPOR while using approximately 75x less memory for practically relevant parameter settings. In addition, the running time of our algorithm is within an order of magnitude of HadamardResponse (Acharya, Sun, and Zhang; 2019) and RecursiveHadamardResponse (Chen, Kairouz, and Ozgur; 2020) which have significantly worse reconstruction error. The error of our algorithm essentially matches that of the communication- and time-inefficient but utility-optimal SubsetSelection (SS) algorithm (Ye and Barg; 2017). Our new algorithm is based on using Projective Planes over a finite field to define a small collection of sets that are close to being pairwise independent and a dynamic programming algorithm for approximate histogram reconstruction on the server side. We also give an extension of PGR, which we call HybridProjectiveGeometryResponse, that allows trading off computation time with utility smoothly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge