Improved Space Bounds for Learning with Experts
Paper and Code
Mar 02, 2023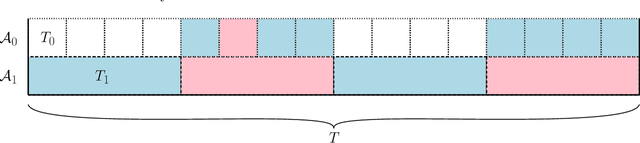
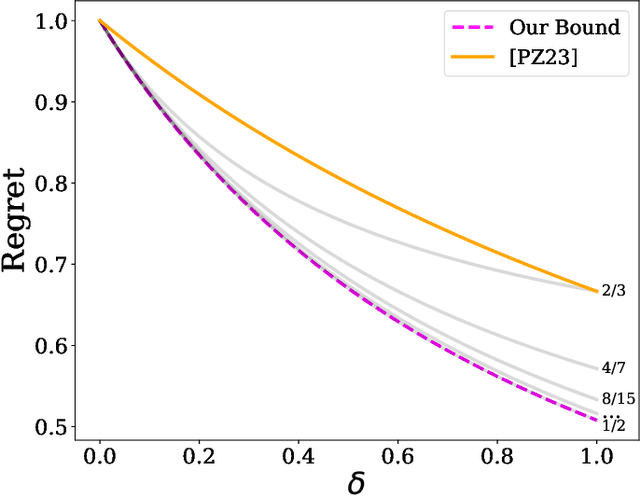
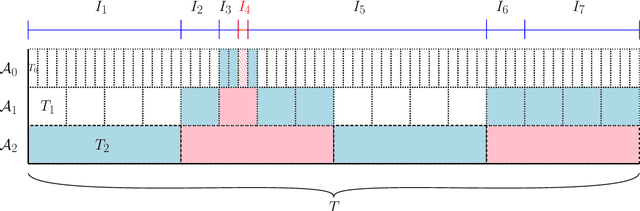
We give improved tradeoffs between space and regret for the online learning with expert advice problem over $T$ days with $n$ experts. Given a space budget of $n^{\delta}$ for $\delta \in (0,1)$, we provide an algorithm achieving regret $\tilde{O}(n^2 T^{1/(1+\delta)})$, improving upon the regret bound $\tilde{O}(n^2 T^{2/(2+\delta)})$ in the recent work of [PZ23]. The improvement is particularly salient in the regime $\delta \rightarrow 1$ where the regret of our algorithm approaches $\tilde{O}_n(\sqrt{T})$, matching the $T$ dependence in the standard online setting without space restrictions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge