Large Language Models: An Applied Econometric Framework

Large language models (LLMs) are being used in economics research to form predictions, label text, simulate human responses, generate hypotheses, and even produce data for times and places where such data don't exist. While these uses are creative, are they valid? When can we abstract away from the inner workings of an LLM and simply rely on their outputs? We develop an econometric framework to answer this question. Our framework distinguishes between two types of empirical tasks. Using LLM outputs for prediction problems (including hypothesis generation) is valid under one condition: no "leakage" between the LLM's training dataset and the researcher's sample. Using LLM outputs for estimation problems to automate the measurement of some economic concept (expressed by some text or from human subjects) requires an additional assumption: LLM outputs must be as good as the gold standard measurements they replace. Otherwise estimates can be biased, even if LLM outputs are highly accurate but not perfectly so. We document the extent to which these conditions are violated and the implications for research findings in illustrative applications to finance and political economy. We also provide guidance to empirical researchers. The only way to ensure no training leakage is to use open-source LLMs with documented training data and published weights. The only way to deal with LLM measurement error is to collect validation data and model the error structure. A corollary is that if such conditions can't be met for a candidate LLM application, our strong advice is: don't.

Program Evaluation with Remotely Sensed Outcomes

While traditional program evaluations typically rely on surveys to measure outcomes, certain economic outcomes such as living standards or environmental quality may be infeasible or costly to collect. As a result, recent empirical work estimates treatment effects using remotely sensed variables (RSVs), such mobile phone activity or satellite images, instead of ground-truth outcome measurements. Common practice predicts the economic outcome from the RSV, using an auxiliary sample of labeled RSVs, and then uses such predictions as the outcome in the experiment. We prove that this approach leads to biased estimates of treatment effects when the RSV is a post-outcome variable. We nonparametrically identify the treatment effect, using an assumption that reflects the logic of recent empirical research: the conditional distribution of the RSV remains stable across both samples, given the outcome and treatment. Our results do not require researchers to know or consistently estimate the relationship between the RSV, outcome, and treatment, which is typically mis-specified with unstructured data. We form a representation of the RSV for downstream causal inference by predicting the outcome and predicting the treatment, with better predictions leading to more precise causal estimates. We re-evaluate the efficacy of a large-scale public program in India, showing that the program's measured effects on local consumption and poverty can be replicated using satellite

Evaluating the World Model Implicit in a Generative Model

Recent work suggests that large language models may implicitly learn world models. How should we assess this possibility? We formalize this question for the case where the underlying reality is governed by a deterministic finite automaton. This includes problems as diverse as simple logical reasoning, geographic navigation, game-playing, and chemistry. We propose new evaluation metrics for world model recovery inspired by the classic Myhill-Nerode theorem from language theory. We illustrate their utility in three domains: game playing, logic puzzles, and navigation. In all domains, the generative models we consider do well on existing diagnostics for assessing world models, but our evaluation metrics reveal their world models to be far less coherent than they appear. Such incoherence creates fragility: using a generative model to solve related but subtly different tasks can lead it to fail badly. Building generative models that meaningfully capture the underlying logic of the domains they model would be immensely valuable; our results suggest new ways to assess how close a given model is to that goal.

Do Large Language Models Perform the Way People Expect? Measuring the Human Generalization Function

What makes large language models (LLMs) impressive is also what makes them hard to evaluate: their diversity of uses. To evaluate these models, we must understand the purposes they will be used for. We consider a setting where these deployment decisions are made by people, and in particular, people's beliefs about where an LLM will perform well. We model such beliefs as the consequence of a human generalization function: having seen what an LLM gets right or wrong, people generalize to where else it might succeed. We collect a dataset of 19K examples of how humans make generalizations across 79 tasks from the MMLU and BIG-Bench benchmarks. We show that the human generalization function can be predicted using NLP methods: people have consistent structured ways to generalize. We then evaluate LLM alignment with the human generalization function. Our results show that -- especially for cases where the cost of mistakes is high -- more capable models (e.g. GPT-4) can do worse on the instances people choose to use them for, exactly because they are not aligned with the human generalization function.

Counterfactual Risk Assessments under Unmeasured Confounding

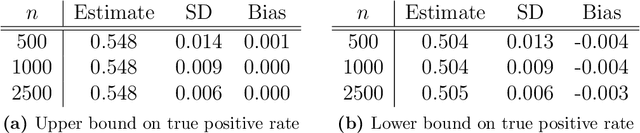
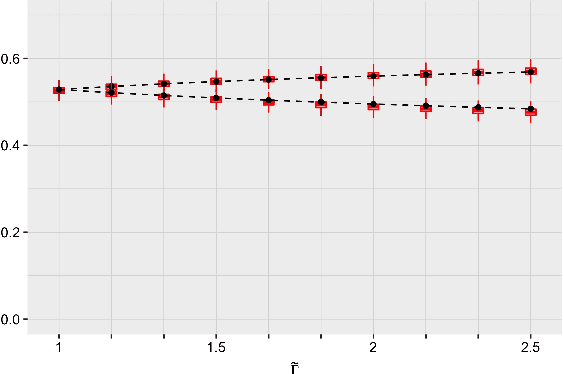
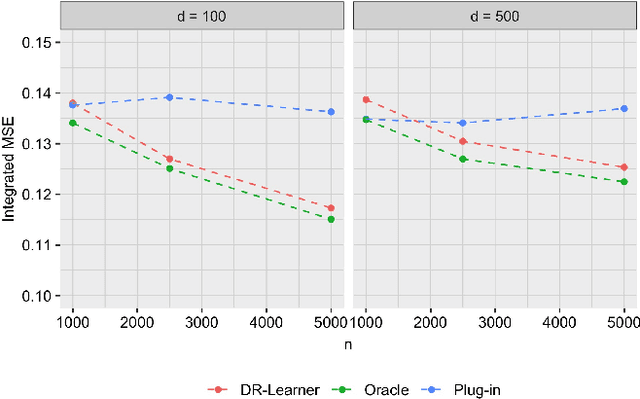
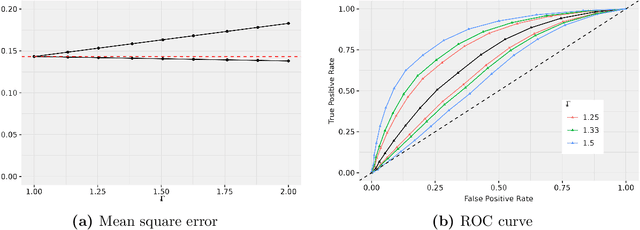
Statistical risk assessments inform consequential decisions such as pretrial release in criminal justice, and loan approvals in consumer finance. Such risk assessments make counterfactual predictions, predicting the likelihood of an outcome under a proposed decision (e.g., what would happen if we approved this loan?). A central challenge, however, is that there may have been unmeasured confounders that jointly affected past decisions and outcomes in the historical data. This paper proposes a tractable mean outcome sensitivity model that bounds the extent to which unmeasured confounders could affect outcomes on average. The mean outcome sensitivity model partially identifies the conditional likelihood of the outcome under the proposed decision, popular predictive performance metrics (e.g., accuracy, calibration, TPR, FPR), and commonly-used predictive disparities. We derive their sharp identified sets, and we then solve three tasks that are essential to deploying statistical risk assessments in high-stakes settings. First, we propose a doubly-robust learning procedure for the bounds on the conditional likelihood of the outcome under the proposed decision. Second, we translate our estimated bounds on the conditional likelihood of the outcome under the proposed decision into a robust, plug-in decision-making policy. Third, we develop doubly-robust estimators of the bounds on the predictive performance of an existing risk assessment.

Characterizing Fairness Over the Set of Good Models Under Selective Labels

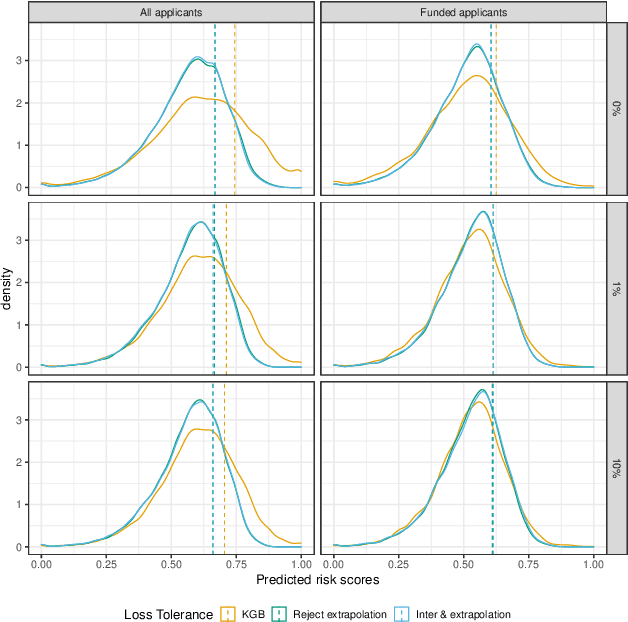
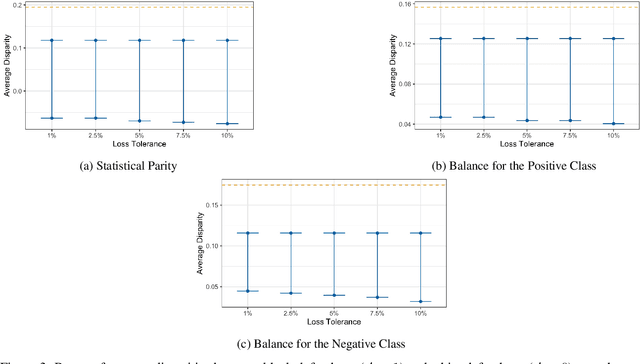
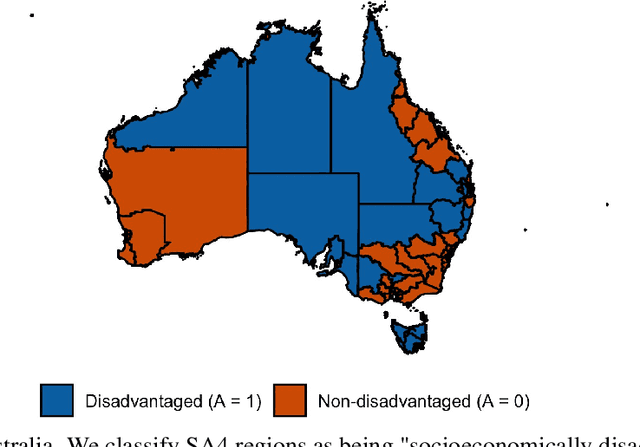
Algorithmic risk assessments are increasingly used to make and inform decisions in a wide variety of high-stakes settings. In practice, there is often a multitude of predictive models that deliver similar overall performance, an empirical phenomenon commonly known as the "Rashomon Effect." While many competing models may perform similarly overall, they may have different properties over various subgroups, and therefore have drastically different predictive fairness properties. In this paper, we develop a framework for characterizing predictive fairness properties over the set of models that deliver similar overall performance, or "the set of good models." We provide tractable algorithms to compute the range of attainable group-level predictive disparities and the disparity minimizing model over the set of good models. We extend our framework to address the empirically relevant challenge of selectively labelled data in the setting where the selection decision and outcome are unconfounded given the observed data features. We illustrate our methods in two empirical applications. In a real world credit-scoring task, we build a model with lower predictive disparities than the benchmark model, and demonstrate the benefits of properly accounting for the selective labels problem. In a recidivism risk prediction task, we audit an existing risk score, and find that it generates larger predictive disparities than any model in the set of good models.

Bias In, Bias Out? Evaluating the Folk Wisdom

We evaluate the folk wisdom that algorithms trained on data produced by biased human decision-makers necessarily reflect this bias. We consider a setting where training labels are only generated if a biased decision-maker takes a particular action, and so bias arises due to selection into the training data. In our baseline model, the more biased the decision-maker is toward a group, the more the algorithm favors that group. We refer to this phenomenon as "algorithmic affirmative action." We then clarify the conditions that give rise to algorithmic affirmative action. Whether a prediction algorithm reverses or inherits bias depends critically on how the decision-maker affects the training data as well as the label used in training. We illustrate our main theoretical results in a simulation study applied to the New York City Stop, Question and Frisk dataset.