Dependent Randomized Rounding for Budget Constrained Experimental Design

Policymakers in resource-constrained settings require experimental designs that satisfy strict budget limits while ensuring precise estimation of treatment effects. We propose a framework that applies a dependent randomized rounding procedure to convert assignment probabilities into binary treatment decisions. Our proposed solution preserves the marginal treatment probabilities while inducing negative correlations among assignments, leading to improved estimator precision through variance reduction. We establish theoretical guarantees for the inverse propensity weighted and general linear estimators, and demonstrate through empirical studies that our approach yields efficient and accurate inference under fixed budget constraints.

Counterfactual Risk Assessments under Unmeasured Confounding

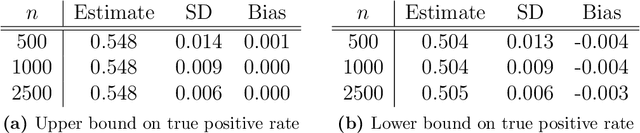
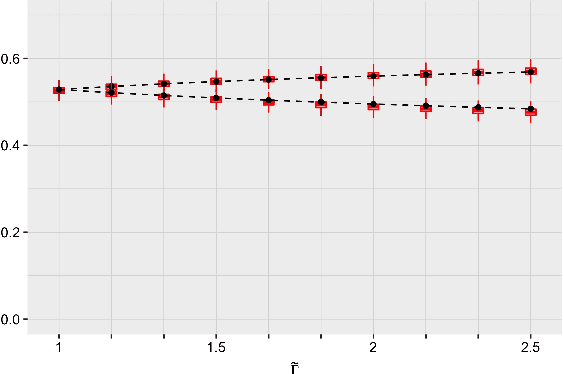
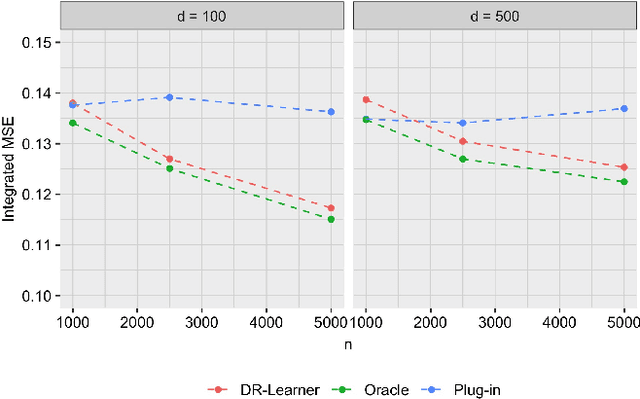
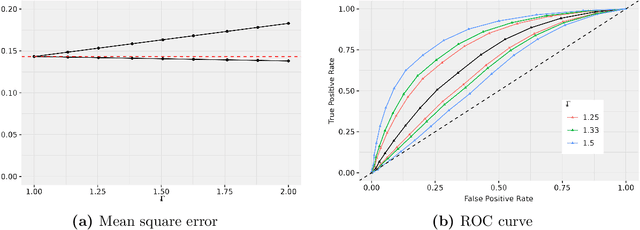
Statistical risk assessments inform consequential decisions such as pretrial release in criminal justice, and loan approvals in consumer finance. Such risk assessments make counterfactual predictions, predicting the likelihood of an outcome under a proposed decision (e.g., what would happen if we approved this loan?). A central challenge, however, is that there may have been unmeasured confounders that jointly affected past decisions and outcomes in the historical data. This paper proposes a tractable mean outcome sensitivity model that bounds the extent to which unmeasured confounders could affect outcomes on average. The mean outcome sensitivity model partially identifies the conditional likelihood of the outcome under the proposed decision, popular predictive performance metrics (e.g., accuracy, calibration, TPR, FPR), and commonly-used predictive disparities. We derive their sharp identified sets, and we then solve three tasks that are essential to deploying statistical risk assessments in high-stakes settings. First, we propose a doubly-robust learning procedure for the bounds on the conditional likelihood of the outcome under the proposed decision. Second, we translate our estimated bounds on the conditional likelihood of the outcome under the proposed decision into a robust, plug-in decision-making policy. Third, we develop doubly-robust estimators of the bounds on the predictive performance of an existing risk assessment.

FADE: FAir Double Ensemble Learning for Observable and Counterfactual Outcomes

Methods for building fair predictors often involve tradeoffs between fairness and accuracy and between different fairness criteria, but the nature of these tradeoffs varies. Recent work seeks to characterize these tradeoffs in specific problem settings, but these methods often do not accommodate users who wish to improve the fairness of an existing benchmark model without sacrificing accuracy, or vice versa. These results are also typically restricted to observable accuracy and fairness criteria. We develop a flexible framework for fair ensemble learning that allows users to efficiently explore the fairness-accuracy space or to improve the fairness or accuracy of a benchmark model. Our framework can simultaneously target multiple observable or counterfactual fairness criteria, and it enables users to combine a large number of previously trained and newly trained predictors. We provide theoretical guarantees that our estimators converge at fast rates. We apply our method on both simulated and real data, with respect to both observable and counterfactual accuracy and fairness criteria. We show that, surprisingly, multiple unfairness measures can sometimes be minimized simultaneously with little impact on accuracy, relative to unconstrained predictors or existing benchmark models.