Program Evaluation with Remotely Sensed Outcomes

While traditional program evaluations typically rely on surveys to measure outcomes, certain economic outcomes such as living standards or environmental quality may be infeasible or costly to collect. As a result, recent empirical work estimates treatment effects using remotely sensed variables (RSVs), such mobile phone activity or satellite images, instead of ground-truth outcome measurements. Common practice predicts the economic outcome from the RSV, using an auxiliary sample of labeled RSVs, and then uses such predictions as the outcome in the experiment. We prove that this approach leads to biased estimates of treatment effects when the RSV is a post-outcome variable. We nonparametrically identify the treatment effect, using an assumption that reflects the logic of recent empirical research: the conditional distribution of the RSV remains stable across both samples, given the outcome and treatment. Our results do not require researchers to know or consistently estimate the relationship between the RSV, outcome, and treatment, which is typically mis-specified with unstructured data. We form a representation of the RSV for downstream causal inference by predicting the outcome and predicting the treatment, with better predictions leading to more precise causal estimates. We re-evaluate the efficacy of a large-scale public program in India, showing that the program's measured effects on local consumption and poverty can be replicated using satellite

Dynamic covariate balancing: estimating treatment effects over time

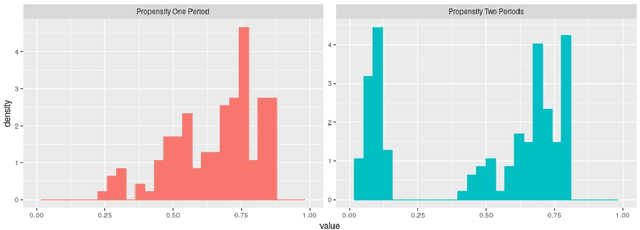
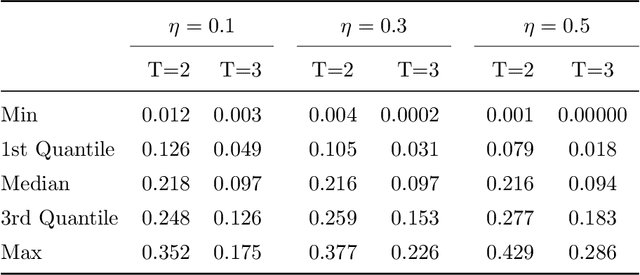
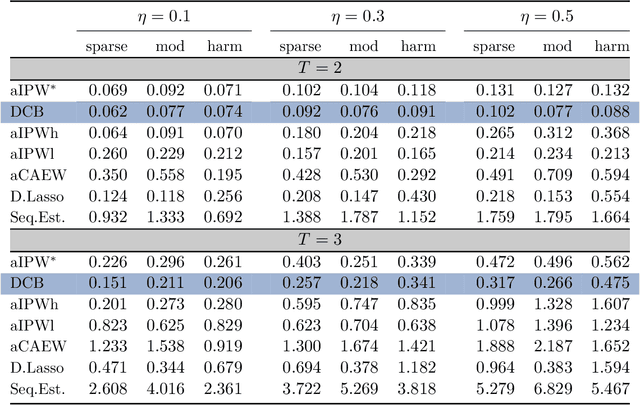
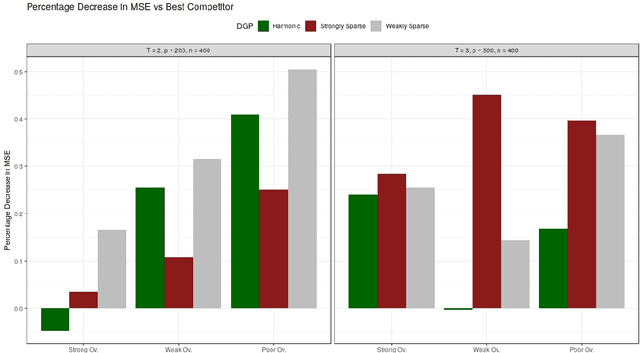
This paper discusses the problem of estimation and inference on time-varying treatments. We propose a method for inference on treatment histories, by introducing a \textit{dynamic} covariate balancing method. Our approach allows for (i) treatments to propagate arbitrarily over time; (ii) non-stationarity and heterogeneity of treatment effects; (iii) high-dimensional covariates, and (iv) unknown propensity score functions. We study the asymptotic properties of the estimator, and we showcase the parametric convergence rate of the proposed procedure. We illustrate in simulations and an empirical application the advantage of the method over state-of-the-art competitors.

Policy choice in experiments with unknown interference

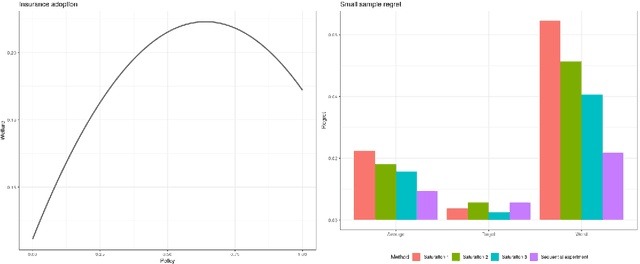
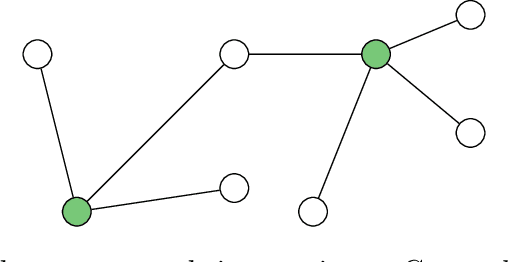
This paper discusses experimental design for inference and estimation of individualized treatment allocation rules in the presence of unknown interference, with units being organized into large independent clusters. The contribution is two-fold. First, we design a short pilot study with few clusters for testing whether base-line interventions are welfare-maximizing, with its rejection motivating larger-scale experimentation. Second, we introduce an adaptive randomization procedure to estimate welfare-maximizing individual treatment allocation rules valid under unobserved interference. We propose non-parametric estimators of direct treatments and marginal spillover effects, which serve for hypothesis testing and policy-design. We discuss the asymptotic properties of the estimators and small sample regret guarantees of the estimated policy. Finally, we illustrate the method's advantage in simulations calibrated to an existing experiment on information diffusion.

Fair Policy Targeting

One of the major concerns of targeting interventions on individuals in social welfare programs is discrimination: individualized treatments may induce disparities on sensitive attributes such as age, gender, or race. This paper addresses the question of the design of fair and efficient treatment allocation rules. We adopt the non-maleficence perspective of "first do no harm": we propose to select the fairest allocation within the Pareto frontier. We provide envy-freeness justifications to novel counterfactual notions of fairness. We discuss easy-to-implement estimators of the policy function, by casting the optimization into a mixed-integer linear program formulation. We derive regret bounds on the unfairness of the estimated policy function, and small sample guarantees on the Pareto frontier. Finally, we illustrate our method using an application from education economics.

Policy Targeting under Network Interference

The empirical analysis of experiments and quasi-experiments often seeks to determine the optimal allocation of treatments that maximizes social welfare. In the presence of interference, spillover effects lead to a new formulation of the statistical treatment choice problem. This paper develops a novel method to construct individual-specific optimal treatment allocation rules under network interference. Several features make the proposed methodology particularly appealing for applications: we construct targeting rules that depend on an arbitrary set of individual, neighbors' and network characteristics, and we allow for general constraints on the policy function; we consider heterogeneous direct and spillover effects, arbitrary, possibly non-linear, regression models, and we propose estimators that are robust to model misspecification; the method flexibly accommodates for cases where researchers only observe local information of the network. From a theoretical perspective, we establish the first set of guarantees on the utilitarian regret under interference, and we show that it achieves the min-max optimal rate in scenarios of practical and theoretical interest. We discuss the empirical performance in simulations and we illustrate our method by investigating the role of social networks in micro-finance decisions.

Synthetic learner: model-free inference on treatments over time

Understanding of the effect of a particular treatment or a policy pertains to many areas of interest -- ranging from political economics, marketing to health-care and personalized treatment studies. In this paper, we develop a non-parametric, model-free test for detecting the effects of treatment over time that extends widely used Synthetic Control tests. The test is built on counterfactual predictions arising from many learning algorithms. In the Neyman-Rubin potential outcome framework with possible carry-over effects, we show that the proposed test is asymptotically consistent for stationary, beta mixing processes. We do not assume that class of learners captures the correct model necessarily. We also discuss estimates of the average treatment effect, and we provide regret bounds on the predictive performance. To the best of our knowledge, this is the first set of results that allow for example any Random Forest to be useful for provably valid statistical inference in the Synthetic Control setting. In experiments, we show that our Synthetic Learner is substantially more powerful than classical methods based on Synthetic Control or Difference-in-Differences, especially in the presence of non-linear outcome models.