Dynamic covariate balancing: estimating treatment effects over time
Paper and Code
Mar 01, 2021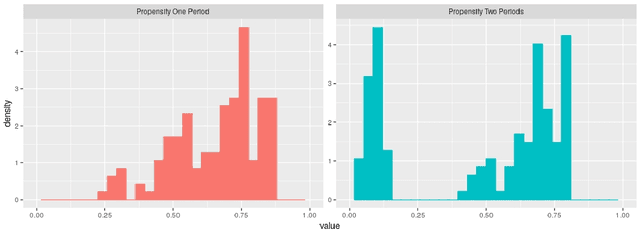
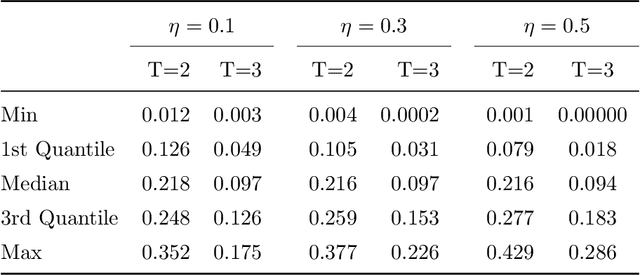
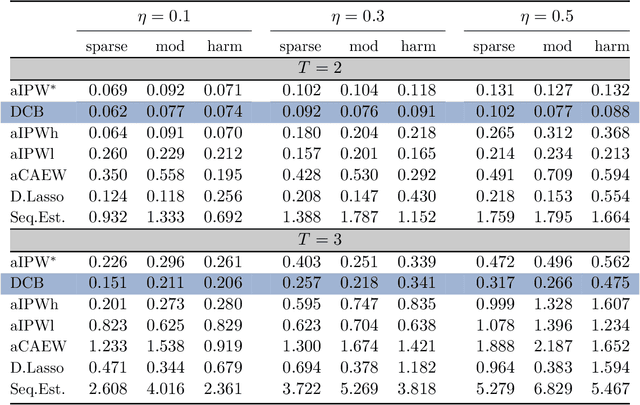
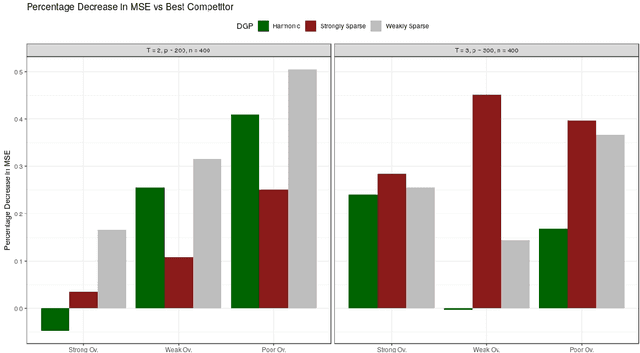
This paper discusses the problem of estimation and inference on time-varying treatments. We propose a method for inference on treatment histories, by introducing a \textit{dynamic} covariate balancing method. Our approach allows for (i) treatments to propagate arbitrarily over time; (ii) non-stationarity and heterogeneity of treatment effects; (iii) high-dimensional covariates, and (iv) unknown propensity score functions. We study the asymptotic properties of the estimator, and we showcase the parametric convergence rate of the proposed procedure. We illustrate in simulations and an empirical application the advantage of the method over state-of-the-art competitors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge