Keep on Swimming: Real Attackers Only Need Partial Knowledge of a Multi-Model System

Recent approaches in machine learning often solve a task using a composition of multiple models or agentic architectures. When targeting a composed system with adversarial attacks, it might not be computationally or informationally feasible to train an end-to-end proxy model or a proxy model for every component of the system. We introduce a method to craft an adversarial attack against the overall multi-model system when we only have a proxy model for the final black-box model, and when the transformation applied by the initial models can make the adversarial perturbations ineffective. Current methods handle this by applying many copies of the first model/transformation to an input and then re-use a standard adversarial attack by averaging gradients, or learning a proxy model for both stages. To our knowledge, this is the first attack specifically designed for this threat model and our method has a substantially higher attack success rate (80% vs 25%) and contains 9.4% smaller perturbations (MSE) compared to prior state-of-the-art methods. Our experiments focus on a supervised image pipeline, but we are confident the attack will generalize to other multi-model settings [e.g. a mix of open/closed source foundation models], or agentic systems

Fairness, Accuracy, and Unreliable Data

This thesis investigates three areas targeted at improving the reliability of machine learning; fairness in machine learning, strategic classification, and algorithmic robustness. Each of these domains has special properties or structure that can complicate learning. A theme throughout this thesis is thinking about ways in which a `plain' empirical risk minimization algorithm will be misleading or ineffective because of a mis-match between classical learning theory assumptions and specific properties of some data distribution in the wild. Theoretical understanding in eachof these domains can help guide best practices and allow for the design of effective, reliable, and robust systems.

Investigating the Semantic Robustness of CLIP-based Zero-Shot Anomaly Segmentation

Zero-shot anomaly segmentation using pre-trained foundation models is a promising approach that enables effective algorithms without expensive, domain-specific training or fine-tuning. Ensuring that these methods work across various environmental conditions and are robust to distribution shifts is an open problem. We investigate the performance of WinCLIP [14] zero-shot anomaly segmentation algorithm by perturbing test data using three semantic transformations: bounded angular rotations, bounded saturation shifts, and hue shifts. We empirically measure a lower performance bound by aggregating across per-sample worst-case perturbations and find that average performance drops by up to 20% in area under the ROC curve and 40% in area under the per-region overlap curve. We find that performance is consistently lowered on three CLIP backbones, regardless of model architecture or learning objective, demonstrating a need for careful performance evaluation.

Bayesian Strategic Classification

In strategic classification, agents modify their features, at a cost, to ideally obtain a positive classification from the learner's classifier. The typical response of the learner is to carefully modify their classifier to be robust to such strategic behavior. When reasoning about agent manipulations, most papers that study strategic classification rely on the following strong assumption: agents fully know the exact parameters of the deployed classifier by the learner. This often is an unrealistic assumption when using complex or proprietary machine learning techniques in real-world prediction tasks. We initiate the study of partial information release by the learner in strategic classification. We move away from the traditional assumption that agents have full knowledge of the classifier. Instead, we consider agents that have a common distributional prior on which classifier the learner is using. The learner in our model can reveal truthful, yet not necessarily complete, information about the deployed classifier to the agents. The learner's goal is to release just enough information about the classifier to maximize accuracy. We show how such partial information release can, counter-intuitively, benefit the learner's accuracy, despite increasing agents' abilities to manipulate. We show that while it is intractable to compute the best response of an agent in the general case, there exist oracle-efficient algorithms that can solve the best response of the agents when the learner's hypothesis class is the class of linear classifiers, or when the agents' cost function satisfies a natural notion of submodularity as we define. We then turn our attention to the learner's optimization problem and provide both positive and negative results on the algorithmic problem of how much information the learner should release about the classifier to maximize their expected accuracy.

On the Vulnerability of Fairness Constrained Learning to Malicious Noise

We consider the vulnerability of fairness-constrained learning to small amounts of malicious noise in the training data. Konstantinov and Lampert (2021) initiated the study of this question and presented negative results showing there exist data distributions where for several fairness constraints, any proper learner will exhibit high vulnerability when group sizes are imbalanced. Here, we present a more optimistic view, showing that if we allow randomized classifiers, then the landscape is much more nuanced. For example, for Demographic Parity we show we can incur only a $\Theta(\alpha)$ loss in accuracy, where $\alpha$ is the malicious noise rate, matching the best possible even without fairness constraints. For Equal Opportunity, we show we can incur an $O(\sqrt{\alpha})$ loss, and give a matching $\Omega(\sqrt{\alpha})$lower bound. In contrast, Konstantinov and Lampert (2021) showed for proper learners the loss in accuracy for both notions is $\Omega(1)$. The key technical novelty of our work is how randomization can bypass simple "tricks" an adversary can use to amplify his power. We also consider additional fairness notions including Equalized Odds and Calibration. For these fairness notions, the excess accuracy clusters into three natural regimes $O(\alpha)$,$O(\sqrt{\alpha})$ and $O(1)$. These results provide a more fine-grained view of the sensitivity of fairness-constrained learning to adversarial noise in training data.

Certifiable (Multi)Robustness Against Patch Attacks Using ERM

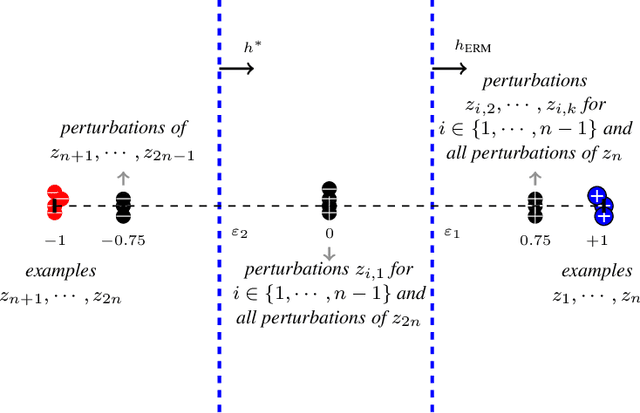
Consider patch attacks, where at test-time an adversary manipulates a test image with a patch in order to induce a targeted misclassification. We consider a recent defense to patch attacks, Patch-Cleanser (Xiang et al. [2022]). The Patch-Cleanser algorithm requires a prediction model to have a ``two-mask correctness'' property, meaning that the prediction model should correctly classify any image when any two blank masks replace portions of the image. Xiang et al. learn a prediction model to be robust to two-mask operations by augmenting the training set with pairs of masks at random locations of training images and performing empirical risk minimization (ERM) on the augmented dataset. However, in the non-realizable setting when no predictor is perfectly correct on all two-mask operations on all images, we exhibit an example where ERM fails. To overcome this challenge, we propose a different algorithm that provably learns a predictor robust to all two-mask operations using an ERM oracle, based on prior work by Feige et al. [2015]. We also extend this result to a multiple-group setting, where we can learn a predictor that achieves low robust loss on all groups simultaneously.

Sequential Strategic Screening

We initiate the study of strategic behavior in screening processes with multiple classifiers. We focus on two contrasting settings: a conjunctive setting in which an individual must satisfy all classifiers simultaneously, and a sequential setting in which an individual to succeed must satisfy classifiers one at a time. In other words, we introduce the combination of strategic classification with screening processes. We show that sequential screening pipelines exhibit new and surprising behavior where individuals can exploit the sequential ordering of the tests to zig-zag between classifiers without having to simultaneously satisfy all of them. We demonstrate an individual can obtain a positive outcome using a limited manipulation budget even when far from the intersection of the positive regions of every classifier. Finally, we consider a learner whose goal is to design a sequential screening process that is robust to such manipulations, and provide a construction for the learner that optimizes a natural objective.

Multi Stage Screening: Enforcing Fairness and Maximizing Efficiency in a Pre-Existing Pipeline

Consider an actor making selection decisions using a series of classifiers, which we term a sequential screening process. The early stages filter out some applicants, and in the final stage an expensive but accurate test is applied to the individuals that make it to the final stage. Since the final stage is expensive, if there are multiple groups with different fractions of positives at the penultimate stage (even if a slight gap), then the firm may naturally only choose to the apply the final (interview) stage solely to the highest precision group which would be clearly unfair to the other groups. Even if the firm is required to interview all of those who pass the final round, the tests themselves could have the property that qualified individuals from some groups pass more easily than qualified individuals from others. Thus, we consider requiring Equality of Opportunity (qualified individuals from each each group have the same chance of reaching the final stage and being interviewed). We then examine the goal of maximizing quantities of interest to the decision maker subject to this constraint, via modification of the probabilities of promotion through the screening process at each stage based on performance at the previous stage. We exhibit algorithms for satisfying Equal Opportunity over the selection process and maximizing precision (the fraction of interview that yield qualified candidates) as well as linear combinations of precision and recall (recall determines the number of applicants needed per hire) at the end of the final stage. We also present examples showing that the solution space is non-convex, which motivate our exact and (FPTAS) approximation algorithms for maximizing the linear combination of precision and recall. Finally, we discuss the `price of' adding additional restrictions, such as not allowing the decision maker to use group membership in its decision process.

Recovering from Biased Data: Can Fairness Constraints Improve Accuracy?

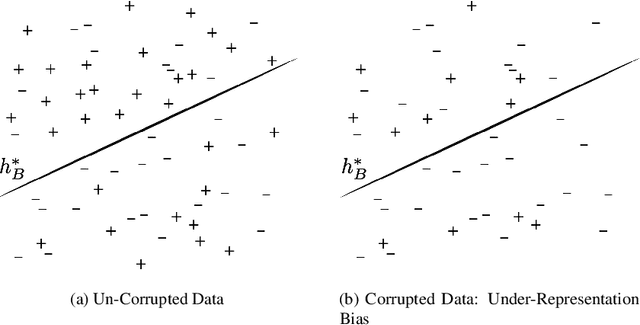
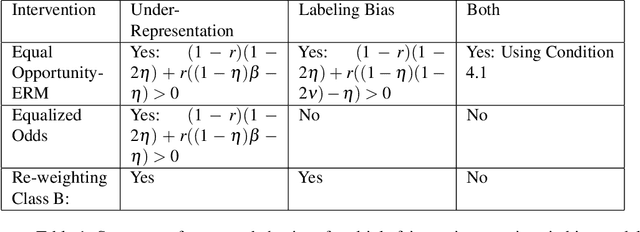
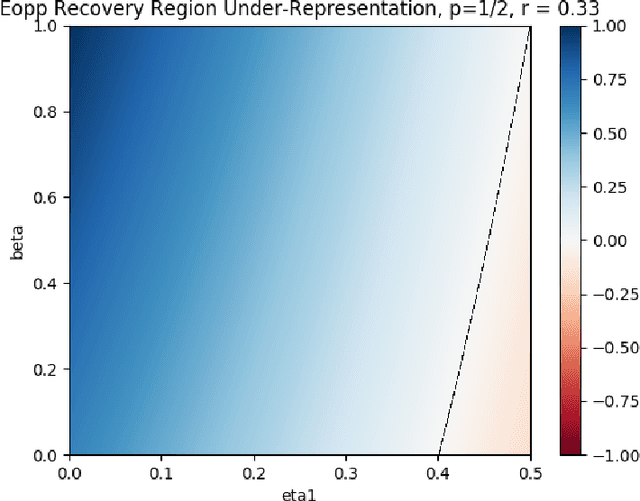
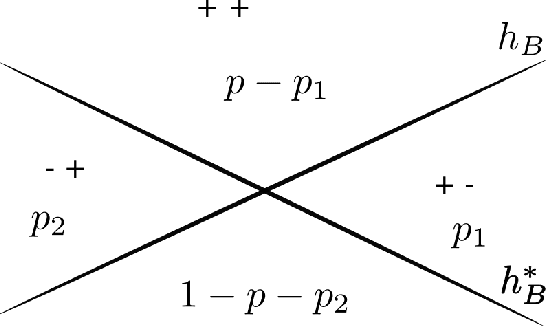
Multiple fairness constraints have been proposed in the literature, motivated by a range of concerns about how demographic groups might be treated unfairly by machine learning classifiers. In this work we consider a different motivation; learning from biased training data. We posit several ways in which training data may be biased, including having a more noisy or negatively biased labeling process on members of a disadvantaged group, or a decreased prevalence of positive or negative examples from the disadvantaged group, or both. Given such biased training data, Empirical Risk Minimization (ERM) may produce a classifier that not only is biased but also has suboptimal accuracy on the true data distribution. We examine the ability of fairness-constrained ERM to correct this problem. In particular, we find that the Equal Opportunity fairness constraint (Hardt, Price, and Srebro 2016) combined with ERM will provably recover the Bayes Optimal Classifier under a range of bias models. We also consider other recovery methods including reweighting the training data, Equalized Odds, and Demographic Parity. These theoretical results provide additional motivation for considering fairness interventions even if an actor cares primarily about accuracy.