Learning-Based Algorithms for Graph Searching Problems

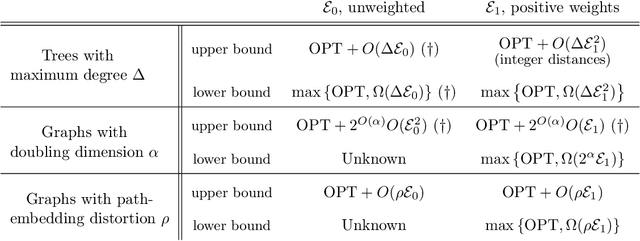
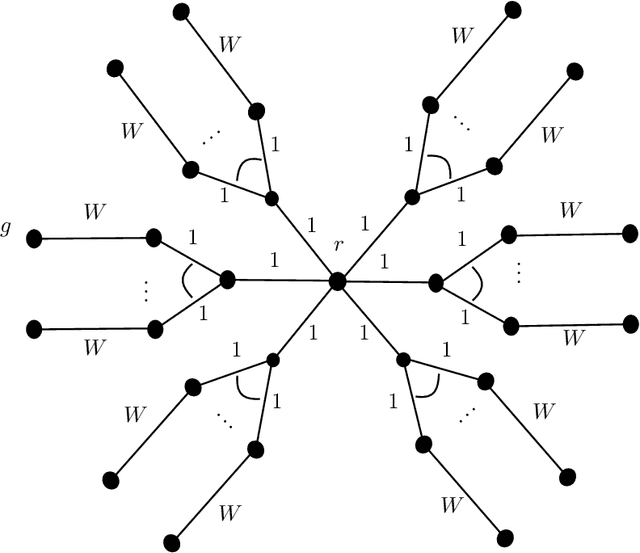
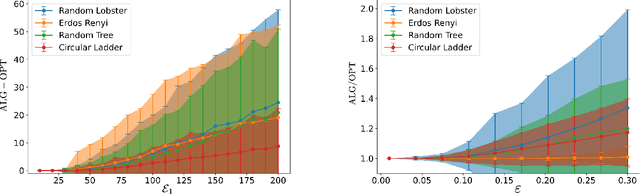
We consider the problem of graph searching with prediction recently introduced by Banerjee et al. (2022). In this problem, an agent, starting at some vertex $r$ has to traverse a (potentially unknown) graph $G$ to find a hidden goal node $g$ while minimizing the total distance travelled. We study a setting in which at any node $v$, the agent receives a noisy estimate of the distance from $v$ to $g$. We design algorithms for this search task on unknown graphs. We establish the first formal guarantees on unknown weighted graphs and provide lower bounds showing that the algorithms we propose have optimal or nearly-optimal dependence on the prediction error. Further, we perform numerical experiments demonstrating that in addition to being robust to adversarial error, our algorithms perform well in typical instances in which the error is stochastic. Finally, we provide alternative simpler performance bounds on the algorithms of Banerjee et al. (2022) for the case of searching on a known graph, and establish new lower bounds for this setting.

Error-Tolerant Exact Query Learning of Finite Set Partitions with Same-Cluster Oracle

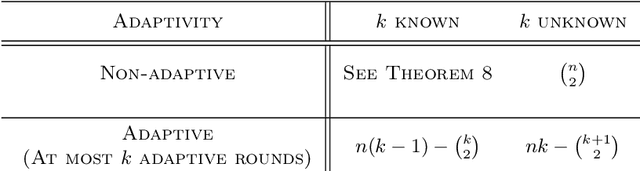
This paper initiates the study of active learning for exact recovery of partitions exclusively through access to a same-cluster oracle in the presence of bounded adversarial error. We first highlight a novel connection between learning partitions and correlation clustering. Then we use this connection to build a R\'enyi-Ulam style analytical framework for this problem, and prove upper and lower bounds on its worst-case query complexity. Further, we bound the expected performance of a relevant randomized algorithm. Finally, we study the relationship between adaptivity and query complexity for this problem and related variants.