Assemblies of neurons can learn to classify well-separated distributions
Paper and Code
Oct 07, 2021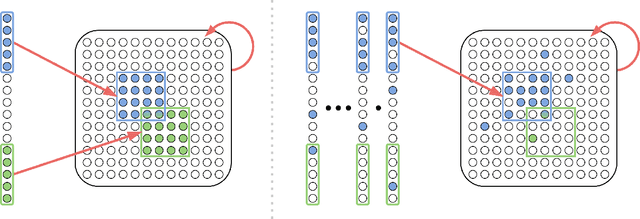
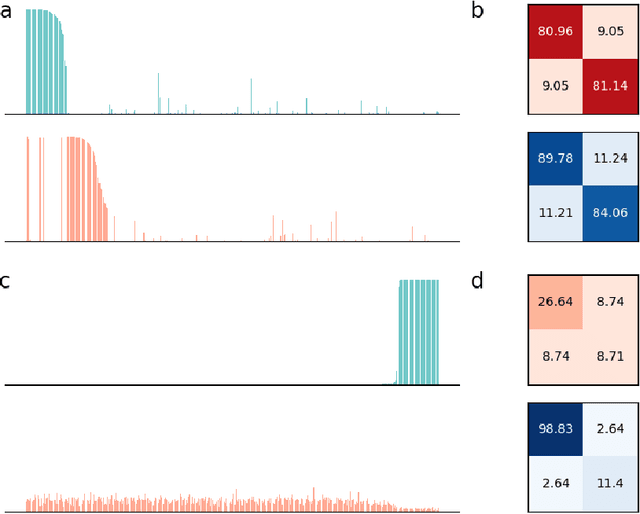

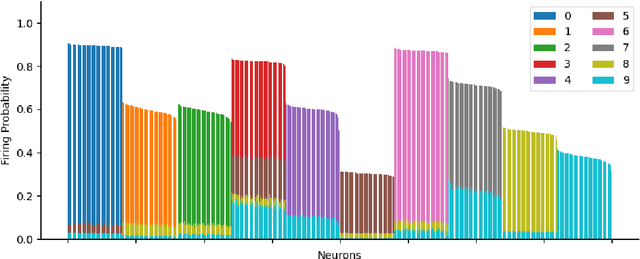
Assemblies are patterns of coordinated firing across large populations of neurons, believed to represent higher-level information in the brain, such as memories, concepts, words, and other cognitive categories. Recently, a computational system called the Assembly Calculus (AC) has been proposed, based on a set of biologically plausible operations on assemblies. This system is capable of simulating arbitrary space-bounded computation, and describes quite naturally complex cognitive phenomena such as language. However, the question of whether assemblies can perform the brain's greatest trick -- its ability to learn -- has been open. We show that the AC provides a mechanism for learning to classify samples from well-separated classes. We prove rigorously that for simple classification problems, a new assembly that represents each class can be reliably formed in response to a few stimuli from it; this assembly is henceforth reliably recalled in response to new stimuli from the same class. Furthermore, such class assemblies will be distinguishable as long as the respective classes are reasonably separated, in particular when they are clusters of similar assemblies, or more generally divided by a halfspace with margin. Experimentally, we demonstrate the successful formation of assemblies which represent concept classes on synthetic data drawn from these distributions, and also on MNIST, which lends itself to classification through one assembly per digit. Seen as a learning algorithm, this mechanism is entirely online, generalizes from very few samples, and requires only mild supervision -- all key attributes of learning in a model of the brain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge