A Behavior Tree-inspired programming language for autonomous agents

We propose a design for a functional programming language for autonomous agents, built off the ideas and motivations of Behavior Trees (BTs). BTs are a popular model for designing agents behavior in robotics and AI. However, as their growth has increased dramatically, the simple model of BTs has come to be limiting. There is a growing push to increase the functionality of BTs, with the end goal of BTs evolving into a programming language in their own right, centred around the defining BT properties of modularity and reactiveness. In this paper, we examine how the BT model must be extended in order to grow into such a language. We identify some fundamental problems which must be solved: implementing `reactive' selection, 'monitoring' safety-critical conditions, and passing data between actions. We provide a variety of small examples which demonstrate that these problems are complex, and that current BT approaches do not handle them in a manner consistent with modularity. We instead provide a simple set of modular programming primitives for handling these use cases, and show how they can be combined to build complex programs. We present a full specification for our BT-inspired language, and give an implementation in the functional programming language Haskell. Finally, we demonstrate our language by translating a large and complex BT into a simple, unambiguous program.

The Replicator Dynamic, Chain Components and the Response Graph

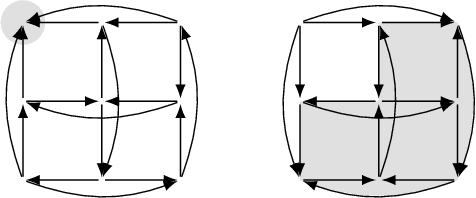
In this paper we examine the relationship between the flow of the replicator dynamic, the continuum limit of Multiplicative Weights Update, and a game's response graph. We settle an open problem establishing that under the replicator, sink chain components -- a topological notion of long-run outcome of a dynamical system -- always exist and are approximated by the sink connected components of the game's response graph. More specifically, each sink chain component contains a sink connected component of the response graph, as well as all mixed strategy profiles whose support consists of pure profiles in the same connected component, a set we call the content of the connected component. As a corollary, all profiles are chain recurrent in games with strongly connected response graphs. In any two-player game sharing a response graph with a zero-sum game, the sink chain component is unique. In two-player zero-sum and potential games the sink chain components and sink connected components are in a one-to-one correspondence, and we conjecture that this holds in all games.

An expressiveness hierarchy of Behavior Trees and related architectures

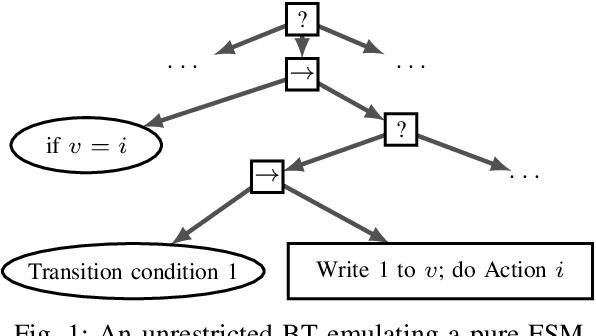
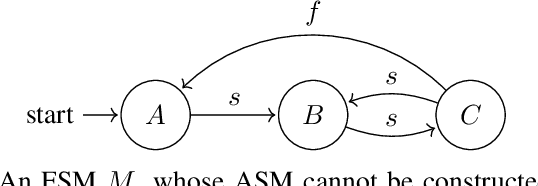
In this paper we provide a formal framework for comparing the expressive power of Behavior Trees (BTs) to other action selection architectures. Taking inspiration from the analogous comparisons of structural programming methodologies, we formalise the concept of `expressiveness'. This leads us to an expressiveness hierarchy of control architectures, which includes BTs, Decision Trees (DTs), Teleo-reactive Programs (TRs) and Finite State Machines (FSMs). By distinguishing between BTs with auxiliary variables and those without, we demonstrate the existence of a trade-off in BT design between readability and expressiveness. We discuss what this means for BTs in practice.

On modularity in reactive control architectures, with an application to formal verification

Modularity is a central principle throughout the design process for cyber-physical systems. Modularity reduces complexity and increases reuse of behavior. In this paper we pose and answer the following question: how can we identify independent `modules' within the structure of reactive control architectures? To this end, we propose a graph-structured control architecture we call a decision structure, and show how it generalises some reactive control architectures which are popular in Artificial Intelligence (AI) and robotics, specifically Teleo-Reactive programs (TRs), Decision Trees (DTs), Behavior Trees (BTs) and Generalised Behavior Trees ($k$-BTs). Inspired by the definition of a module in graph theory, we define modules in decision structures and show how each decision structure possesses a canonical decomposition into its modules. We can naturally characterise each of the BTs, $k$-BTs, DTs and TRs by properties of their module decomposition. This allows us to recognise which decision structures are equivalent to each of these architectures in quadratic time. Our proposed concept of modules extends to formal verification, under any verification scheme capable of verifying a decision structure. Namely, we prove that a modification to a module within a decision structure has no greater flow-on effects than a modification to an individual action within that structure. This enables verification on modules to be done locally and hierarchically, where structures can be verified and then repeatedly locally modified, with modules replaced by modules while preserving correctness. To illustrate the findings, we present an example of a solar-powered drone controlled by a decision structure. We use a Linear Temporal Logic-based verification scheme to verify the correctness of this structure, and then show how one can modify modules while preserving its correctness.

A principled analysis of Behavior Trees and their generalisations

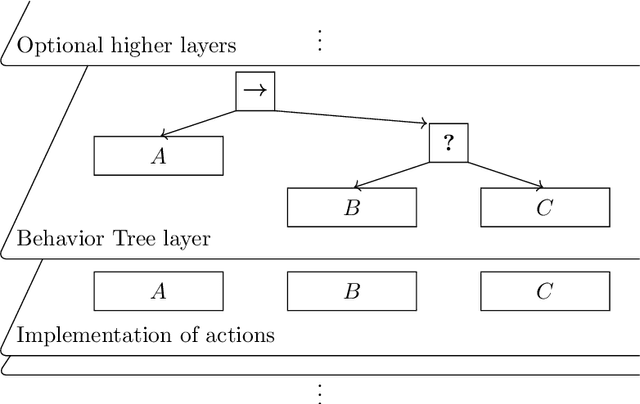
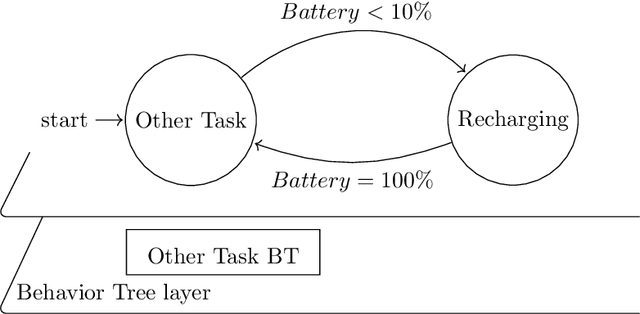
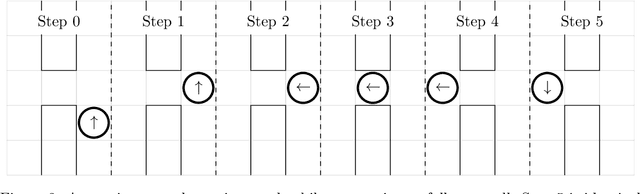
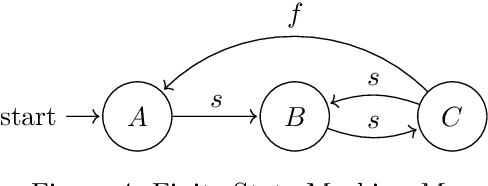
As complex autonomous robotic systems become more widespread, the goals of transparent and reusable Artificial Intelligence (AI) become more important. In this paper we analyse how the principles behind Behavior Trees (BTs), an increasingly popular tree-structured control architecture, are applicable to these goals. Using structured programming as a guide, we analyse the BT principles of reactiveness and modularity in a formal framework of action selection. Proceeding from these principles, we review a number of challenging use-cases of BTs in the literature, and show that reasoning via these principles leads to compatible solutions. Extending these arguments, we introduce a new class of control architectures we call generalised BTs or $k$-BTs and show how they can extend the applicability of BTs to some of the aforementioned challenging BT use-cases while preserving the BT principles. We compare BTs to a number of other control architectures within this framework, and show which forms of decision-making can and cannot be equivalently represented by BTs. This allows us to construct a hierarchy of architectures and to show how BTs fit into such a hierarchy.