System-2 Recommenders: Disentangling Utility and Engagement in Recommendation Systems via Temporal Point-Processes

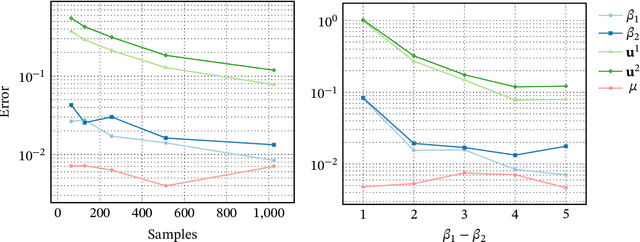
Recommender systems are an important part of the modern human experience whose influence ranges from the food we eat to the news we read. Yet, there is still debate as to what extent recommendation platforms are aligned with the user goals. A core issue fueling this debate is the challenge of inferring a user utility based on engagement signals such as likes, shares, watch time etc., which are the primary metric used by platforms to optimize content. This is because users utility-driven decision-processes (which we refer to as System-2), e.g., reading news that are relevant for them, are often confounded by their impulsive decision-processes (which we refer to as System-1), e.g., spend time on click-bait news. As a result, it is difficult to infer whether an observed engagement is utility-driven or impulse-driven. In this paper we explore a new approach to recommender systems where we infer user utility based on their return probability to the platform rather than engagement signals. Our intuition is that users tend to return to a platform in the long run if it creates utility for them, while pure engagement-driven interactions that do not add utility, may affect user return in the short term but will not have a lasting effect. We propose a generative model in which past content interactions impact the arrival rates of users based on a self-exciting Hawkes process. These arrival rates to the platform are a combination of both System-1 and System-2 decision processes. The System-2 arrival intensity depends on the utility and has a long lasting effect, while the System-1 intensity depends on the instantaneous gratification and tends to vanish rapidly. We show analytically that given samples it is possible to disentangle System-1 and System-2 and allow content optimization based on user utility. We conduct experiments on synthetic data to demonstrate the effectiveness of our approach.

Optimal and Adaptive Non-Stationary Dueling Bandits Under a Generalized Borda Criterion

In dueling bandits, the learner receives preference feedback between arms, and the regret of an arm is defined in terms of its suboptimality to a winner arm. The more challenging and practically motivated non-stationary variant of dueling bandits, where preferences change over time, has been the focus of several recent works (Saha and Gupta, 2022; Buening and Saha, 2023; Suk and Agarwal, 2023). The goal is to design algorithms without foreknowledge of the amount of change. The bulk of known results here studies the Condorcet winner setting, where an arm preferred over any other exists at all times. Yet, such a winner may not exist and, to contrast, the Borda version of this problem (which is always well-defined) has received little attention. In this work, we establish the first optimal and adaptive Borda dynamic regret upper bound, which highlights fundamental differences in the learnability of severe non-stationarity between Condorcet vs. Borda regret objectives in dueling bandits. Surprisingly, our techniques for non-stationary Borda dueling bandits also yield improved rates within the Condorcet winner setting, and reveal new preference models where tighter notions of non-stationarity are adaptively learnable. This is accomplished through a novel generalized Borda score framework which unites the Borda and Condorcet problems, thus allowing reduction of Condorcet regret to a Borda-like task. Such a generalization was not previously known and is likely to be of independent interest.

Scalable, Simulation-Guided Compliant Tactile Finger Design

Compliant grippers enable robots to work with humans in unstructured environments. In general, these grippers can improve with tactile sensing to estimate the state of objects around them to precisely manipulate objects. However, co-designing compliant structures with high-resolution tactile sensing is a challenging task. We propose a simulation framework for the end-to-end forward design of GelSight Fin Ray sensors. Our simulation framework consists of mechanical simulation using the finite element method (FEM) and optical simulation including physically based rendering (PBR). To simulate the fluorescent paint used in these GelSight Fin Rays, we propose an efficient method that can be directly integrated in PBR. Using the simulation framework, we investigate design choices available in the compliant grippers, namely gel pad shapes, illumination conditions, Fin Ray gripper sizes, and Fin Ray stiffness. This infrastructure enables faster design and prototype time frames of new Fin Ray sensors that have various sensing areas, ranging from 48 mm $\times$ \18 mm to 70 mm $\times$ 35 mm. Given the parameters we choose, we can thus optimize different Fin Ray designs and show their utility in grasping day-to-day objects.

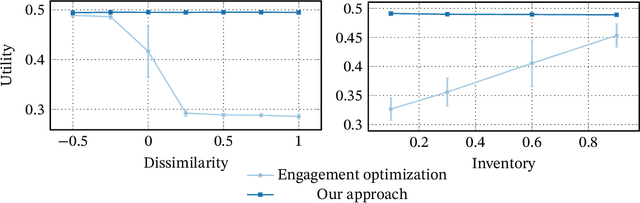
Misalignment, Learning, and Ranking: Harnessing Users Limited Attention

In digital health and EdTech, recommendation systems face a significant challenge: users often choose impulsively, in ways that conflict with the platform's long-term payoffs. This misalignment makes it difficult to effectively learn to rank items, as it may hinder exploration of items with greater long-term payoffs. Our paper tackles this issue by utilizing users' limited attention spans. We propose a model where a platform presents items with unknown payoffs to the platform in a ranked list to $T$ users over time. Each user selects an item by first considering a prefix window of these ranked items and then picking the highest preferred item in that window (and the platform observes its payoff for this item). We study the design of online bandit algorithms that obtain vanishing regret against hindsight optimal benchmarks. We first consider adversarial window sizes and stochastic iid payoffs. We design an active-elimination-based algorithm that achieves an optimal instance-dependent regret bound of $O(\log(T))$, by showing matching regret upper and lower bounds. The key idea is using the combinatorial structure of the problem to either obtain a large payoff from each item or to explore by getting a sample from that item. This method systematically narrows down the item choices to enhance learning efficiency and payoff. Second, we consider adversarial payoffs and stochastic iid window sizes. We start from the full-information problem of finding the permutation that maximizes the expected payoff. By a novel combinatorial argument, we characterize the polytope of admissible item selection probabilities by a permutation and show it has a polynomial-size representation. Using this representation, we show how standard algorithms for adversarial online linear optimization in the space of admissible probabilities can be used to obtain a polynomial-time algorithm with $O(\sqrt{T})$ regret.

Semi-Bandit Learning for Monotone Stochastic Optimization

Stochastic optimization is a widely used approach for optimization under uncertainty, where uncertain input parameters are modeled by random variables. Exact or approximation algorithms have been obtained for several fundamental problems in this area. However, a significant limitation of this approach is that it requires full knowledge of the underlying probability distributions. Can we still get good (approximation) algorithms if these distributions are unknown, and the algorithm needs to learn them through repeated interactions? In this paper, we resolve this question for a large class of "monotone" stochastic problems, by providing a generic online learning algorithm with $\sqrt{T \log T}$ regret relative to the best approximation algorithm (under known distributions). Importantly, our online algorithm works in a semi-bandit setting, where in each period, the algorithm only observes samples from the r.v.s that were actually probed. Our framework applies to several fundamental problems in stochastic optimization such as prophet inequality, Pandora's box, stochastic knapsack, stochastic matchings and stochastic submodular optimization.

Robotic Defect Inspection with Visual and Tactile Perception for Large-scale Components

In manufacturing processes, surface inspection is a key requirement for quality assessment and damage localization. Due to this, automated surface anomaly detection has become a promising area of research in various industrial inspection systems. A particular challenge in industries with large-scale components, like aircraft and heavy machinery, is inspecting large parts with very small defect dimensions. Moreover, these parts can be of curved shapes. To address this challenge, we present a 2-stage multi-modal inspection pipeline with visual and tactile sensing. Our approach combines the best of both visual and tactile sensing by identifying and localizing defects using a global view (vision) and using the localized area for tactile scanning for identifying remaining defects. To benchmark our approach, we propose a novel real-world dataset with multiple metallic defect types per image, collected in the production environments on real aerospace manufacturing parts, as well as online robot experiments in two environments. Our approach is able to identify 85% defects using Stage I and identify 100% defects after Stage II. The dataset is publicly available at https://zenodo.org/record/8327713

When Can We Track Significant Preference Shifts in Dueling Bandits?

The $K$-armed dueling bandits problem, where the feedback is in the form of noisy pairwise preferences, has been widely studied due its applications in information retrieval, recommendation systems, etc. Motivated by concerns that user preferences/tastes can evolve over time, we consider the problem of dueling bandits with distribution shifts. Specifically, we study the recent notion of significant shifts (Suk and Kpotufe, 2022), and ask whether one can design an adaptive algorithm for the dueling problem with $O(\sqrt{K\tilde{L}T})$ dynamic regret, where $\tilde{L}$ is the (unknown) number of significant shifts in preferences. We show that the answer to this question depends on the properties of underlying preference distributions. Firstly, we give an impossibility result that rules out any algorithm with $O(\sqrt{K\tilde{L}T})$ dynamic regret under the well-studied Condorcet and SST classes of preference distributions. Secondly, we show that $\text{SST} \cap \text{STI}$ is the largest amongst popular classes of preference distributions where it is possible to design such an algorithm. Overall, our results provides an almost complete resolution of the above question for the hierarchy of distribution classes.

Online Recommendations for Agents with Discounted Adaptive Preferences

For domains in which a recommender provides repeated content suggestions, agent preferences may evolve over time as a function of prior recommendations, and algorithms must take this into account for long-run optimization. Recently, Agarwal and Brown (2022) introduced a model for studying recommendations when agents' preferences are adaptive, and gave a series of results for the case when agent preferences depend {\it uniformly} on their history of past selections. Here, the recommender shows a $k$-item menu (out of $n$) to the agent at each round, who selects one of the $k$ items via their history-dependent {\it preference model}, yielding a per-item adversarial reward for the recommender. We expand this setting to {\it non-uniform} preferences, and give a series of results for {\it $\gamma$-discounted} histories. For this problem, the feasible regret benchmarks can depend drastically on varying conditions. In the ``large $\gamma$'' regime, we show that the previously considered benchmark, the ``EIRD set'', is attainable for any {\it smooth} model, relaxing the ``local learnability'' requirement from the uniform memory case. We introduce ``pseudo-increasing'' preference models, for which we give an algorithm which can compete against any item distribution with small uniform noise (the ``smoothed simplex''). We show NP-hardness results for larger regret benchmarks in each case. We give another algorithm for pseudo-increasing models (under a restriction on the adversarial nature of the reward functions), which works for any $\gamma$ and is faster when $\gamma$ is sufficiently small, and we show a super-polynomial regret lower bound with respect to EIRD for general models in the ``small $\gamma$'' regime. We conclude with a pair of algorithms for the memoryless case.

An Asymptotically Optimal Batched Algorithm for the Dueling Bandit Problem

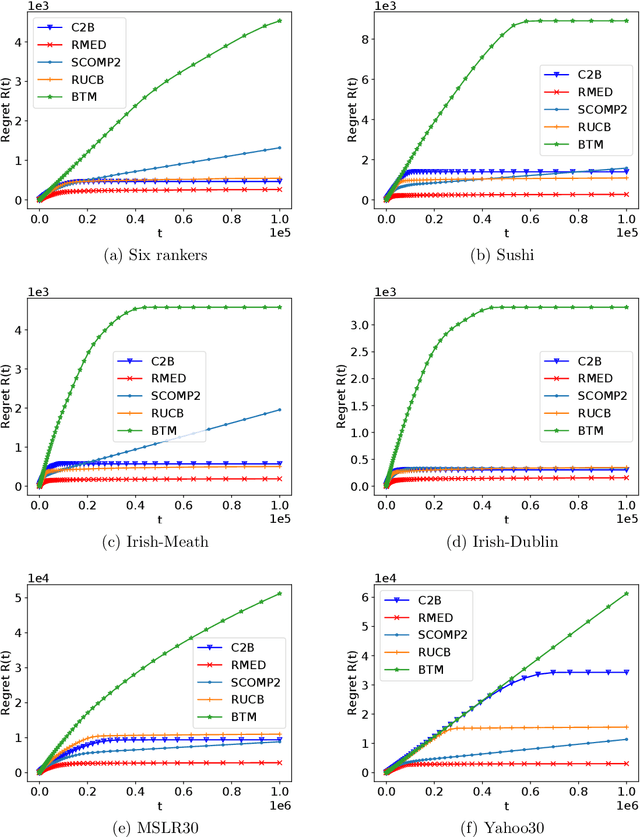
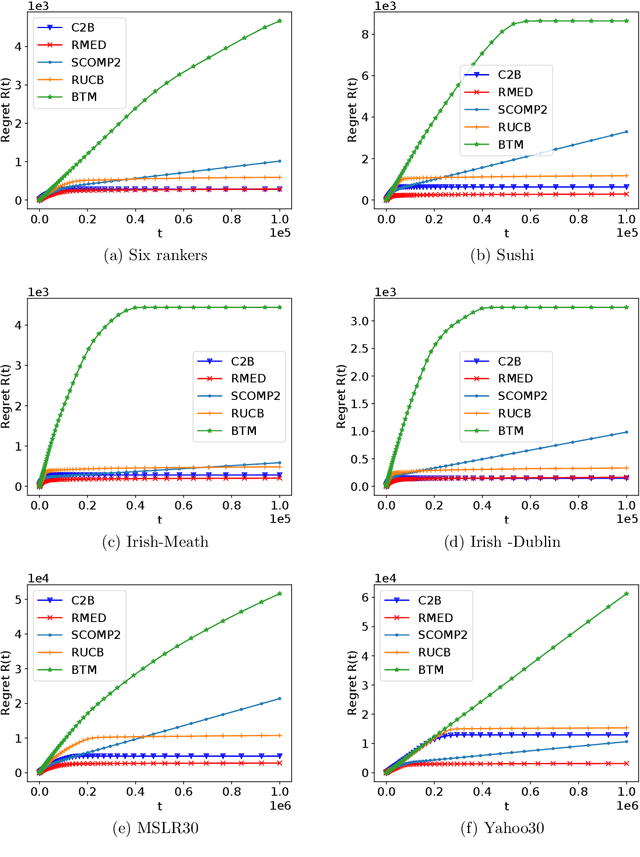
We study the $K$-armed dueling bandit problem, a variation of the traditional multi-armed bandit problem in which feedback is obtained in the form of pairwise comparisons. Previous learning algorithms have focused on the $\textit{fully adaptive}$ setting, where the algorithm can make updates after every comparison. The "batched" dueling bandit problem is motivated by large-scale applications like web search ranking and recommendation systems, where performing sequential updates may be infeasible. In this work, we ask: $\textit{is there a solution using only a few adaptive rounds that matches the asymptotic regret bounds of the best sequential algorithms for $K$-armed dueling bandits?}$ We answer this in the affirmative $\textit{under the Condorcet condition}$, a standard setting of the $K$-armed dueling bandit problem. We obtain asymptotic regret of $O(K^2\log^2(K)) + O(K\log(T))$ in $O(\log(T))$ rounds, where $T$ is the time horizon. Our regret bounds nearly match the best regret bounds known in the fully sequential setting under the Condorcet condition. Finally, in computational experiments over a variety of real-world datasets, we observe that our algorithm using $O(\log(T))$ rounds achieves almost the same performance as fully sequential algorithms (that use $T$ rounds).

Grasp Stability Prediction with Sim-to-Real Transfer from Tactile Sensing

Robot simulation has been an essential tool for data-driven manipulation tasks. However, most existing simulation frameworks lack either efficient and accurate models of physical interactions with tactile sensors or realistic tactile simulation. This makes the sim-to-real transfer for tactile-based manipulation tasks still challenging. In this work, we integrate simulation of robot dynamics and vision-based tactile sensors by modeling the physics of contact. This contact model uses simulated contact forces at the robot's end-effector to inform the generation of realistic tactile outputs. To eliminate the sim-to-real transfer gap, we calibrate our physics simulator of robot dynamics, contact model, and tactile optical simulator with real-world data, and then we demonstrate the effectiveness of our system on a zero-shot sim-to-real grasp stability prediction task where we achieve an average accuracy of 90.7% on various objects. Experiments reveal the potential of applying our simulation framework to more complicated manipulation tasks. We open-source our simulation framework at https://github.com/CMURoboTouch/Taxim/tree/taxim-robot.