Prathamesh Patil
Misalignment, Learning, and Ranking: Harnessing Users Limited Attention
Feb 21, 2024Abstract:In digital health and EdTech, recommendation systems face a significant challenge: users often choose impulsively, in ways that conflict with the platform's long-term payoffs. This misalignment makes it difficult to effectively learn to rank items, as it may hinder exploration of items with greater long-term payoffs. Our paper tackles this issue by utilizing users' limited attention spans. We propose a model where a platform presents items with unknown payoffs to the platform in a ranked list to $T$ users over time. Each user selects an item by first considering a prefix window of these ranked items and then picking the highest preferred item in that window (and the platform observes its payoff for this item). We study the design of online bandit algorithms that obtain vanishing regret against hindsight optimal benchmarks. We first consider adversarial window sizes and stochastic iid payoffs. We design an active-elimination-based algorithm that achieves an optimal instance-dependent regret bound of $O(\log(T))$, by showing matching regret upper and lower bounds. The key idea is using the combinatorial structure of the problem to either obtain a large payoff from each item or to explore by getting a sample from that item. This method systematically narrows down the item choices to enhance learning efficiency and payoff. Second, we consider adversarial payoffs and stochastic iid window sizes. We start from the full-information problem of finding the permutation that maximizes the expected payoff. By a novel combinatorial argument, we characterize the polytope of admissible item selection probabilities by a permutation and show it has a polynomial-size representation. Using this representation, we show how standard algorithms for adversarial online linear optimization in the space of admissible probabilities can be used to obtain a polynomial-time algorithm with $O(\sqrt{T})$ regret.
Sublinear Algorithms for Hierarchical Clustering
Jun 15, 2022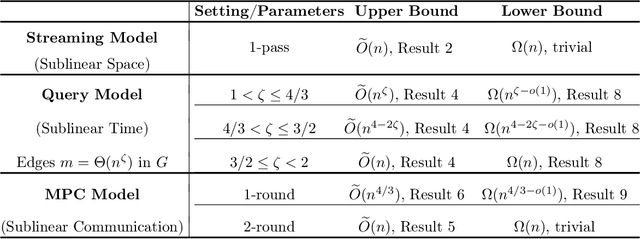
Abstract:Hierarchical clustering over graphs is a fundamental task in data mining and machine learning with applications in domains such as phylogenetics, social network analysis, and information retrieval. Specifically, we consider the recently popularized objective function for hierarchical clustering due to Dasgupta. Previous algorithms for (approximately) minimizing this objective function require linear time/space complexity. In many applications the underlying graph can be massive in size making it computationally challenging to process the graph even using a linear time/space algorithm. As a result, there is a strong interest in designing algorithms that can perform global computation using only sublinear resources. The focus of this work is to study hierarchical clustering for massive graphs under three well-studied models of sublinear computation which focus on space, time, and communication, respectively, as the primary resources to optimize: (1) (dynamic) streaming model where edges are presented as a stream, (2) query model where the graph is queried using neighbor and degree queries, (3) MPC model where the graph edges are partitioned over several machines connected via a communication channel. We design sublinear algorithms for hierarchical clustering in all three models above. At the heart of our algorithmic results is a view of the objective in terms of cuts in the graph, which allows us to use a relaxed notion of cut sparsifiers to do hierarchical clustering while introducing only a small distortion in the objective function. Our main algorithmic contributions are then to show how cut sparsifiers of the desired form can be efficiently constructed in the query model and the MPC model. We complement our algorithmic results by establishing nearly matching lower bounds that rule out the possibility of designing better algorithms in each of these models.
A Sharp Memory-Regret Trade-Off for Multi-Pass Streaming Bandits
May 02, 2022Abstract:The stochastic $K$-armed bandit problem has been studied extensively due to its applications in various domains ranging from online advertising to clinical trials. In practice however, the number of arms can be very large resulting in large memory requirements for simultaneously processing them. In this paper we consider a streaming setting where the arms are presented in a stream and the algorithm uses limited memory to process these arms. Here, the goal is not only to minimize regret, but also to do so in minimal memory. Previous algorithms for this problem operate in one of the two settings: they either use $\Omega(\log \log T)$ passes over the stream (Rathod, 2021; Chaudhuri and Kalyanakrishnan, 2020; Liau et al., 2018), or just a single pass (Maiti et al., 2021). In this paper we study the trade-off between memory and regret when $B$ passes over the stream are allowed, for any $B \geq 1$, and establish tight regret upper and lower bounds for any $B$-pass algorithm. Our results uncover a surprising *sharp transition phenomenon*: $O(1)$ memory is sufficient to achieve $\widetilde\Theta\Big(T^{\frac{1}{2} + \frac{1}{2^{B+2}-2}}\Big)$ regret in $B$ passes, and increasing the memory to any quantity that is $o(K)$ has almost no impact on further reducing this regret, unless we use $\Omega(K)$ memory. Our main technical contribution is our lower bound which requires the use of information-theoretic techniques as well as ideas from round elimination to show that the *residual problem* remains challenging over subsequent passes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge