Sublinear Algorithms for Hierarchical Clustering
Paper and Code
Jun 15, 2022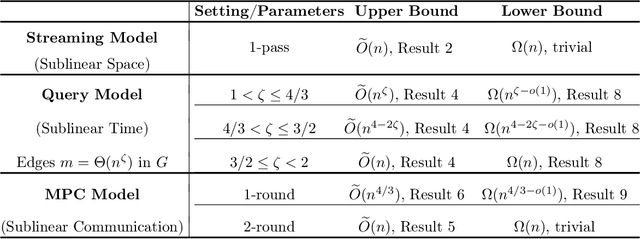
Hierarchical clustering over graphs is a fundamental task in data mining and machine learning with applications in domains such as phylogenetics, social network analysis, and information retrieval. Specifically, we consider the recently popularized objective function for hierarchical clustering due to Dasgupta. Previous algorithms for (approximately) minimizing this objective function require linear time/space complexity. In many applications the underlying graph can be massive in size making it computationally challenging to process the graph even using a linear time/space algorithm. As a result, there is a strong interest in designing algorithms that can perform global computation using only sublinear resources. The focus of this work is to study hierarchical clustering for massive graphs under three well-studied models of sublinear computation which focus on space, time, and communication, respectively, as the primary resources to optimize: (1) (dynamic) streaming model where edges are presented as a stream, (2) query model where the graph is queried using neighbor and degree queries, (3) MPC model where the graph edges are partitioned over several machines connected via a communication channel. We design sublinear algorithms for hierarchical clustering in all three models above. At the heart of our algorithmic results is a view of the objective in terms of cuts in the graph, which allows us to use a relaxed notion of cut sparsifiers to do hierarchical clustering while introducing only a small distortion in the objective function. Our main algorithmic contributions are then to show how cut sparsifiers of the desired form can be efficiently constructed in the query model and the MPC model. We complement our algorithmic results by establishing nearly matching lower bounds that rule out the possibility of designing better algorithms in each of these models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge