Improved and Oracle-Efficient Online $\ell_1$-Multicalibration

We study \emph{online multicalibration}, a framework for ensuring calibrated predictions across multiple groups in adversarial settings, across $T$ rounds. Although online calibration is typically studied in the $\ell_1$ norm, prior approaches to online multicalibration have taken the indirect approach of obtaining rates in other norms (such as $\ell_2$ and $\ell_{\infty}$) and then transferred these guarantees to $\ell_1$ at additional loss. In contrast, we propose a direct method that achieves improved and oracle-efficient rates of $\widetilde{\mathcal{O}}(T^{-1/3})$ and $\widetilde{\mathcal{O}}(T^{-1/4})$ respectively, for online $\ell_1$-multicalibration. Our key insight is a novel reduction of online \(\ell_1\)-multicalibration to an online learning problem with product-based rewards, which we refer to as \emph{online linear-product optimization} ($\mathtt{OLPO}$). To obtain the improved rate of $\widetilde{\mathcal{O}}(T^{-1/3})$, we introduce a linearization of $\mathtt{OLPO}$ and design a no-regret algorithm for this linearized problem. Although this method guarantees the desired sublinear rate (nearly matching the best rate for online calibration), it becomes computationally expensive when the group family \(\mathcal{H}\) is large or infinite, since it enumerates all possible groups. To address scalability, we propose a second approach to $\mathtt{OLPO}$ that makes only a polynomial number of calls to an offline optimization (\emph{multicalibration evaluation}) oracle, resulting in \emph{oracle-efficient} online \(\ell_1\)-multicalibration with a rate of $\widetilde{\mathcal{O}}(T^{-1/4})$. Our framework also extends to certain infinite families of groups (e.g., all linear functions on the context space) by exploiting a $1$-Lipschitz property of the \(\ell_1\)-multicalibration error with respect to \(\mathcal{H}\).

Single-Sample and Robust Online Resource Allocation

Online Resource Allocation problem is a central problem in many areas of Computer Science, Operations Research, and Economics. In this problem, we sequentially receive $n$ stochastic requests for $m$ kinds of shared resources, where each request can be satisfied in multiple ways, consuming different amounts of resources and generating different values. The goal is to achieve a $(1-\epsilon)$-approximation to the hindsight optimum, where $\epsilon>0$ is a small constant, assuming each resource has a large budget. In this paper, we investigate the learnability and robustness of online resource allocation. Our primary contribution is a novel Exponential Pricing algorithm with the following properties: 1. It requires only a \emph{single sample} from each of the $n$ request distributions to achieve a $(1-\epsilon)$-approximation for online resource allocation with large budgets. Such an algorithm was previously unknown, even with access to polynomially many samples, as prior work either assumed full distributional knowledge or was limited to i.i.d.\,or random-order arrivals. 2. It is robust to corruptions in the outliers model and the value augmentation model. Specifically, it maintains its $(1 - \epsilon)$-approximation guarantee under both these robustness models, resolving the open question posed in Argue, Gupta, Molinaro, and Singla (SODA'22). 3. It operates as a simple item-pricing algorithm that ensures incentive compatibility. The intuition behind our Exponential Pricing algorithm is that the price of a resource should adjust exponentially as it is overused or underused. It differs from conventional approaches that use an online learning algorithm for item pricing. This departure guarantees that the algorithm will never run out of any resource, but loses the usual no-regret properties of online learning algorithms, necessitating a new analytical approach.

Semi-Bandit Learning for Monotone Stochastic Optimization

Stochastic optimization is a widely used approach for optimization under uncertainty, where uncertain input parameters are modeled by random variables. Exact or approximation algorithms have been obtained for several fundamental problems in this area. However, a significant limitation of this approach is that it requires full knowledge of the underlying probability distributions. Can we still get good (approximation) algorithms if these distributions are unknown, and the algorithm needs to learn them through repeated interactions? In this paper, we resolve this question for a large class of "monotone" stochastic problems, by providing a generic online learning algorithm with $\sqrt{T \log T}$ regret relative to the best approximation algorithm (under known distributions). Importantly, our online algorithm works in a semi-bandit setting, where in each period, the algorithm only observes samples from the r.v.s that were actually probed. Our framework applies to several fundamental problems in stochastic optimization such as prophet inequality, Pandora's box, stochastic knapsack, stochastic matchings and stochastic submodular optimization.

An Asymptotically Optimal Batched Algorithm for the Dueling Bandit Problem

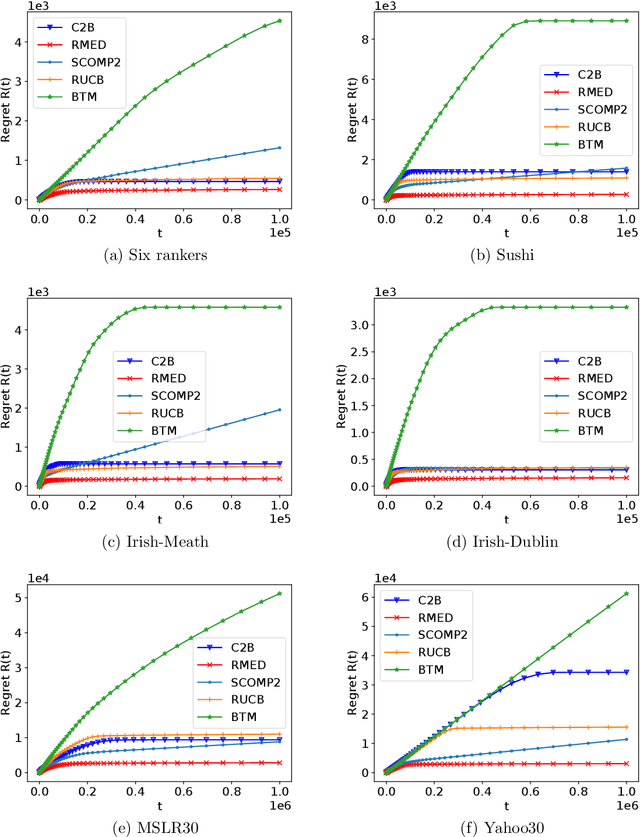
We study the $K$-armed dueling bandit problem, a variation of the traditional multi-armed bandit problem in which feedback is obtained in the form of pairwise comparisons. Previous learning algorithms have focused on the $\textit{fully adaptive}$ setting, where the algorithm can make updates after every comparison. The "batched" dueling bandit problem is motivated by large-scale applications like web search ranking and recommendation systems, where performing sequential updates may be infeasible. In this work, we ask: $\textit{is there a solution using only a few adaptive rounds that matches the asymptotic regret bounds of the best sequential algorithms for $K$-armed dueling bandits?}$ We answer this in the affirmative $\textit{under the Condorcet condition}$, a standard setting of the $K$-armed dueling bandit problem. We obtain asymptotic regret of $O(K^2\log^2(K)) + O(K\log(T))$ in $O(\log(T))$ rounds, where $T$ is the time horizon. Our regret bounds nearly match the best regret bounds known in the fully sequential setting under the Condorcet condition. Finally, in computational experiments over a variety of real-world datasets, we observe that our algorithm using $O(\log(T))$ rounds achieves almost the same performance as fully sequential algorithms (that use $T$ rounds).

Batched Dueling Bandits

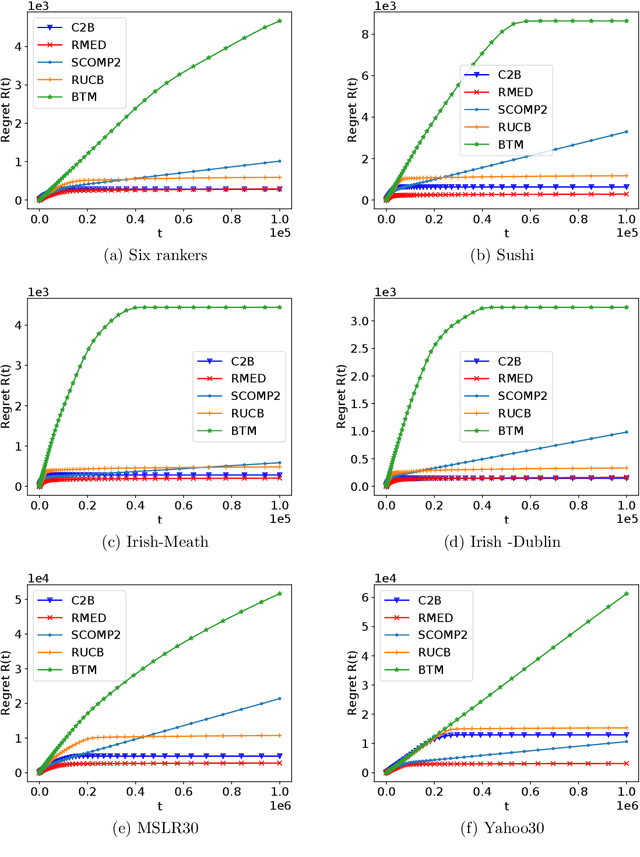
The $K$-armed dueling bandit problem, where the feedback is in the form of noisy pairwise comparisons, has been widely studied. Previous works have only focused on the sequential setting where the policy adapts after every comparison. However, in many applications such as search ranking and recommendation systems, it is preferable to perform comparisons in a limited number of parallel batches. We study the batched $K$-armed dueling bandit problem under two standard settings: (i) existence of a Condorcet winner, and (ii) strong stochastic transitivity and stochastic triangle inequality. For both settings, we obtain algorithms with a smooth trade-off between the number of batches and regret. Our regret bounds match the best known sequential regret bounds (up to poly-logarithmic factors), using only a logarithmic number of batches. We complement our regret analysis with a nearly-matching lower bound. Finally, we also validate our theoretical results via experiments on synthetic and real data.