Spatio-Spectral Graph Neural Networks

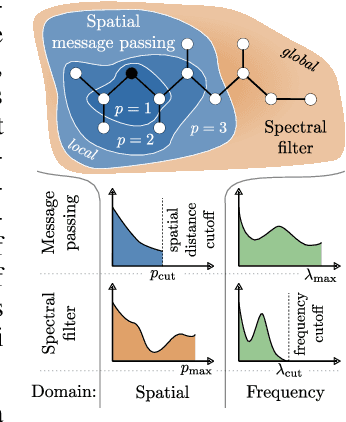
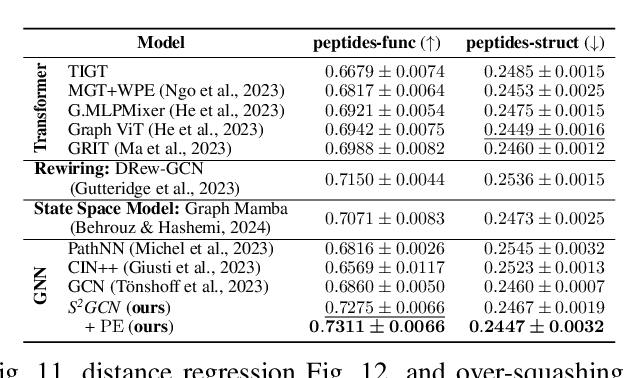
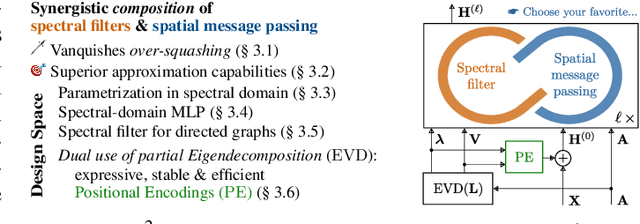
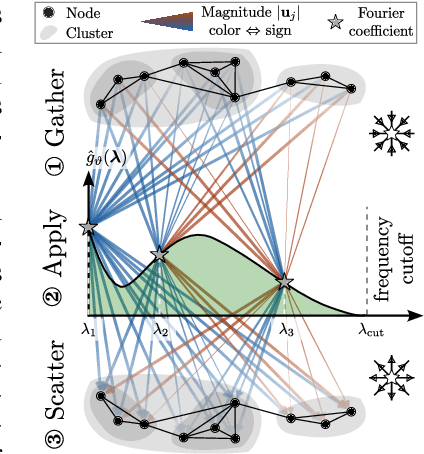
Spatial Message Passing Graph Neural Networks (MPGNNs) are widely used for learning on graph-structured data. However, key limitations of l-step MPGNNs are that their "receptive field" is typically limited to the l-hop neighborhood of a node and that information exchange between distant nodes is limited by over-squashing. Motivated by these limitations, we propose Spatio-Spectral Graph Neural Networks (S$^2$GNNs) -- a new modeling paradigm for Graph Neural Networks (GNNs) that synergistically combines spatially and spectrally parametrized graph filters. Parameterizing filters partially in the frequency domain enables global yet efficient information propagation. We show that S$^2$GNNs vanquish over-squashing and yield strictly tighter approximation-theoretic error bounds than MPGNNs. Further, rethinking graph convolutions at a fundamental level unlocks new design spaces. For example, S$^2$GNNs allow for free positional encodings that make them strictly more expressive than the 1-Weisfeiler-Lehman (WL) test. Moreover, to obtain general-purpose S$^2$GNNs, we propose spectrally parametrized filters for directed graphs. S$^2$GNNs outperform spatial MPGNNs, graph transformers, and graph rewirings, e.g., on the peptide long-range benchmark tasks, and are competitive with state-of-the-art sequence modeling. On a 40 GB GPU, S$^2$GNNs scale to millions of nodes.

Group Privacy Amplification and Unified Amplification by Subsampling for Rényi Differential Privacy

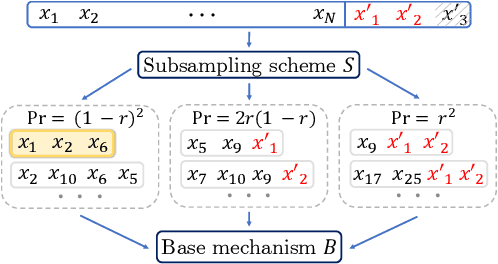
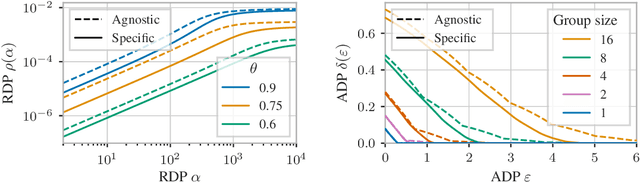
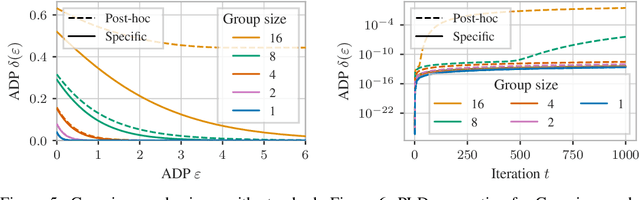
Differential privacy (DP) has various desirable properties, such as robustness to post-processing, group privacy, and amplification by subsampling, which can be derived independently of each other. Our goal is to determine whether stronger privacy guarantees can be obtained by considering multiple of these properties jointly. To this end, we focus on the combination of group privacy and amplification by subsampling. To provide guarantees that are amenable to machine learning algorithms, we conduct our analysis in the framework of R\'enyi-DP, which has more favorable composition properties than $(\epsilon,\delta)$-DP. As part of this analysis, we develop a unified framework for deriving amplification by subsampling guarantees for R\'enyi-DP, which represents the first such framework for a privacy accounting method and is of independent interest. We find that it not only lets us improve upon and generalize existing amplification results for R\'enyi-DP, but also derive provably tight group privacy amplification guarantees stronger than existing principles. These results establish the joint study of different DP properties as a promising research direction.

Ewald-based Long-Range Message Passing for Molecular Graphs

Neural architectures that learn potential energy surfaces from molecular data have undergone fast improvement in recent years. A key driver of this success is the Message Passing Neural Network (MPNN) paradigm. Its favorable scaling with system size partly relies upon a spatial distance limit on messages. While this focus on locality is a useful inductive bias, it also impedes the learning of long-range interactions such as electrostatics and van der Waals forces. To address this drawback, we propose Ewald message passing: a nonlocal Fourier space scheme which limits interactions via a cutoff on frequency instead of distance, and is theoretically well-founded in the Ewald summation method. It can serve as an augmentation on top of existing MPNN architectures as it is computationally cheap and agnostic to other architectural details. We test the approach with four baseline models and two datasets containing diverse periodic (OC20) and aperiodic structures (OE62). We observe robust improvements in energy mean absolute errors across all models and datasets, averaging 10% on OC20 and 16% on OE62. Our analysis shows an outsize impact of these improvements on structures with high long-range contributions to the ground truth energy.

Learning Integrable Dynamics with Action-Angle Networks

Machine learning has become increasingly popular for efficiently modelling the dynamics of complex physical systems, demonstrating a capability to learn effective models for dynamics which ignore redundant degrees of freedom. Learned simulators typically predict the evolution of the system in a step-by-step manner with numerical integration techniques. However, such models often suffer from instability over long roll-outs due to the accumulation of both estimation and integration error at each prediction step. Here, we propose an alternative construction for learned physical simulators that are inspired by the concept of action-angle coordinates from classical mechanics for describing integrable systems. We propose Action-Angle Networks, which learn a nonlinear transformation from input coordinates to the action-angle space, where evolution of the system is linear. Unlike traditional learned simulators, Action-Angle Networks do not employ any higher-order numerical integration methods, making them extremely efficient at modelling the dynamics of integrable physical systems.