AI-Driven Approaches for Glaucoma Detection -- A Comprehensive Review

The diagnosis of glaucoma plays a critical role in the management and treatment of this vision-threatening disease. Glaucoma is a group of eye diseases that cause blindness by damaging the optic nerve at the back of the eye. Often called "silent thief of sight", it exhibits no symptoms during the early stages. Therefore, early detection is crucial to prevent vision loss. With the rise of Artificial Intelligence (AI), particularly Deep Learning (DL) techniques, Computer-Aided Diagnosis (CADx) systems have emerged as promising tools to assist clinicians in accurately diagnosing glaucoma early. This paper aims to provide a comprehensive overview of AI techniques utilized in CADx systems for glaucoma diagnosis. Through a detailed analysis of current literature, we identify key gaps and challenges in these systems, emphasizing the need for improved safety, reliability, interpretability, and explainability. By identifying research gaps, we aim to advance the field of CADx systems especially for the early diagnosis of glaucoma, in order to prevent any potential loss of vision.

Certifiably Robust Encoding Schemes

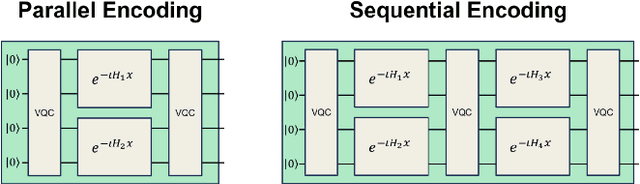
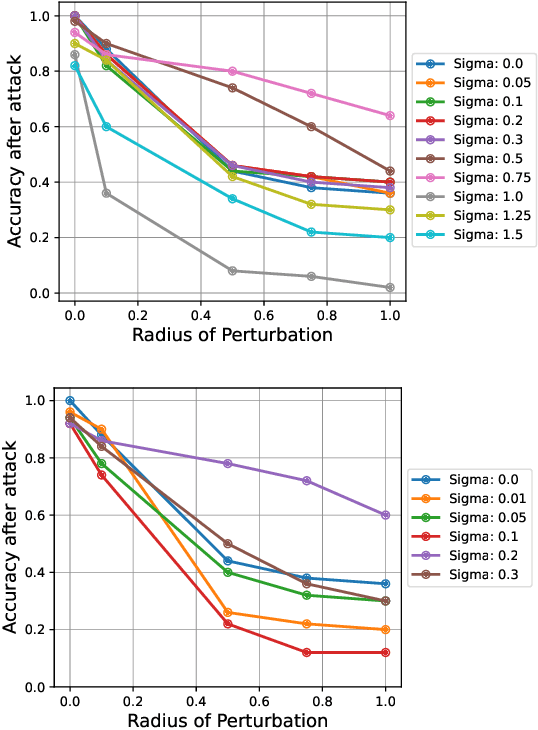
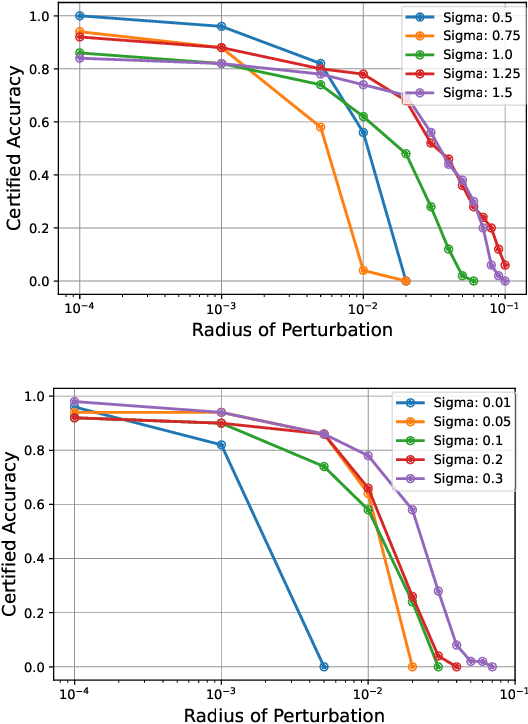
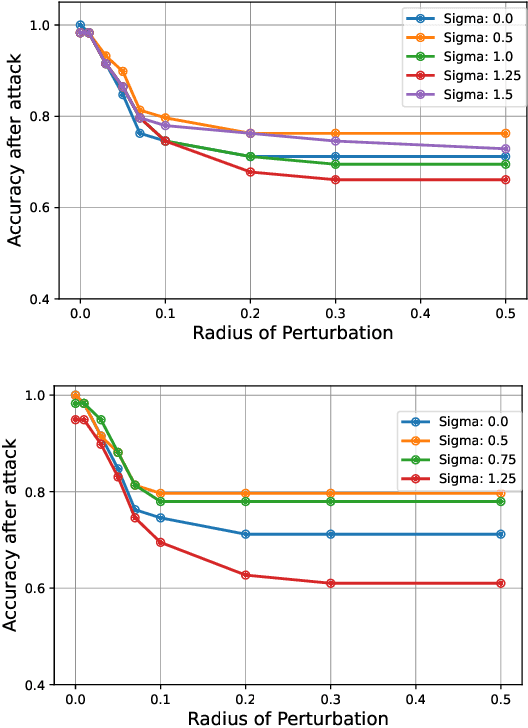
Quantum machine learning uses principles from quantum mechanics to process data, offering potential advances in speed and performance. However, previous work has shown that these models are susceptible to attacks that manipulate input data or exploit noise in quantum circuits. Following this, various studies have explored the robustness of these models. These works focus on the robustness certification of manipulations of the quantum states. We extend this line of research by investigating the robustness against perturbations in the classical data for a general class of data encoding schemes. We show that for such schemes, the addition of suitable noise channels is equivalent to evaluating the mean value of the noiseless classifier at the smoothed data, akin to Randomized Smoothing from classical machine learning. Using our general framework, we show that suitable additions of phase-damping noise channels improve empirical and provable robustness for the considered class of encoding schemes.

Discrete Randomized Smoothing Meets Quantum Computing

Breakthroughs in machine learning (ML) and advances in quantum computing (QC) drive the interdisciplinary field of quantum machine learning to new levels. However, due to the susceptibility of ML models to adversarial attacks, practical use raises safety-critical concerns. Existing Randomized Smoothing (RS) certification methods for classical machine learning models are computationally intensive. In this paper, we propose the combination of QC and the concept of discrete randomized smoothing to speed up the stochastic certification of ML models for discrete data. We show how to encode all the perturbations of the input binary data in superposition and use Quantum Amplitude Estimation (QAE) to obtain a quadratic reduction in the number of calls to the model that are required compared to traditional randomized smoothing techniques. In addition, we propose a new binary threat model to allow for an extensive evaluation of our approach on images, graphs, and text.

Quadratic Advantage with Quantum Randomized Smoothing Applied to Time-Series Analysis

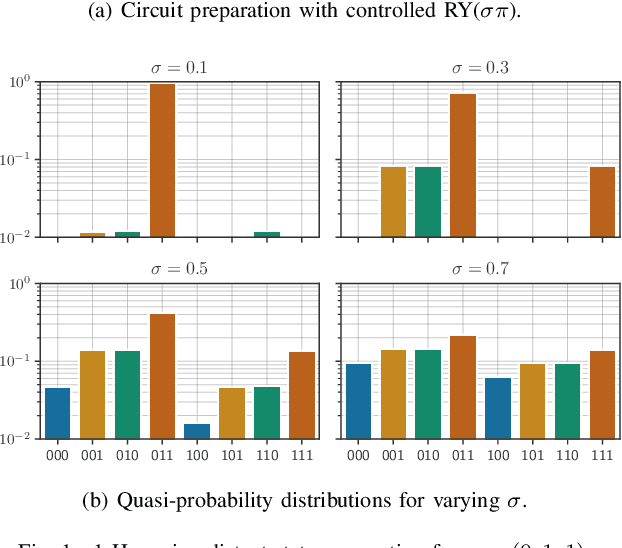
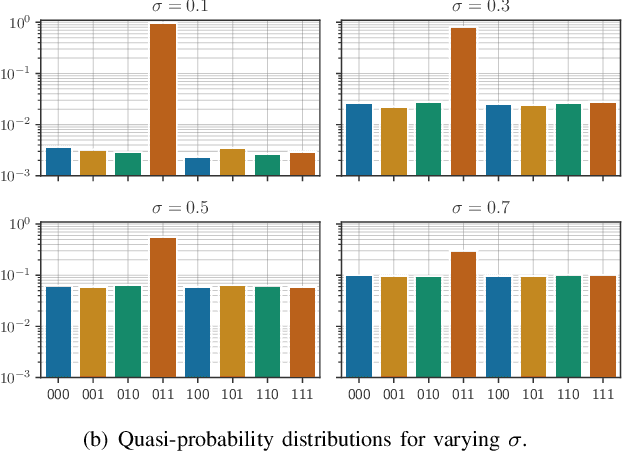
As quantum machine learning continues to develop at a rapid pace, the importance of ensuring the robustness and efficiency of quantum algorithms cannot be overstated. Our research presents an analysis of quantum randomized smoothing, how data encoding and perturbation modeling approaches can be matched to achieve meaningful robustness certificates. By utilizing an innovative approach integrating Grover's algorithm, a quadratic sampling advantage over classical randomized smoothing is achieved. This strategy necessitates a basis state encoding, thus restricting the space of meaningful perturbations. We show how constrained $k$-distant Hamming weight perturbations are a suitable noise distribution here, and elucidate how they can be constructed on a quantum computer. The efficacy of the proposed framework is demonstrated on a time series classification task employing a Bag-of-Words pre-processing solution. The advantage of quadratic sample reduction is recovered especially in the regime with large number of samples. This may allow quantum computers to efficiently scale randomized smoothing to more complex tasks beyond the reach of classical methods.

Building Continuous Quantum-Classical Bayesian Neural Networks for a Classical Clinical Dataset

In this work, we are introducing a Quantum-Classical Bayesian Neural Network (QCBNN) that is capable to perform uncertainty-aware classification of classical medical dataset. This model is a symbiosis of a classical Convolutional NN that performs ultra-sound image processing and a quantum circuit that generates its stochastic weights, within a Bayesian learning framework. To test the utility of this idea for the possible future deployment in the medical sector we track multiple behavioral metrics that capture both predictive performance as well as model's uncertainty. It is our ambition to create a hybrid model that is capable to classify samples in a more uncertainty aware fashion, which will advance the trustworthiness of these models and thus bring us step closer to utilizing them in the industry. We test multiple setups for quantum circuit for this task, and our best architectures display bigger uncertainty gap between correctly and incorrectly identified samples than its classical benchmark at an expense of a slight drop in predictive performance. The innovation of this paper is two-fold: (1) combining of different approaches that allow the stochastic weights from the quantum circuit to be continues thus allowing the model to classify application-driven dataset; (2) studying architectural features of quantum circuit that make-or-break these models, which pave the way into further investigation of more informed architectural designs.

Hamiltonian-based Quantum Reinforcement Learning for Neural Combinatorial Optimization

Advancements in Quantum Computing (QC) and Neural Combinatorial Optimization (NCO) represent promising steps in tackling complex computational challenges. On the one hand, Variational Quantum Algorithms such as QAOA can be used to solve a wide range of combinatorial optimization problems. On the other hand, the same class of problems can be solved by NCO, a method that has shown promising results, particularly since the introduction of Graph Neural Networks. Given recent advances in both research areas, we introduce Hamiltonian-based Quantum Reinforcement Learning (QRL), an approach at the intersection of QC and NCO. We model our ansatzes directly on the combinatorial optimization problem's Hamiltonian formulation, which allows us to apply our approach to a broad class of problems. Our ansatzes show favourable trainability properties when compared to the hardware efficient ansatzes, while also not being limited to graph-based problems, unlike previous works. In this work, we evaluate the performance of Hamiltonian-based QRL on a diverse set of combinatorial optimization problems to demonstrate the broad applicability of our approach and compare it to QAOA.

Quantum Patch-Based Autoencoder for Anomaly Segmentation

Quantum Machine Learning investigates the possibility of quantum computers enhancing Machine Learning algorithms. Anomaly segmentation is a fundamental task in various domains to identify irregularities at sample level and can be addressed with both supervised and unsupervised methods. Autoencoders are commonly used in unsupervised tasks, where models are trained to reconstruct normal instances efficiently, allowing anomaly identification through high reconstruction errors. While quantum autoencoders have been proposed in the literature, their application to anomaly segmentation tasks remains unexplored. In this paper, we introduce a patch-based quantum autoencoder (QPB-AE) for image anomaly segmentation, with a number of parameters scaling logarithmically with patch size. QPB-AE reconstructs the quantum state of the embedded input patches, computing an anomaly map directly from measurement through a SWAP test without reconstructing the input image. We evaluate its performance across multiple datasets and parameter configurations and compare it against a classical counterpart.

Constructing Optimal Noise Channels for Enhanced Robustness in Quantum Machine Learning

With the rapid advancement of Quantum Machine Learning (QML), the critical need to enhance security measures against adversarial attacks and protect QML models becomes increasingly evident. In this work, we outline the connection between quantum noise channels and differential privacy (DP), by constructing a family of noise channels which are inherently $\epsilon$-DP: $(\alpha, \gamma)$-channels. Through this approach, we successfully replicate the $\epsilon$-DP bounds observed for depolarizing and random rotation channels, thereby affirming the broad generality of our framework. Additionally, we use a semi-definite program to construct an optimally robust channel. In a small-scale experimental evaluation, we demonstrate the benefits of using our optimal noise channel over depolarizing noise, particularly in enhancing adversarial accuracy. Moreover, we assess how the variables $\alpha$ and $\gamma$ affect the certifiable robustness and investigate how different encoding methods impact the classifier's robustness.

Quantum Neural Networks under Depolarization Noise: Exploring White-Box Attacks and Defenses

Leveraging the unique properties of quantum mechanics, Quantum Machine Learning (QML) promises computational breakthroughs and enriched perspectives where traditional systems reach their boundaries. However, similarly to classical machine learning, QML is not immune to adversarial attacks. Quantum adversarial machine learning has become instrumental in highlighting the weak points of QML models when faced with adversarial crafted feature vectors. Diving deep into this domain, our exploration shines light on the interplay between depolarization noise and adversarial robustness. While previous results enhanced robustness from adversarial threats through depolarization noise, our findings paint a different picture. Interestingly, adding depolarization noise discontinued the effect of providing further robustness for a multi-class classification scenario. Consolidating our findings, we conducted experiments with a multi-class classifier adversarially trained on gate-based quantum simulators, further elucidating this unexpected behavior.

A Hyperparameter Study for Quantum Kernel Methods

Quantum kernel methods are a promising method in quantum machine learning thanks to the guarantees connected to them. Their accessibility for analytic considerations also opens up the possibility of prescreening datasets based on their potential for a quantum advantage. To do so, earlier works developed the geometric difference, which can be understood as a closeness measure between two kernel-based machine learning approaches, most importantly between a quantum kernel and classical kernel. This metric links the quantum and classical model complexities. Therefore, it raises the question of whether the geometric difference, based on its relation to model complexity, can be a useful tool in evaluations other than for the potential for quantum advantage. In this work, we investigate the effects of hyperparameter choice on the model performance and the generalization gap between classical and quantum kernels. The importance of hyperparameter optimization is well known also for classical machine learning. Especially for the quantum Hamiltonian evolution feature map, the scaling of the input data has been shown to be crucial. However, there are additional parameters left to be optimized, like the best number of qubits to trace out before computing a projected quantum kernel. We investigate the influence of these hyperparameters and compare the classically reliable method of cross validation with the method of choosing based on the geometric difference. Based on the thorough investigation of the hyperparameters across 11 datasets we identified commodities that can be exploited when examining a new dataset. In addition, our findings contribute to better understanding of the applicability of the geometric difference.