Quantum computer-enabled receivers for optical communication

Optical communication is the standard for high-bandwidth information transfer in today's digital age. The increasing demand for bandwidth has led to the maturation of coherent transceivers that use phase- and amplitude-modulated optical signals to encode more bits of information per transmitted pulse. Such encoding schemes achieve higher information density, but also require more complicated receivers to discriminate the signaling states. In fact, achieving the ultimate limit of optical communication capacity, especially in the low light regime, requires coherent joint detection of multiple pulses. Despite their superiority, such joint detection receivers are not in widespread use because of the difficulty of constructing them in the optical domain. In this work we describe how optomechanical transduction of phase information from coherent optical pulses to superconducting qubit states followed by the execution of trained short-depth variational quantum circuits can perform joint detection of communication codewords with error probabilities that surpass all classical, individual pulse detection receivers. Importantly, we utilize a model of optomechanical transduction that captures non-idealities such as thermal noise and loss in order to understand the transduction performance necessary to achieve a quantum advantage with such a scheme. We also execute the trained variational circuits on an IBM-Q device with the modeled transduced states as input to demonstrate that a quantum advantage is possible even with current levels of quantum computing hardware noise.

Shining light on data: Geometric data analysis through quantum dynamics

Experimental sciences have come to depend heavily on our ability to organize and interpret high-dimensional datasets. Natural laws, conservation principles, and inter-dependencies among observed variables yield geometric structure, with fewer degrees of freedom, on the dataset. We introduce the frameworks of semiclassical and microlocal analysis to data analysis and develop a novel, yet natural uncertainty principle for extracting fine-scale features of this geometric structure in data, crucially dependent on data-driven approximations to quantum mechanical processes underlying geometric optics. This leads to the first tractable algorithm for approximation of wave dynamics and geodesics on data manifolds with rigorous probabilistic convergence rates under the manifold hypothesis. We demonstrate our algorithm on real-world datasets, including an analysis of population mobility information during the COVID-19 pandemic to achieve four-fold improvement in dimensionality reduction over existing state-of-the-art and reveal anomalous behavior exhibited by less than 1.2% of the entire dataset. Our work initiates the study of data-driven quantum dynamics for analyzing datasets, and we outline several future directions for research.

Manifold learning via quantum dynamics

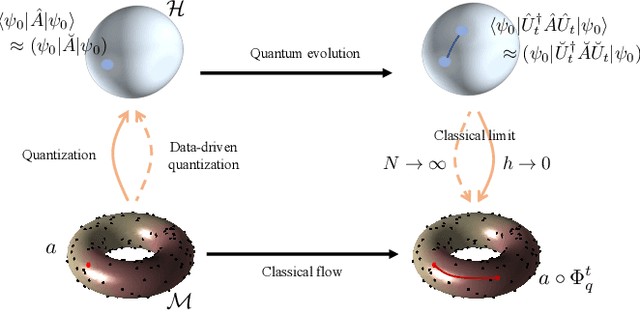
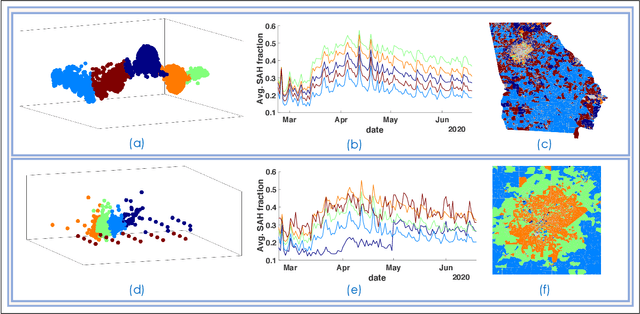
We introduce an algorithm for computing geodesics on sampled manifolds that relies on simulation of quantum dynamics on a graph embedding of the sampled data. Our approach exploits classic results in semiclassical analysis and the quantum-classical correspondence, and forms a basis for techniques to learn the manifold from which a dataset is sampled, and subsequently for nonlinear dimensionality reduction of high-dimensional datasets. We illustrate the new algorithm with data sampled from model manifolds and also by a clustering demonstration based on COVID-19 mobility data. Finally, our method reveals interesting connections between the discretization provided by data sampling and quantization.