A Review of Barren Plateaus in Variational Quantum Computing

Variational quantum computing offers a flexible computational paradigm with applications in diverse areas. However, a key obstacle to realizing their potential is the Barren Plateau (BP) phenomenon. When a model exhibits a BP, its parameter optimization landscape becomes exponentially flat and featureless as the problem size increases. Importantly, all the moving pieces of an algorithm -- choices of ansatz, initial state, observable, loss function and hardware noise -- can lead to BPs when ill-suited. Due to the significant impact of BPs on trainability, researchers have dedicated considerable effort to develop theoretical and heuristic methods to understand and mitigate their effects. As a result, the study of BPs has become a thriving area of research, influencing and cross-fertilizing other fields such as quantum optimal control, tensor networks, and learning theory. This article provides a comprehensive review of the current understanding of the BP phenomenon.

An analytic theory for the dynamics of wide quantum neural networks

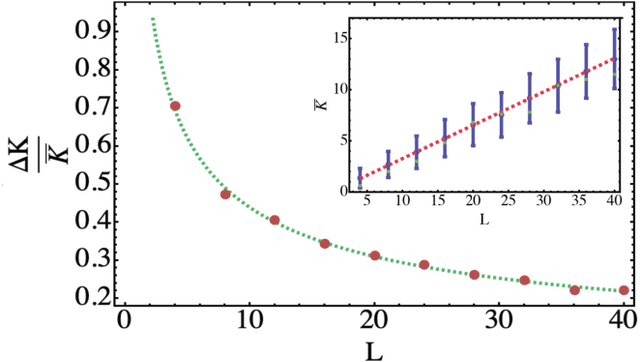
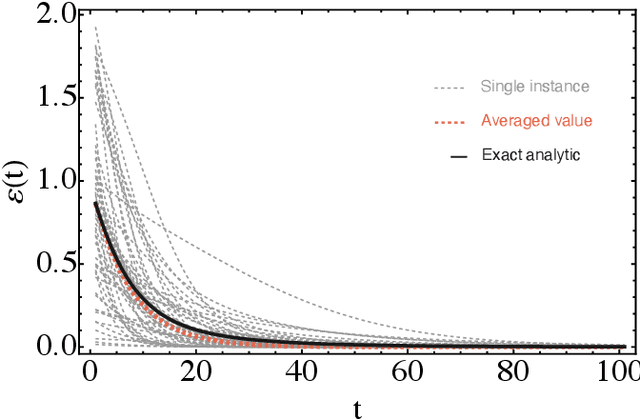
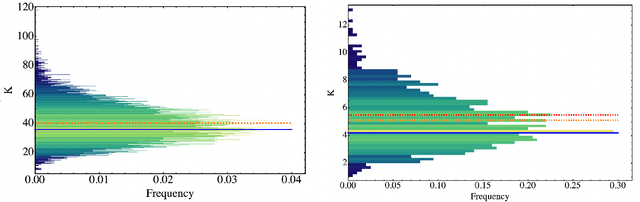
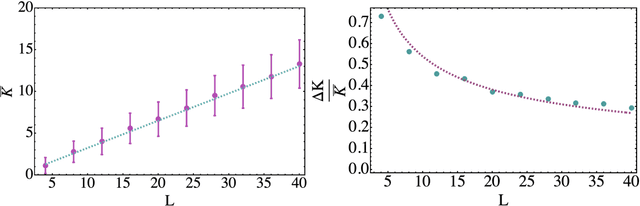
Parametrized quantum circuits can be used as quantum neural networks and have the potential to outperform their classical counterparts when trained for addressing learning problems. To date, much of the results on their performance on practical problems are heuristic in nature. In particular, the convergence rate for the training of quantum neural networks is not fully understood. Here, we analyze the dynamics of gradient descent for the training error of a class of variational quantum machine learning models. We define wide quantum neural networks as parameterized quantum circuits in the limit of a large number of qubits and variational parameters. We then find a simple analytic formula that captures the average behavior of their loss function and discuss the consequences of our findings. For example, for random quantum circuits, we predict and characterize an exponential decay of the residual training error as a function of the parameters of the system. We finally validate our analytic results with numerical experiments.

Generalization in quantum machine learning from few training data

Modern quantum machine learning (QML) methods involve variationally optimizing a parameterized quantum circuit on a training data set, and subsequently making predictions on a testing data set (i.e., generalizing). In this work, we provide a comprehensive study of generalization performance in QML after training on a limited number $N$ of training data points. We show that the generalization error of a quantum machine learning model with $T$ trainable gates scales at worst as $\sqrt{T/N}$. When only $K \ll T$ gates have undergone substantial change in the optimization process, we prove that the generalization error improves to $\sqrt{K / N}$. Our results imply that the compiling of unitaries into a polynomial number of native gates, a crucial application for the quantum computing industry that typically uses exponential-size training data, can be sped up significantly. We also show that classification of quantum states across a phase transition with a quantum convolutional neural network requires only a very small training data set. Other potential applications include learning quantum error correcting codes or quantum dynamical simulation. Our work injects new hope into the field of QML, as good generalization is guaranteed from few training data.

Connecting ansatz expressibility to gradient magnitudes and barren plateaus

Parameterized quantum circuits serve as ans\"{a}tze for solving variational problems and provide a flexible paradigm for programming near-term quantum computers. Ideally, such ans\"{a}tze should be highly expressive so that a close approximation of the desired solution can be accessed. On the other hand, the ansatz must also have sufficiently large gradients to allow for training. Here, we derive a fundamental relationship between these two essential properties: expressibility and trainability. This is done by extending the well established barren plateau phenomenon, which holds for ans\"{a}tze that form exact 2-designs, to arbitrary ans\"{a}tze. Specifically, we calculate the variance in the cost gradient in terms of the expressibility of the ansatz, as measured by its distance from being a 2-design. Our resulting bounds indicate that highly expressive ans\"{a}tze exhibit flatter cost landscapes and therefore will be harder to train. Furthermore, we provide numerics illustrating the effect of expressiblity on gradient scalings, and we discuss the implications for designing strategies to avoid barren plateaus.

Noise-Induced Barren Plateaus in Variational Quantum Algorithms

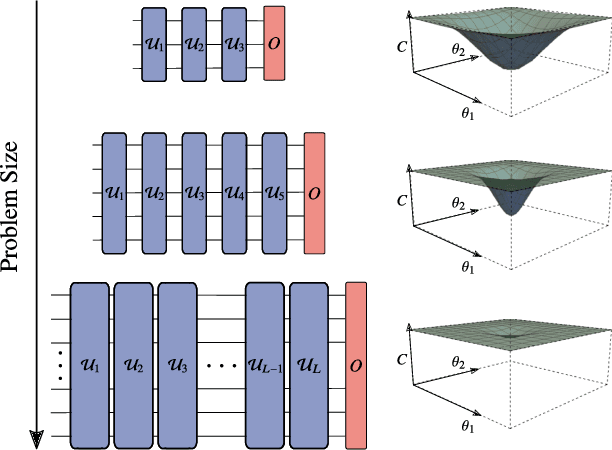
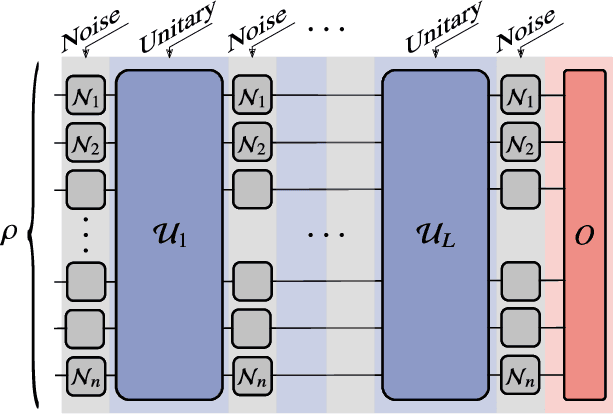
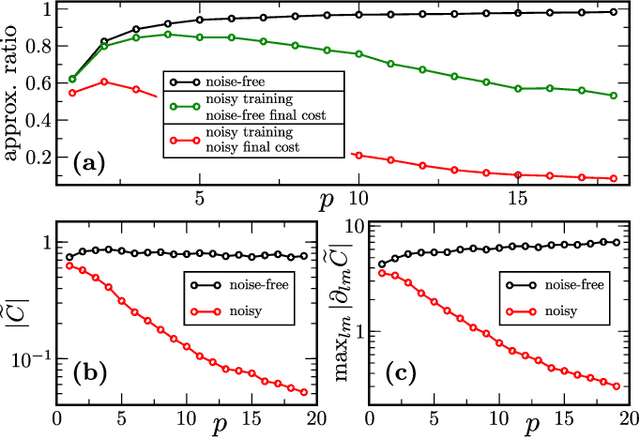
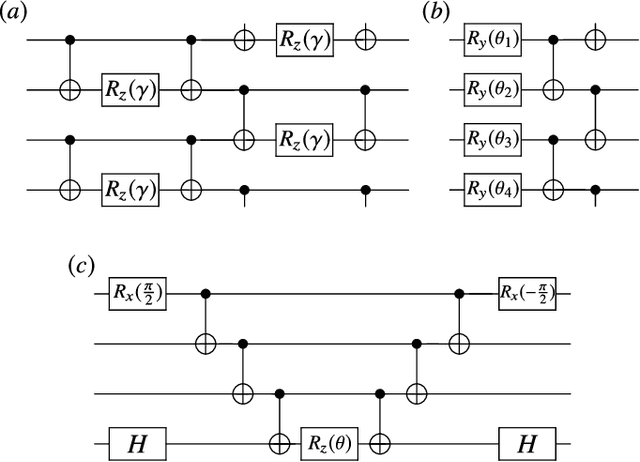
Variational Quantum Algorithms (VQAs) may be a path to quantum advantage on Noisy Intermediate-Scale Quantum (NISQ) computers. A natural question is whether the noise on NISQ devices places any fundamental limitations on the performance of VQAs. In this work, we rigorously prove a serious limitation for noisy VQAs, in that the noise causes the training landscape to have a barren plateau (i.e., vanishing gradient). Specifically, for the local Pauli noise considered, we prove that the gradient vanishes exponentially in the number of layers $L$. This implies exponential decay in the number of qubits $n$ when $L$ scales as $\operatorname{poly}(n)$, for sufficiently large coefficients in the polynomial. These noise-induced barren plateaus (NIBPs) are conceptually different from noise-free barren plateaus, which are linked to random parameter initialization. Our result is formulated for an abstract ansatz that includes as special cases the Quantum Alternating Operator Ansatz (QAOA) and the Unitary Coupled Cluster Ansatz, among others. In the case of the QAOA, we implement numerical heuristics that confirm the NIBP phenomenon for a realistic hardware noise model.

Reformulation of the No-Free-Lunch Theorem for Entangled Data Sets

The No-Free-Lunch (NFL) theorem is a celebrated result in learning theory that limits one's ability to learn a function with a training data set. With the recent rise of quantum machine learning, it is natural to ask whether there is a quantum analog of the NFL theorem, which would restrict a quantum computer's ability to learn a unitary process (the quantum analog of a function) with quantum training data. However, in the quantum setting, the training data can possess entanglement, a strong correlation with no classical analog. In this work, we show that entangled data sets lead to an apparent violation of the (classical) NFL theorem. This motivates a reformulation that accounts for the degree of entanglement in the training set. As our main result, we prove a quantum NFL theorem whereby the fundamental limit on the learnability of a unitary is reduced by entanglement. We employ Rigetti's quantum computer to test both the classical and quantum NFL theorems. Our work establishes that entanglement is a commodity in quantum machine learning.

Trainability of Dissipative Perceptron-Based Quantum Neural Networks

Several architectures have been proposed for quantum neural networks (QNNs), with the goal of efficiently performing machine learning tasks on quantum data. Rigorous scaling results are urgently needed for specific QNN constructions to understand which, if any, will be trainable at a large scale. Here, we analyze the gradient scaling (and hence the trainability) for a recently proposed architecture that we called dissipative QNNs (DQNNs), where the input qubits of each layer are discarded at the layer's output. We find that DQNNs can exhibit barren plateaus, i.e., gradients that vanish exponentially in the number of qubits. Moreover, we provide quantitative bounds on the scaling of the gradient for DQNNs under different conditions, such as different cost functions and circuit depths, and show that trainability is not always guaranteed.