Neuromorphic on-chip reservoir computing with spiking neural network architectures

Reservoir computing is a promising approach for harnessing the computational power of recurrent neural networks while dramatically simplifying training. This paper investigates the application of integrate-and-fire neurons within reservoir computing frameworks for two distinct tasks: capturing chaotic dynamics of the H\'enon map and forecasting the Mackey-Glass time series. Integrate-and-fire neurons can be implemented in low-power neuromorphic architectures such as Intel Loihi. We explore the impact of network topologies created through random interactions on the reservoir's performance. Our study reveals task-specific variations in network effectiveness, highlighting the importance of tailored architectures for distinct computational tasks. To identify optimal network configurations, we employ a meta-learning approach combined with simulated annealing. This method efficiently explores the space of possible network structures, identifying architectures that excel in different scenarios. The resulting networks demonstrate a range of behaviors, showcasing how inherent architectural features influence task-specific capabilities. We study the reservoir computing performance using a custom integrate-and-fire code, Intel's Lava neuromorphic computing software framework, and via an on-chip implementation in Loihi. We conclude with an analysis of the energy performance of the Loihi architecture.

Probabilistic Flux Limiters

The stable numerical integration of shocks in compressible flow simulations relies on the reduction or elimination of Gibbs phenomena (unstable, spurious oscillations). A popular method to virtually eliminate Gibbs oscillations caused by numerical discretization in under-resolved simulations is to use a flux limiter. A wide range of flux limiters has been studied in the literature, with recent interest in their optimization via machine learning methods trained on high-resolution datasets. The common use of flux limiters in numerical codes as plug-and-play blackbox components makes them key targets for design improvement. Moreover, while aleatoric (inherent randomness) and epistemic (lack of knowledge) uncertainty is commonplace in fluid dynamical systems, these effects are generally ignored in the design of flux limiters. Even for deterministic dynamical models, numerical uncertainty is introduced via coarse-graining required by insufficient computational power to solve all scales of motion. Here, we introduce a conceptually distinct type of flux limiter that is designed to handle the effects of randomness in the model and uncertainty in model parameters. This new, {\it probabilistic flux limiter}, learned with high-resolution data, consists of a set of flux limiting functions with associated probabilities, which define the frequencies of selection for their use. Using the example of Burgers' equation, we show that a machine learned, probabilistic flux limiter may be used in a shock capturing code to more accurately capture shock profiles. In particular, we show that our probabilistic flux limiter outperforms standard limiters, and can be successively improved upon (up to a point) by expanding the set of probabilistically chosen flux limiting functions.

Generalization in quantum machine learning from few training data

Modern quantum machine learning (QML) methods involve variationally optimizing a parameterized quantum circuit on a training data set, and subsequently making predictions on a testing data set (i.e., generalizing). In this work, we provide a comprehensive study of generalization performance in QML after training on a limited number $N$ of training data points. We show that the generalization error of a quantum machine learning model with $T$ trainable gates scales at worst as $\sqrt{T/N}$. When only $K \ll T$ gates have undergone substantial change in the optimization process, we prove that the generalization error improves to $\sqrt{K / N}$. Our results imply that the compiling of unitaries into a polynomial number of native gates, a crucial application for the quantum computing industry that typically uses exponential-size training data, can be sped up significantly. We also show that classification of quantum states across a phase transition with a quantum convolutional neural network requires only a very small training data set. Other potential applications include learning quantum error correcting codes or quantum dynamical simulation. Our work injects new hope into the field of QML, as good generalization is guaranteed from few training data.

The Backpropagation Algorithm Implemented on Spiking Neuromorphic Hardware

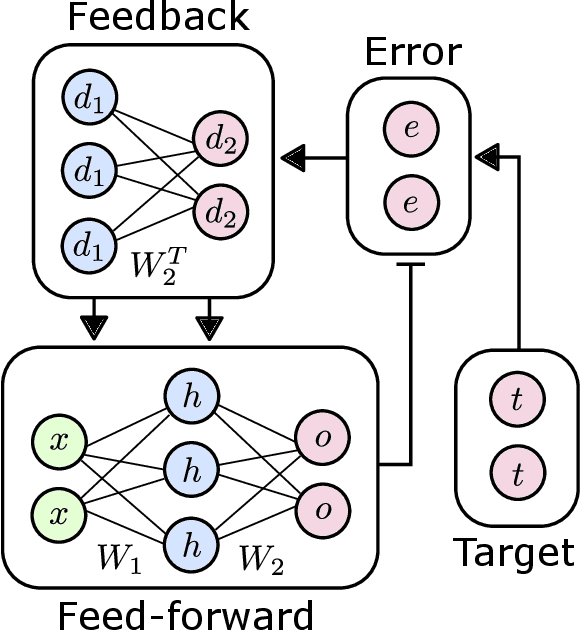
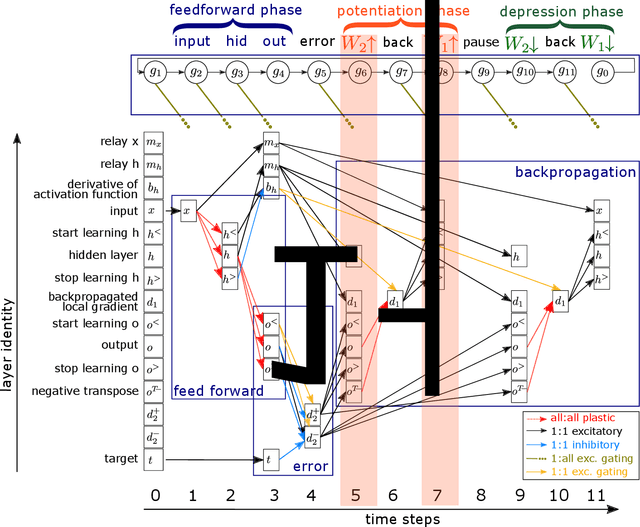
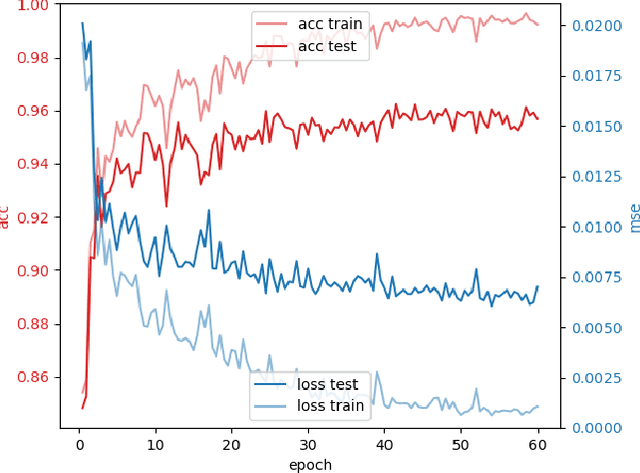
The capabilities of natural neural systems have inspired new generations of machine learning algorithms as well as neuromorphic very large-scale integrated (VLSI) circuits capable of fast, low-power information processing. However, most modern machine learning algorithms are not neurophysiologically plausible and thus are not directly implementable in neuromorphic hardware. In particular, the workhorse of modern deep learning, the backpropagation algorithm, has proven difficult to translate to neuromorphic hardware. In this study, we present a neuromorphic, spiking backpropagation algorithm based on pulse-gated dynamical information coordination and processing, implemented on Intel's Loihi neuromorphic research processor. We demonstrate a proof-of-principle three-layer circuit that learns to classify digits from the MNIST dataset. This implementation shows a path for using massively parallel, low-power, low-latency neuromorphic processors in modern deep learning applications.

Long-time simulations with high fidelity on quantum hardware

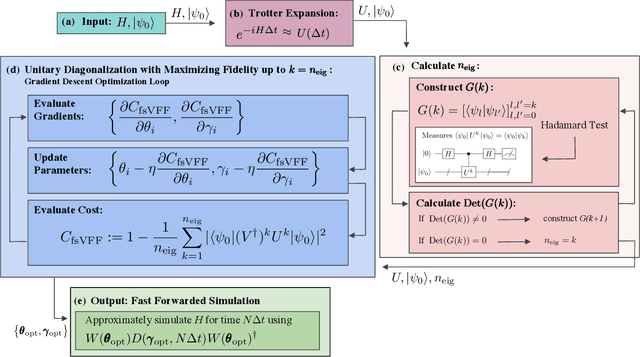
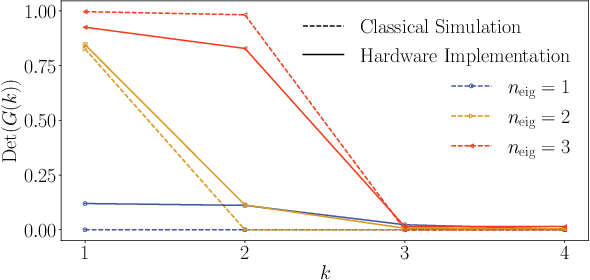
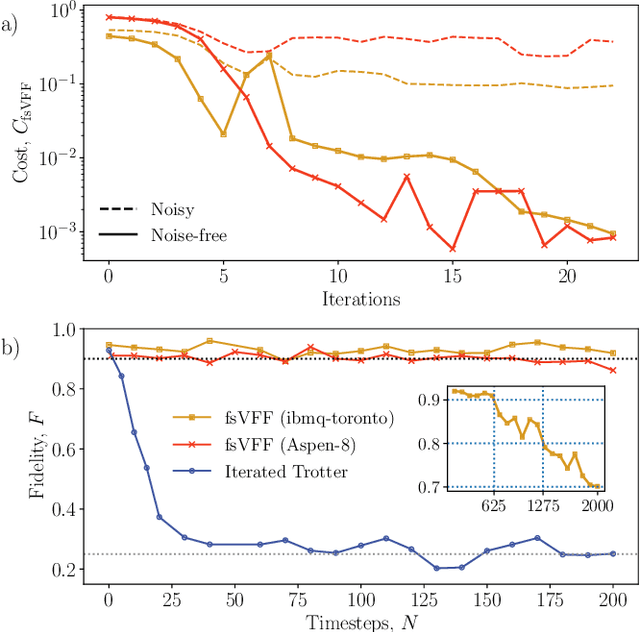
Moderate-size quantum computers are now publicly accessible over the cloud, opening the exciting possibility of performing dynamical simulations of quantum systems. However, while rapidly improving, these devices have short coherence times, limiting the depth of algorithms that may be successfully implemented. Here we demonstrate that, despite these limitations, it is possible to implement long-time, high fidelity simulations on current hardware. Specifically, we simulate an XY-model spin chain on the Rigetti and IBM quantum computers, maintaining a fidelity of at least 0.9 for over 600 time steps. This is a factor of 150 longer than is possible using the iterated Trotter method. Our simulations are performed using a new algorithm that we call the fixed state Variational Fast Forwarding (fsVFF) algorithm. This algorithm decreases the circuit depth and width required for a quantum simulation by finding an approximate diagonalization of a short time evolution unitary. Crucially, fsVFF only requires finding a diagonalization on the subspace spanned by the initial state, rather than on the total Hilbert space as with previous methods, substantially reducing the required resources.

Reformulation of the No-Free-Lunch Theorem for Entangled Data Sets

The No-Free-Lunch (NFL) theorem is a celebrated result in learning theory that limits one's ability to learn a function with a training data set. With the recent rise of quantum machine learning, it is natural to ask whether there is a quantum analog of the NFL theorem, which would restrict a quantum computer's ability to learn a unitary process (the quantum analog of a function) with quantum training data. However, in the quantum setting, the training data can possess entanglement, a strong correlation with no classical analog. In this work, we show that entangled data sets lead to an apparent violation of the (classical) NFL theorem. This motivates a reformulation that accounts for the degree of entanglement in the training set. As our main result, we prove a quantum NFL theorem whereby the fundamental limit on the learnability of a unitary is reduced by entanglement. We employ Rigetti's quantum computer to test both the classical and quantum NFL theorems. Our work establishes that entanglement is a commodity in quantum machine learning.